基于分布水动压力的飞行器水下载荷计算方法研究
刘文一,李玉龙,吴训涛
(中国人民解放军91550部队41分队,大连,116023)
0 引 言
飞行器水下垂直向上运动时,由于空泡的出现,会经受复杂的水下载荷,在飞行器表面布置压强传感器来测量表面压强,由于受传感器安装位置和采样频率的限制,测得的压强数据在时间和空间上是离散的。为了对飞行器进行动力学响应分析,必须将离散的数据连续化,才能获得飞行器的载荷分布情况[1]。
获得飞行器表面压强场后,将表面压强场加载在飞行器表面上进动力学响应分析,以获得飞行器对表面压强的动响应,从而辨识得到飞行器的内力,即飞行器各截面随时间和空间变化的轴向力、剪切力和弯矩[2]。对于长径比较大的飞行器,剪切力和弯矩是其水下载荷的主要部分,这两个值直接影响飞行能否正常出水和出水姿态,因此辨识得到的飞行器水下载荷具有重要的工程应用价值[3]。
1 表面压强
对于飞行器水下载荷分析而言,主要关心飞行器截面分布法向力。实验时在飞行器表面布置若干个压强测点,然后对测得的表面压强进行插值求得飞行器连续表面压强场。飞行器在出水过程中法向力分布会出现一个峰值,而且峰值并不在一个固定的部位,瞬时出现法向力峰值的主要原因是由于空泡产生了倾斜。对于同一截面,当迎水面处于空泡末端高压作用时,与其对应的背水面已经进入空泡低压区,形成较大的迎、背水压差,因此产生了较大的瞬时截面分布法向力峰值。同时,在出水过程中,随着速度增加,空泡数随之降低,空泡末端涡旋回射产生的压强峰逐渐后移,由此引起的法向力分布峰值也逐渐后移[4]。
飞行器在水下任一点的表面压强可表示为

式中 CP为压强系数;ρ为水的密度,kg/m2;V∞为飞行器运动速度,m/s;P0为环境压强,Pa。
由于飞行器在水下会产生空化现象,因此载荷计算关心的是CP为负值的部分,引入符号ζ:


2 连续压强场
飞行器体表面压强测量数据测得了每个测点上压强随时间的变化历程,但对于两个测点之间的压强分布,则必须对压强测量数据进行连续化处理,利用波形插值法可以将离散的压强数据插值得到随时间变化的压强场,这是因为在出水过程中,空泡沿飞行器表面是按照一定速度推进溃灭的[5]。
进行波形插值时,为确定某点的压强载荷,首先根据其位置确定出水时刻,移动时间轴,将出水时刻的主波峰对齐,然后进行线性插值得到峰值附近的压强曲线;最后还原时间轴,得到该点的压强载荷时间历程曲线[6],如图1所示。
由于飞行器发射时有艇速存在,使飞行器迎水面
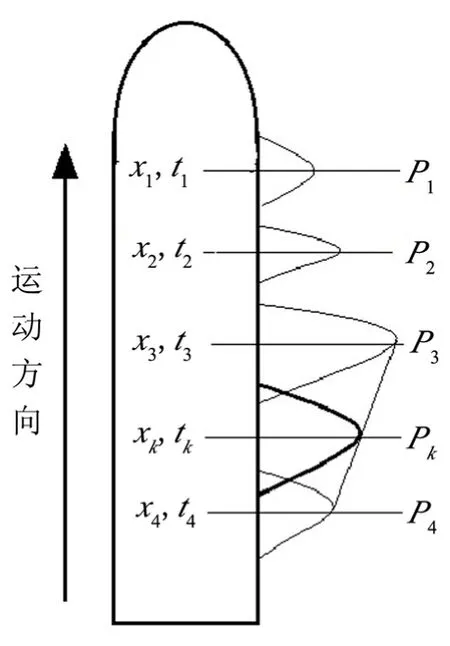
图1 飞行器轴向表面压强插值原理Fig.1 Principle of Axial Surface Pressure Interpolation for Aircraft P1~P4—实测压强数据;PK—插值得到的压强数据;xk,tk—测点位置和出水时刻
根据水动压强测压点相对位置信息与飞行器结构外形,建立柱坐标系,利用柱坐标描述测压点的位置。将迎水面和背水面测压点坐标存成一个文件,作为坐标输入。对迎水面和背水面测压点对应的实验数据进行预处理,与弹道合并作为数据文件。水动压强载荷输入数据预处理流程如图2所示,从而到飞行器表面随时间和空间变化的连续压强场,如图3所示。和背水面存在压强差,因此同一截面迎水面和背水面压强的分布和大小不同,对于周向压强场,则采用余弦理论插值得到。

图2 水动压强载荷数据预处理流程Fig.2 Preprocessing Flow of Hydrodynamic Pressure Load Date

图3 飞行器表面时间-空间连续压强场Fig.3 Time-space Continuous Surface Pressure Field of Aircraft
3 飞行器动响应分析
3.1 飞行器质量分布
载荷计算时的一个基本的定义是对广义动能起作用的任何项必须在质量矩阵中创建一个系数。另一个定义是任何广义力 F与加速度项成比例,就产生了质量矩阵M,即:

其中,加速度矢量u˙˙的每一个分量代表一个广义自由度[7]。
载荷计算时,将飞行器简化为六自由度变质量-变刚度梁模型,梁弯曲振动的单元质量矩阵 me可按如下公式计算:
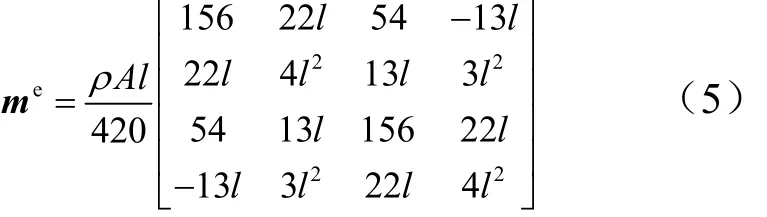
式中 A为梁截面积;l为单元长度。
对于质量矩阵,在实际工程计算中,根据情况也可以把各节点分得的集中质量直接填入总质量对应位置[8]。集中转动惯量按下式计算:

式中 me为该站上的集中质量;R为飞行器半径;h为处于梁端点时与相邻点间距之半;处于中间点时取它相邻的前后两点距离之半[9]。
对于集中质量的弹性梁,其广义质量为

式中 Mj为第j个模态的广义质量;mi为第i站的集中质量。
3.2 飞行器刚度分布
飞行器简化成梁时,平衡方程为

式中eωP为功等效力;u为位移矩阵;P为压力矩阵;Q为剪切力矩阵;eK为梁单元的刚度矩阵,即:

计算导数并积分后可得到梁的刚度矩阵为

式中 E为材料的弹性模量;G为材料的剪切模量。
3.3 飞行器有限元模型
通过飞行器的质量和刚度分布特性可建立飞行器有限元模型。由于飞行器长径比较大,而且沿飞行器轴向各部段的刚度和质量质心是变化的,因此计算时需建立飞行器的变质量-变刚度梁模型。梁单元的等效截面积为0.5 m2,转动惯量IZZ为1 kg·m2。离散单元为 2节点六自由度无质量欧拉梁单元,质量按集中质量处理,建立的飞行器变质量-变刚度有限元模型如图4所示。
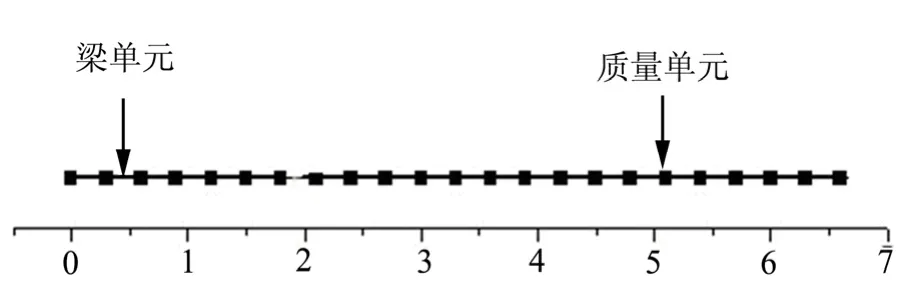
图4 飞行器变质量-变刚度有限元模型Fig.4 Mass-variable and Stiffness-variable Beam Element Model of Aircraft
3.4 飞行器动响应计算
作用在飞行器表面的力有纵向力和横向力,根据纵向力分布系数和横向力分布系数等参数,通过波形插值和余弦插值可以得到飞行器水下运动过程中作用在飞行器节点上的纵向外力场和横向外力场,从而采用Newmark提出的逐步积分法进行结构分析。对飞行器整个水下运动过程利用动力学分析软件进行瞬态动力学分析,从而计算得到飞行器各截面在水下运动过程中随时间变化的力矩M和剪切力f。
对于一个n维自由度的振动系统,其动力学方程为

式中 M,C和K分别为系统质量、阻尼和刚度矩阵;{˙x},{x˙},{x}和{f}分别为加速度、速度、位移和激励力向量[10]。
其特征方程为

其中,特征值所对应的特征向量{ϕr}是正交的,同时{ϕr}对刚度矩阵K及质量矩阵M也是正交的,即:

为将物理坐标表示的动力学方程(13)解耦,须将其转换到模态坐标系。
通过以上变换,原来耦合的动力学方程式就成为解耦的以模态坐标表示的模态方程:

通过求解式(16)表示的 N个独立的模态坐标下的动力学方程,可得到模态坐标下的各阶模态坐标向量 {ηr( t)},将其代入式(14)便可得系统在物理坐标系下的位移响应{x},将其加载在有限元模型上进行动力学响应分析,进而可求得系统的各截面随时间变化的弯矩和剪切力,结果如图5和图6所示。

图5 飞行器某截面处的弯矩曲线Fig.5 Bending Moment at a Section of the Aircraft

图6 飞行器某截面处的剪切力曲线Fig.6 Shear Force at a Section of the Aircraft
4 结 论
a)对于轴向离散的表面压强,可采用波形插值法插值,可得到计算所需轴向的时间连续压强场;对于周向压强场,则利用余弦理论插值得到。
b)将迎水面和背水面测压点坐标合并、表面压强测点的实验数据预处理后与弹道合并,作为坐标和载荷的输入值;再进行编程计算,得到飞行器表面随时间和空间变化的连续压强场。
c)对于大质量变刚度的飞行器,可根据其质量-刚度分布特征,可建立变刚度-变质量的梁模型代替三维模型进行动力学响应分析。
d)将插值得到的随时间和空间变化的表面压强场,加载到飞行器有限元模型上进行动力学响应分析,可得到飞行器各截面随时间变化的弯矩、剪切力,其结果对于发射条件选择和飞行器结构设计具有重要的参考价值。

