子弹稳定装置翼片动态张开过程研究
陈佩银,杨永刚,薛再清,张韩宇
(北京航天长征飞行器研究所,北京,100076)
0 引 言
尾翼稳定装置是子弹的重要部件,在子弹飞行中产生阻力,使子弹收敛到良好的飞行稳定性。子母弹在高空抛撒后子弹离开子弹舱,稳定装置的翼片在高空气流压力和初始力等综合作用下张开,张开到位后与稳定装置的尾翼座发生猛烈碰撞,故要求子弹稳定装置有一定的飞行强度和刚度,确保翼片张开到位时碰撞冲击力作用下的结构完好性和子弹飞行姿态收敛稳定。因此子弹翼片动态张开过程的正确描述及飞行强度计算对子弹设计具有重要意义[1]。
由于测试条件受限,高空高速运动中的子弹翼片动态张开过程无法真实测到,只能通过各种分析手段来定性分析。很多研究在开展子弹稳定装置飞行强度计算时忽略真实的动态张开过程,采用将空气动力静态加载到翼片的方式来计算飞行强度[2]。任宪仁[3]应用了空气动力学算法并借助仿真软件,对尾翼结构在膛口流场中所受的气体动力学载荷进行分析,虽然取得了较好的研究进展,但由于激波参数的突跃性质,使得数值计算精度不高,而细分和重分网格又带来了巨大的计算量并引入了复杂的算法问题,难以获得令人满意的结果。文献[1]、[4]、[5]采用常规的空气阻力计算方法来开展翼片动力学分析,未考虑翼片张开角度不同时高速气流的绕流等现象。
本文力图以简单的方法,为子弹药稳定装置设计者提供一种翼片动态张开工程计算方法。该方法将空气近似为理想气体,其迎风面压力计算采用斜激波理论公式,背风面压力计算采用普朗特-梅耶膨胀波理论公式,根据翼片受力情况建立翼片张开的动力学数学模型。这种算法简单实用,可以同时给出翼片气动力和动态张开过程,能够较准确地模拟翼片在一定初始条件下的运动,最后采用该算法分析不同攻角和角速度对子弹翼片动态张开过程的影响,并就其对工程设计的影响进行定性讨论,可为子弹稳定装置优化设计及其飞行强度计算提供技术支持。
1 子弹稳定装置翼片张开动态过程描述
子母弹在高空抛撒后给子弹一定的初始角速度和径向速度,子弹离开子弹舱,子弹稳定装置的约束解除,在母弹较高的牵连速度等各种因素条件下,高空高速运动中子弹稳定装置的翼片动态张开过程受力非常复杂,张开到位后与尾翼座碰撞,翼片受到强大冲击力。对这一系列过程开展动力学计算,需要先描述翼片张开过程的受力情况。
本文主要针对弹簧抗力后张式尾翼展开分析,该类型尾翼包括尾翼座、翼片、轴、翼片簧和销等。抛撒时,翼片由翼片簧提供初始动力,在高速气流气动力共同作用下张开至后掠角,如图1所示。
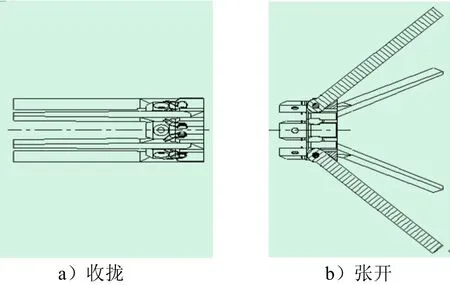
图1 尾翼稳定装置示意Fig.1 Projectile Stabilizing Device
1.1 翼片张开受力情况分析
子弹稳定装置的翼片张开过程如图2所示,设翼片相对于弹轴的张开角为α,张开过程中α由0°逐渐增大到最大设计值135°。翼片张开过程中受到多个力的综合作用,包括翼片簧的扭力矩 Ms、迎风面气体压力py、背风面气体压力 pb( py和 pb综合作用为气动力)、重力和约束反力等。约束反力可分为垂直于运动副元素表面的法向反力和切于运动副元素表面的摩擦力[3]。重力和约束反力相对于气动力对翼片转动影响很小,动力学计算时可忽略不计。因此,本文在翼片动态张开过程中主要考虑翼片簧的扭力矩和气动力,如图3所示。


图3 翼片张开过程受力情况示意Fig.3 Force in Opening Process of Projectile Stabilizing Device
翼片动态张开后,最后以一定的角速度张开到位后将与座体发生碰撞。翼片簧的扭力矩为翼片提供初始张开条件。将空气近似为理想气体,其迎风面压力计算采用斜激波理论公式,背风面压力计算采用普朗特-梅耶膨胀波理论公式[6]。
1.1.1 迎风面气体压力计算方法
当超声速来流遇到翼片斜面后,会产生一个斜激波,同时气流方向发生转折,如图4所示。

图4 迎风面气流和斜激波示意Fig.4 Head-on Airflow and Oblique Shock Wave Ma—来流马赫数;Mah—激波后气流的当地马赫数;θ—气流转折角;φ—激波角;O—翼片与子弹的交点;OO'—激波面方向
根据斜激波理论,二者关系为

当h1Ma<时(此时θ大于临界值maxθ),脱体激波形成,如图5所示。

图5 翼片脱体激波形成示意Fig.5 Development of Detached Shock Wave
脱体激波形成后,翼片迎风面各处压力随该点与波阵面距离不同而变化,用解析方法计算十分困难。因此本文作工程简化,假定脱体激波形成后气体迎风面压力保持不变,保持上一时刻的气体压力。翼片张开角α在( θmax,18 0 -θmax)范围内均属于该类情况。
1.1.2 背风面压力计算方法
当超声速来流遇到翼片背风面时,会产生多道膨胀波并使气流方向发生转折,如图6所示。

图6 背风面气流转折示意Fig.6 Transition Diagram of Leeward Airflow
根据普朗特-梅耶膨胀波理论,θ与马赫数的关系为

式中2Ma为经膨胀波转折后的气流马赫数; k为气体比热比;bp为背风面压力; *p为来流总压。气流转折角θ等于翼片张开角α,当翼片张开角α≥90°时可将背风面气体压力忽略不计。
1.2 翼片张开动力学分析
根据子弹稳定装置的翼片受力情况分析,翼片绕轴转动按照牛顿定律计算,其角加速度的绝对值为

式中 ω为翼片角速度(本文定义翼片张开方向为正); MI为翼片所受的综合力矩(相对于转轴);I为翼片转动惯量;t为张开时间。
根据上述翼片受力情况分析,翼片所受的综合力矩 MI为
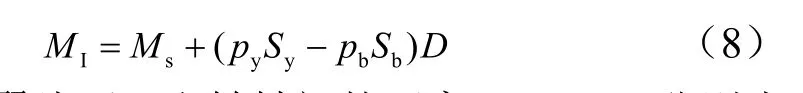
式中 D为翼片压心和转轴间的距离; Sy, Sb分别为翼片迎风面积和背风面积; pySy- pbSb为总气动力。若质心与压心重合,则与质心和转轴间的距离 Xc相等,即D = Xc。翼片簧作用在翼片上,其扭力矩为 Ms。
综合式(7)和式(8),可得到翼片转动张开的动力学方程:
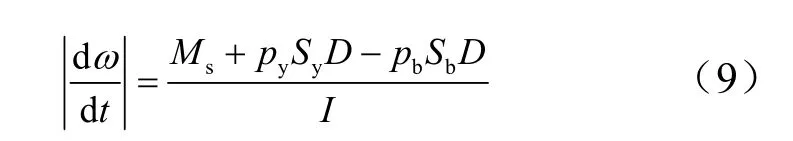
翼片初始角度和角速度均为0,需要的参数有翼片簧的扭力矩、翼片的质量参数、翼片迎风面和背风面的气体压力。在上述建立的数学模型中,代入相关已知参数的数值,在计算机上用 MATLAB中的龙格-库塔库函数对建立的微分方程进行编程计算,即可计算得到不同时刻翼片的角加速度、角速度、张开角,以及总张开时间。
抛撒赋予子弹一定的初始角速度和径向速度,本文动力学计算中,先不考虑子弹的径向速度,分析一定初始角速度和初始攻角对翼片张开过程的影响。
翼片动态张开后,最后以一定的角速度张开到位,以一定速度与尾翼座发生碰撞。后续可根据此碰撞速度进行翼片和尾翼座的碰撞强度计算,从而得出尾翼飞行强度是否满足要求的结论,是否需要对翼片和尾翼座进行优化设计。
2 某子弹稳定装置翼片动态张开算例
本文计算某子弹抛撒后稳定装置翼片的动态张开过程。某子母战斗部抛撒时母弹速度为750 m/s,当地大气压力为80 253 Pa,翼片质心和压心重合。在本文动力学计算中,先不考虑子弹抛撒后的初始角速度和径向速度。翼片初始角度和角速度均为0,翼片簧的扭矩为翼片提供初始张开条件,在空气来流作用下张开运动。翼片簧扭力矩为 Ms=0.7 ×(170 - α),初始时为119 N·mm,翼片张开到位时为24.5 N·mm。
以钛合金翼片为例,已知:翼片质量m=24.4 g,迎风面积yS=600 mm2,质心和转轴间的距离D=Xc=48.3 mm,翼片转动惯量I=87.0 kg·mm2,时间步长为10 μs。动态张开过程计算结果如图7~11所示。

图7 翼片簧扭力矩曲线Fig.7 Torsional Moment Curve of Fins Spring

图8 翼片迎风面和背风面压力曲线Fig.8 Pressure Curve of Empennage in the Head-on and Leeward Surface

图9 翼片张开角加速度曲线Fig.9 Angular Acceleration Curve of Empennage Opening

图10 翼片张开角速度曲线Fig.10 Angular Velocity Curve of Empennage

图11 翼片张开角度随时间变化曲线Fig.11 Changing Curve of the Opening Angle of Empennage
计算表明,在11.20 ms时,迎风面形成脱体激波,此时气流转折角maxθ=24.4°。此时假定脱体激波形成后气体迎风面压力保持不变,保持上一时刻的气体压力。翼片张开角α在24.4°~135°的范围内均属于该类情况。在14.2 ms时,翼片张开到垂直α=90°。在15.4 ms时,翼片完全张开α=135°,此时角加速度为6.53×106(°)/s2,角速度为 3.90×104(°)/s。
为说明子弹飞行过程中气动力对稳定装置的影响,特计算了静态条件下翼片动态张开过程。计算结果如图12~14所示。翼片簧的扭矩为翼片提供初始张开条件,在15.4 ms时,翼片才张开α=9°;在50.3 ms时,翼片张开到垂直α=90°;在63.5 ms时,翼片完全张开α=135°,此时角加速度为1.62×104(°)/s2,角速度为 3570 (°)/s。翼片张开时间与静态下实测数据较一致。对比结果表明,在有气动力的情况下,翼片张开更迅速。
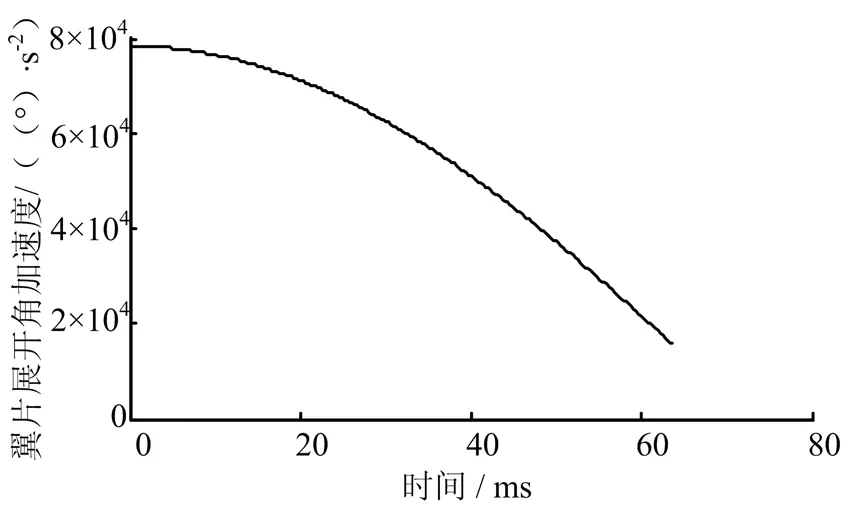
图12 翼片张开角加速度曲线Fig.12 Angular Acceleration Curve of Empennage Opening

图13 翼片张开角速度曲线Fig.13 Angular Velocity Curve of Empennage
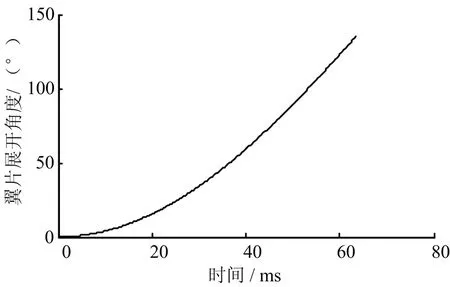
图14 翼片张开角度随时间变化曲线Fig.14 Changing Curve of the Opening Angle of Empennage
由图 13可知,子弹张开到位时的角速度ω=3.90×104(°)/s,翼片质心线速度cvXω=⋅=32.8 m/s。根据此计算结果进行翼片和尾翼座强度计算。
3 子弹攻角和角速度对翼片张开过程的影响
当子弹飞行初始时刻存在攻角β或有角速度Dω时,位于迎风面处的翼片(内侧的翼片)最难张开,此处是翼片张开关注的重点。本节计算攻角为0°~3°、角速度为0~1000 (°)/s时内侧翼片的动态张开情况,并作简要分析。
3.1 子弹攻角对翼片动态张开的影响
子弹初始速度为750 m/s,当地大气压力80 253 Pa时,翼片质心和压心重合。本节计算β为0°~3°时内侧翼片的动态张开情况。
在很小攻角的情况下,子弹迎风面翼片在张开初始阶段(张开角小于攻角时),翼片受到的总气动力与翼片簧扭力方向相反,会阻碍翼片的张开,导致翼片张开初始阶段非常缓慢。当翼片的张开角大于攻角时,翼片受到的总气动力与翼片簧扭力方向相同,此时与无攻角状态的翼片张开情况相同。
计算结果如图15~18所示。从图15~18可以看出,攻角越大,翼片张开越缓慢。当β超过0.8°时翼片气动力矩开始超过翼片簧提供的初始扭力矩,翼片已经无法张开。由此可见,当子弹抛撒有攻角时,其翼片张开过程相对困难。子弹攻角对迎风面翼片的张开存在明显的不利影响,翼片的张开速度明显减小。可见在进行子弹稳定装置设计时必须考虑攻角的影响。
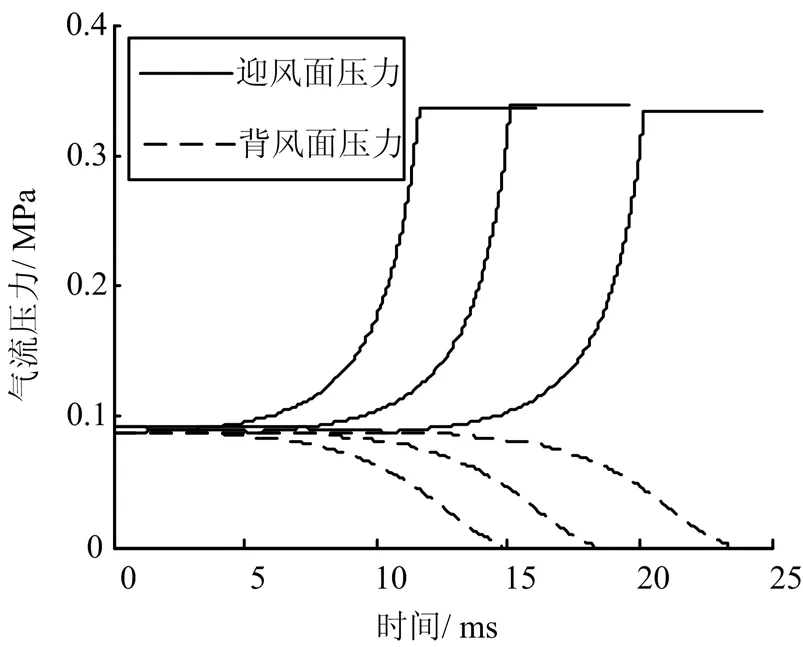
图15 有攻角时翼片迎风面和背风面压力曲线(3种不同攻角:左0°、中 0.5°、右0.7°)Fig.15 Pressure Curve of Empennage in the Head-on and Leeward Surface (Attack Angle:0°、0.5°、0.7°)

图16 有攻角时翼片张开角加速度曲线Fig.16 Angular Acceleration Curve of Empennage Opening

图17 有攻角时翼片张开角速度曲线Fig.17 Angular Velocity Curve of Empennage
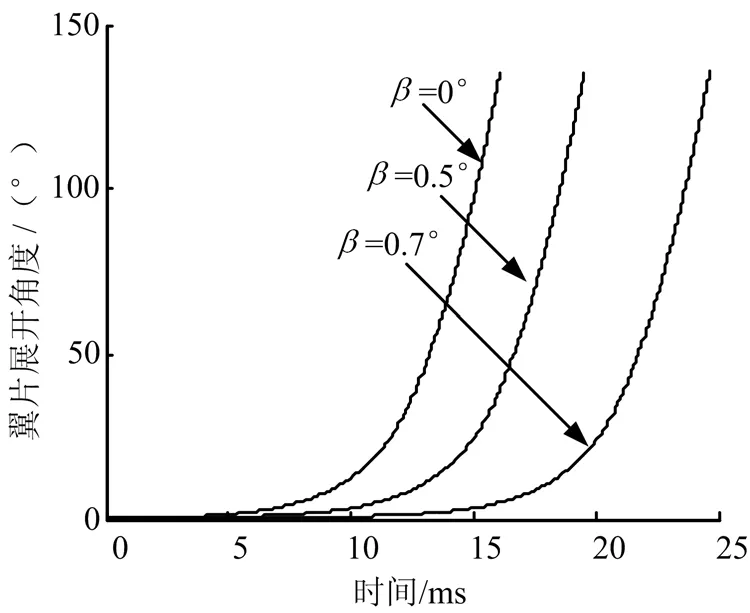
图18 有攻角时翼片张开角度随时间变化曲线Fig.18 Changing Curve of the Opening Angle of Empennage
3.2 子弹角速度对翼片动态过程的影响分析
本节计算子弹角速度Dω为0~1000 (°)/s时内侧翼片的动态张开情况。其余计算初始条件同上。
子弹在很小角速度条件下,翼片张开方向与角速度方向相同的翼片存在初始正角速度,极有利于翼片张开。而翼片张开方向与角速度方向相反的翼片即存在初始负角速度,它的影响同攻角对迎风面翼片的影响相同,会阻碍翼片的张开,导致翼片张开初始阶段非常缓慢。
计算表明:角速度越大,与角速度方向相反的翼片张开越缓慢,如图19~22所示。角速度的影响比攻角影响更大,当角速度超过243 (°)/s时翼片已经无法张开。
从图19和图22可以看出,子弹角速度对相反方向的翼片的张开存在明显的不利影响,翼片的张开速度明显减小。可见在进行子弹稳定装置设计时必须考虑角速度的影响。
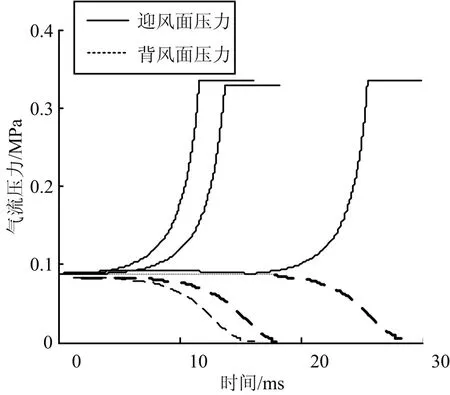
图19 有角速度时翼片迎风面和背风面压力曲线(3种不同角速度:左0(°)/s、中 120(°)/s、右240(°)/s)Fig.19 Pressure Curve of Empennage in the Head-on and Leeward Surface(3 different angle velocity:0(°)/s、120(°)/s、240(°)/s)

图20 有角速度时翼片张开角加速度曲线Fig.20 Angular Acceleration Curve of Empennage Opening

图21 有角速度时翼片张开角速度曲线Fig.21 Angular Velocity Curve of Empennage
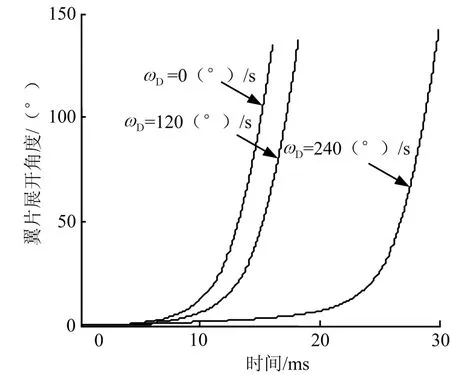
图22 有角速度时翼片张开角度随时间变化曲线Fig.22 Changing Curve of the Opening Angle of Empennage
4 结束语
本文为子弹药稳定装置设计者提供一种翼片动态张开工程计算方法,可同时给出翼片迎风面和背风面的气动力,以及翼片张开动态过程,可较准确地模拟翼片在一定初始条件下的运动。通过计算并分析某子弹稳定装置翼片的张开运动特点,验证了计算方法的可行性,并就初始攻角和初始角速度及其对工程应用的影响进行定性讨论。

