考虑全局投标者后悔心理行为的组合拍卖的投标均衡策略
高广鑫, 樊治平, 尤天慧, 郭娅舒
(1.南京航空航天大学 经济与管理学院,江苏 南京 211106; 2. 东北大学 工商管理学院,辽宁 沈阳 110167)
0 引言
组合拍卖是指投标者可以对多个拍卖物品的任何一个组合进行投标,也可以同时对几个组合进行投标的拍卖形式[1]。组合拍卖主要应用于存在互补性或替代性关系的物品的交易[2,3],例如无线电频谱拍卖[4,5]、网上集中采购拍卖[6]、机场跑道空位拍卖[7]、航班地面等待时隙分配[8]和网页广告位拍卖[9]等。与其他拍卖机制相比,组合拍卖可以使得投标者灵活地表达其对拍卖物品间互补性或替代性的偏好,降低投标者风险,增加卖方收益,从而提高拍卖效率[2]。许多实验研究表明[10~15],一级价格密封式拍卖过程中投标者往往会表现出预期后悔心理行为,并且投标者的预期后悔心理行为将会对其投标策略产生影响。但是,以往研究成果大多是针对单物品拍卖研究考虑投标者后悔心理行为的投标均衡策略[10~11,15,16],而针对多物品组合拍卖情形的研究较少关注。因此,在已有研究的基础上,有必要针对考虑投标者后悔心理行为的组合拍卖的投标均衡策略进行深入研究,这有助于投标者针对组合拍卖进行科学投标决策。
目前,针对考虑投标者后悔心理行为的组合拍卖的投标均衡策略的研究尚不多见,但可以看到一些相关的研究成果[10~18]。例如:Engelbrecht-Wiggans[10]针对一级价格密封式单物品拍卖中投标者的最优投标策略问题进行了研究,他指出使得投标者期望效用最大化的投标策略不仅依赖于其期望的货币收入,也依赖于多种形式的后悔情感,同时对拍卖中的超投标现象做出了解释;Engelbrecht-Wiggans和Katok[11]针对一级价格密封式单物品拍卖的最优投标策略确定问题的研究,在独立私人估价模型的基础上,构建了考虑投标者后悔行为的期望效用函数,并通过分析确定了最优投标策略,从而解释了观测到的超投标现象;Fishman和Durham[12]针对拍卖中投标者后悔情感对投标策略的影响,通过利用与后悔情感相关的反馈信息作为变化的实验条件,测试了投标者后悔情感对投标策略的影响,并对均衡投标结果进行了预测分析;Filiz和Ozbay[13]针对单物品拍卖中失败者后悔情感对于投标策略的影响进行了研究,研究结果表明:投标者预期的失败者后悔是产生超投标现象的主要原因,而在竞标获胜的情形下,投标者一般不会预期后悔,并且不会出现明显的低投标现象;Du等[14]针对拍卖中投标者预期后悔对投标策略的影响,通过实验方法研究了投标过程中预期后悔与实际经历的后悔之间的误差,并得到预期后悔大于实际经历的后悔的结论;Engelbrecht-Wiggans和Katok[15]针对一级价格密封式拍卖中与后悔情感相关的反馈信息对投标行为的影响进行了研究,他们指出在拍卖中可能存在两种投标者后悔情感,即获胜者后悔和失败者后悔,通常情况下,投标者对于获胜者后悔敏感时会降低平均投标价,而当投标者对于失败者后悔更敏感时便会提高平均投标价,并通过实验验证了这个结论;在已有研究基础上,他们还通过改变后悔反馈信息将投标者后悔行为和损失规避行为区别开来,进行了相应的实验研究和理论分析[17],分别测试了两种行为对于投标策略的影响,并指出相对于损失规避来说投标者后悔对于投标行为的影响更大;Astor等[18]针对一级价格密封式拍卖中投标者的获胜者后悔和失败者后悔情感,通过心理学实验操纵投标者情感进程,验证了文献[15]中不同类型的后悔参数的准确性。
综上,已有研究对考虑投标者后悔心理行为的单物品拍卖的投标策略研究做出了重要贡献,需要指出的是,在现实中,组合拍卖作为单物品拍卖的一种扩充得到了广泛应用[2],但已有研究没有针对考虑投标者后悔心理行为组合拍卖的投标策略进行深入研究。因此,在已有研究的基础上,进一步研究考虑投标者后悔心理行为的组合拍卖的投标均衡策略问题是有必要的。鉴于此,本文则是针对考虑投标者后悔心理行为的组合拍卖的投标均衡策略问题,在全局投标者存在预期后悔心理行为的假设下,在文献[10]和[15]采用线性后悔函数来刻画投标者后悔心理行为的基础上,构建组合拍卖模型,并分析全局投标者投标均衡策略需要满足的充分和必要条件。进一步地,依据构建的模型,通过数值实验,分析局部投标者人数、组合效应系数和全局投标者后悔参数对全局投标者投标均衡策略的影响。最后,通过一个关于无线电频谱组合拍卖的算例说明本文给出的模型及投标均衡策略分析方法的潜在应用。
1 问题描述与符号说明
考虑拍卖者要采用组合拍卖的方式同时出售两个异质互补性物品(A和B),假定在拍卖中存在两类投标者同时参与竞标,其中第一类投标者(以下称作局部投标者)只对两个拍卖物品中的某一个感兴趣,他们中会有一部分投标者仅对物品A进行投标,而另一部分投标者仅对物品B进行投标,且局部投标者之间是相互对称的,也就是说,他们对每个物品的估价在某一区间内均服从同一概率分布;而第二类投标者(以下称作全局投标者)对提供的两个物品都感兴趣,他们会针对物品A和B的组合进行投标,且若其同时赢得两个物品,那么其所获得的效用大于分别赢得两个物品中任意一个的效用之和,也就是说全局投标者同时赢得两个物品时将获得组合效应α,α>0。在拍卖过程中,每个投标者仅有一次投标机会,且拍卖结束后,每个投标者不仅会得知自身获胜状态而且还会知道拍卖的最终获胜价。
基于上述描述,考虑全局投标者在投标前存在预期后悔心理行为[13,15],具体描述如下:
若投标者预期投标失败,且获胜价不高于其支付意愿,则意味着该投标者错过了一个能以合适的价格水平获胜的机会,而实际上这个价格只要比获胜价高最小单位数量即可,此时该投标者会因为错失一个良好的获胜机会而产生后悔预期,进而在实际拍卖中,会适当地提高自己的投标价格水平来赢得拍卖物品。
显然,影响全局投标者事前期望效用的因素体现在两个方面:一个是投标者预期投标获胜的期望收益;另一个是投标者预期投标失败的后悔感知效用。本文要解决的问题是在考虑影响投标者事前期望效用的因素的情况下,针对全局投标者,如何构建考虑投标者后悔心理行为的组合拍卖模型,并分析其投标均衡策略。
为了便于下文分析,本文涉及的相关符号及变量的含义描述如下:
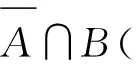
2 拍卖模型构建及投标均衡策略分析
为了解决上述提及的问题,下面分别给出投标者后悔心理行为刻画、拍卖模型构建以及投标均衡策略分析的描述。
2.1 投标者后悔心理行为刻画
在竞拍投标前,投标者不仅会考虑当其投标成功时的预期收益,通常还会考虑当其预期投标失败时的后悔效用,即当投标者预期拍卖最终获胜价不高于自身估价时,其会产生后悔感知。也就是说,投标者在投标前会对可能产生的后悔有所预期,且总是期望其后悔程度尽可能的小,并试图选择使自身期望收益最大同时后悔感知程度最小的投标策略。依据文献[10]和[15],投标者的后悔函数可被表示为
R(Δv)=βΔv,Δv=v-z
(1)
其中Δv表示投标者对拍卖物品的估价v与赢得该物品的获胜价z之间的差值,且Δv≥0;β表示投标者针对未赢得该物品的后悔感知程度,0≤β≤1,且β越大,表示投标者预期的后悔感知程度越大。
进一步地,依据式(1),可计算得到投标者的后悔期望值即后悔感知效用E(R),即
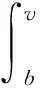
(2)
其中b表示投标者对拍卖物品的投标价,且b∈[0,v];1-L(b)表示投标者投标失败的概率。
2.2 拍卖模型构建
为了构建考虑投标者后悔心理行为的组合拍卖模型,根据文献[4]和[15]分别针对组合拍卖问题和考虑投标者后悔心理行为的拍卖问题的阐述,这里给出如下前提假设:
假设1拍卖者要通过同时拍卖的方式出售两个异质互补性物品(A和B),拍卖规则是第一价格密封式拍卖;
假设2在拍卖中,对一种物品(A或B)感兴趣的局部投标者人数相同且均为定值n,即nA=nB=n,且只存在1个全局投标者r,这些信息对于每个投标者来说都是公共知识;
假设3在拍卖过程中,全局投标者r存在预期后悔心理行为,且投标者r的预期后悔心理行为对其事前期望效用的影响与后悔值的大小成反比,即在投标者期望收益一定时,后悔值越大,则投标者的事前期望效用越小,反之亦然。
这里需要指出的是,在一般组合拍卖甚至是具有某种特殊结构的组合拍卖中,投标策略均很难求得[19],因此,假设1和2是本文模型考虑的一个简单情况;实验研究表明[10~16],投标者在进行投标决策时存在后悔心理行为,并且该心理行为对投标者的期望效用是有影响的,依据实际投标情况可知,假设3意味着投标者的期望效用与自身的后悔心理行为有关。
本文的组合拍卖模型是针对全局投标者构建的事前期望效用计算模型。全局投标者在做出投标决策时,不仅要考虑预期投标成功时的期望收益,同时还要考虑预期投标失败时的后悔感知效用。
当全局投标者r预期投标成功时,其期望收益函数可被表示为

=L(bA)L(bB)(vc-bc)+
[1-L(bA)]L(bB)(vB-bB)+
L(bA)[1-L(bB)](vA-bA)
=L(bA)L(bB)(vA+vB+α-bA-bB)+
[1-L(bA)]L(bB)(vB-bB)+
L(bA)[1-L(bB)](vA-bA)
(3)
当全局投标者r预期投标失败时,其后悔感知效用函数由三部分组成:
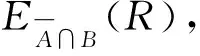

dL(zA|zA≥bA)[1-L(bA)]
(4)
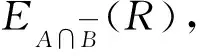
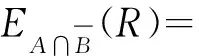
dL(zB|zA≥bB)[1-L(bB)]
(5)

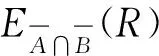
dL(zA|zA≥bA)[1-L(bA)]+
dL(zB|zB≥bB)[1-L(bB)]
(6)
依据式(4)~(6),可得到全局投标者r的后悔感知效用函数E(R)为
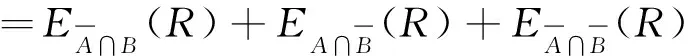
dL(zA|zA≥bA)[1-L(bA)]+
dL(zB|zB≥bB)[1-L(bB)]
(7)
由上述投标者预期投标成功和失败的两种情况分析,关于全局投标者r的组合拍卖模型,即投标者r的事前期望效用可由下式表示:
EUc=π-E(R)
=L(bA)L(bB)(vA+vB+α-bA-bB)+
[1-L(bA)]L(bB)(vB-bB)+
L(bA)[1-L(bB)](vA-bA)-
dL(zA|zA≥bA)[1-L(bA)]-
dL(zB|zB≥bB)[1-L(bB)]
(8)
2.3 投标均衡策略分析
由于组合拍卖中投标策略分析和求解的复杂性[19],特别是将投标者心理行为引入组合拍卖模型,使得投标均衡策略求解变得更加复杂。因此,为了分析的需要,这里有必要对一些变量做如下的假设和转换。

(2)假设局部投标者对每一个拍卖物品的估价相互独立且服从[0,1]范围内的均匀分布[4,15],即F(vij)=vij;
(3)局部投标者的投标价与其估价之间存在增函数关系[20~23],为了便于分析,这里假设两者之间呈线性正比关系,即bij=ρvij,0≤ρ≤1,0≤vij≤1,i=1,2,…,n,j=A,B,显然,bij∈[0,ρ]。
依据假设条件(2)和(3),分布函数L(x)可以转换为
L(x)=P(zj≤x)=P(ρvij≤x)n
=P(vij≤x/ρ)n=(x/ρ)n
(9)
显然,密度函数l(x)为
l(x)=L′(x)=(n/ρ)(x/ρ)n-1
(10)
将式(9)和(10)代入式(8),并化简可得
EUc=α(δbc/ρ)n[(1-δ)bc/ρ]n+
(vA-δbc)(δbc/ρ)n+
[vB-(1-δ)bc][(1-δ)bc/ρ]n-
(11)
针对式(11)求关于bc的一阶导数,即

nδnvA+n(1-δ)nvB+nδnβA(vA+θα-δbc)+n(1-δ)nβB[vB+(1-θ)α-(1-δ)bc]}
(12)
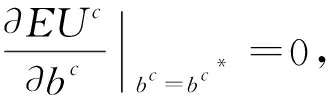
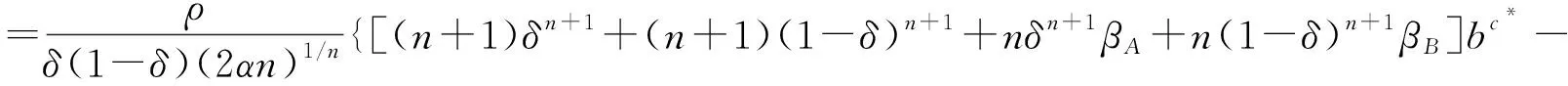
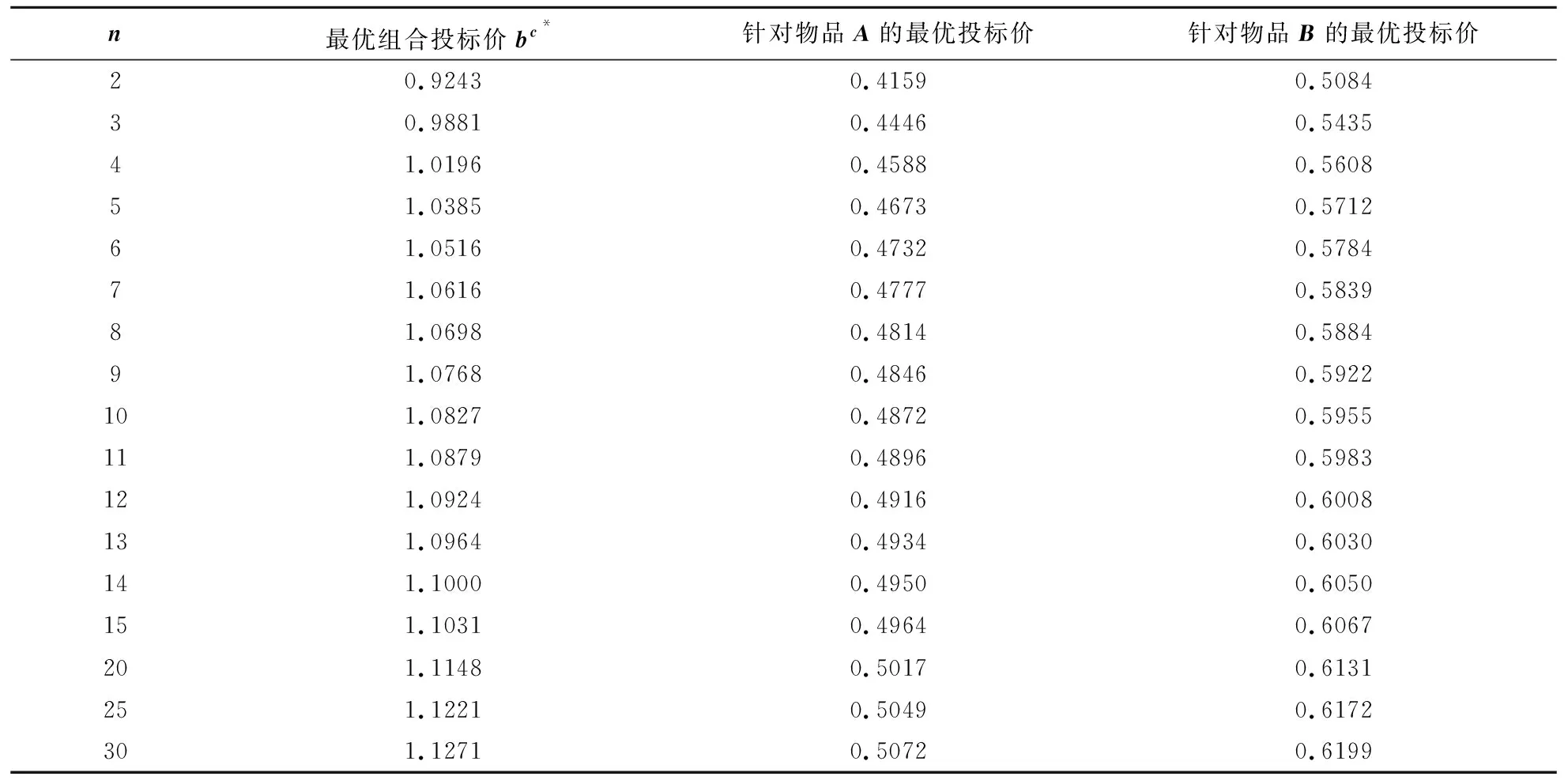
nδnvA-n(1-δ)nvB-nδnβA(vA+θα)-n(1-δ)nβB[vB+(1-θ)α]}1/n,0 (13) 式(13)仅是投标均衡策略bc*满足的必要条件,下面给出其需要满足的充分条件。 针对式(11)求关于bc的二阶导数,即 (n-1)δn[(1+βA)vA+αβAθ]+(n-1)(1-δ)n[(1+βB)vB+αβB(1-θ)]} (14) 本节针对存在若干个局部投标者和一个全局投标者的两个异质物品组合拍卖,在考虑全局投标者后悔心理行为的情形下,通过数值实验分析针对每个物品投标的局部投标者人数、拍卖物品的组合效应及全局投标者后悔参数对全局投标者投标均衡策略的影响。 由数值仿真结果可以观察到:随着对每个物品投标的局部投标者人数增加,全局投标者的最优组合投标价bc*及针对物品A和B的最优投标价均增大,且当n取值较小时(n≤10),bc*的增幅较明显,随着n的继续增加,bc*增幅放缓。这说明,在组合拍卖中,潜在的局部投标者人数越多,拍卖的竞争越激烈,全局投标者若想同时赢得物品A和B,就需要不断提高投标价来增大投标获胜的概率;同时,当潜在的局部投标者人数相对较多时,全局投标者的最优投标价虽然还会增大,但其增幅将明显减小,这是由于此时全局投标者的投标价水平已经很高,虽然在此基础上大幅提高投标价将增大赢得拍卖物品的概率,但是有可能给全局投标者带来负的期望效用,因此,全局投标者会减小bc*的增幅,这与拍卖实际情况相符。 表1 针对每个物品投标的局部投标者人数n对全局投标者的投标均衡策略的影响 当n=2,10和30时,分别代表局部投标者人数少、适中、多三种情况,在4.1节参数α设置的前提下,将组合效应系数视为变量,令依次取0.1,0.15,0.2,0.25,0.3,0.35,0.4和0.45,利用MATLAB7.8.0(R2009a)软件进行数值仿真,可以得到全局投标者的投标均衡策略随α的变化规律,如表2~4所示。 由数值仿真结果可以观察到:随着组合效应系数值增加,全局投标者的最优组合投标价bc*及针对物品A和B的最优投标价均增大,即拍卖物品的组合给全局投标者带来的组合效应越大,全局投标者的投标价就越高,且随着局部投标者人数增多,全局投标者在各个组合效应水平的最优投标价都将增大。这说明,在组合拍卖中,若全局投标者认为获得的组合效应越大,那么同时赢得所有拍卖物品对其越有利,相应地,最优投标价就越高;同时,当参与拍卖的局部投标者人数增多时,拍卖竞争加剧,全局投标者需要支付更高的投标价来赢得拍卖物品的组合。 表2 组合效应系数α对全局投标者的投标均衡策略的影响(n=2) 表3 组合效应系数α对全局投标者的投标均衡策略的影响(n=10) 表4 组合效应系数α对全局投标者的投标均衡策略的影响(n=30) 当n=2,10和30时,分别代表局部投标者人数少、适中和多三种情况,在3.1节参数设置的前提下,将全局投标者针对每个拍卖物品的后悔参数(βA,βB)视为变量,令(βA,βB)依次取(0.1,0.15),(0.15,0.2),(0.2,0.25),(0.25,0.3),(0.3,0.35),(0.35,0.4),(0.4,0.45),(0.45,0.5),(0.5,0.55),(0.55,0.6)和(0.6,0.65),利用MATLAB 7.8.0(R2009a)软件进行数值仿真,可以得到全局投标者的投标均衡策略随(βA,βB)的变化规律,如表5~7所示。由数值仿真结果可以观察到: 1)在任一局部投标者人数状态下(n),全局投标者最优组合投标价bc*及针对物品A和B的最优投标价均与全局投标者的后悔参数值(后悔感知程度)呈正相关关系。这是由于全局投标者的后悔感知程度越高,其错失一个以合适的价格赢得组合拍卖的机会的概率就越大,因此,全局投标者需要不断提高自身投标价来削弱其预期后悔感知,同时增大拍卖获胜概率。 2)针对同一后悔参数组合(βA,βB),全局投标者最优投标价bc*与局部投标者人数n呈正相关关系。这是因为,在一定的预期后悔感知情况下,若全局投标者得到的局部投标者人数信号越强,即局部投标者人数越多,则竞拍的激烈程度就越强,伴随着拍卖竞争加剧,全局投标者需要支付更高的投标价来赢得拍卖物品组合。 表5 全局投标者后悔参数(βA,βB)对其投标均衡策略的影响(n=2) 表6 全局投标者后悔参数(βA,βB)对其投标均衡策略的影响(n=10) 表7 全局投标者后悔参数(βA,βB)对其投标均衡策略的影响(n=30) 为了进一步说明上文给出的组合拍卖模型及全局投标者投标均衡策略分析方法的潜在应用,这里给出无线电频谱组合拍卖的全局投标者投标均衡策略确定的一个算例分析;基于算例的参数取值,进一步给出本文所提方法与相关投标策略确定方法的比较分析。 无线电频谱作为一种稀缺不可再生的资源,在各国政治、军事和经济领域均占有重要的战略地位。如何合理高效地分配和管理频谱资源是一项艰巨而紧迫的工作[5]。针对无线电频谱这种特殊的公共资源,一些学者指出采用拍卖的模式来分配会更有效[28,29]。这里,考虑中国S地区的无线电管理部门欲采用一级价格组合拍卖的方式,将本地区内两个相邻区域的3.5GHz频段上两段带宽无线接入频谱1×150MHz(频谱A)和1×200MHz(频谱B)分配给市场上的电信运营商。经过初步资格审查后,共有9个合格的运营商允许参加拍卖,其中只对单一频谱A或B感兴趣的局部投标者个数均为4,即n=4,而对两个频谱均感兴趣的全局投标者个数为1(记该全局投标者为r)。这种情形可以理解为,无线电管理部门同时同地开设两个拍卖各拍卖一个频谱,有8个运营商(局部投标者)分别参加自己感兴趣的某个拍卖,运营商r(全局投标者)则会同时参加两个拍卖。假设局部投标者对频谱A或B的估价服从[0,1]上的均匀分布,且局部投标者的投标价范围为[0,ρ]=[0,0.8](单位:百万元);全局投标者r对于频谱A和B的估价分别为60万元和70万元,即vA=0.6,vB=0.7,且其认为两个频谱A和B的组合能带来互补性效用α=0.2,频谱A对组合效应的贡献度θ=0.5,全局投标者r的后悔参数为βA=0.4,βB=0.45。根据本文给出的全局投标者投标均衡策略分析过程,来确定其在该组合拍卖中的投标均衡策略。 特别地,当后悔参数βA=βB=0时,即不考虑全局投标者后悔心理行为的情形,组合拍卖模型退化为 EUc=π=L(bA)L(bB)(vA+vB+α-bA-bB)+[1-L(bA)]L(bB)(vB-vB)+L(bA)[1-L(bB)](vA-bA) =α(δbc/ρ)n[(1-δ)bc/ρ]n+(cA-δbc)(δbc/ρ)n+[vB-(1-δ)bc][(1-δ)bc/ρ]n 通过与考虑全局投标者后悔心理行为的情形对比,可以发现,在不考虑全局投标者后悔心理行为的情形下,全局投标者的期望效用仅由其预期投标获胜的期望收益决定,由此求得的最优投标价相对较低。而在实际拍卖中,全局投标者通常会存在针对投标失败的预期后悔感知,为了使得自身后悔程度尽可能小同时获胜收益尽可能大,其往往会提高自身投标价水平,这也进一步解释了实际拍卖中常出现的超投标的现象。 基于4.1节参数的具体取值,即n=4,ρ=0.8,α=0.2,vA=0.6,vB=0.7,βA=0.4,βB=0.45,且假设局部投标者的投标者价值服从[0,1]范围内的均匀分布,针对由本文得到的投标均衡策略(包括考虑全局投标者后悔心理行为与不考虑后悔心理行为两种情形)与未考虑投标者心理行为的组合拍卖投标均衡策略[4]和考虑投标者后悔心理行为的单物品拍卖投标均衡策略进行比较分析[15,16],比较结果如表8所示。由表8可以看出,由Krishna和Rosenthal[4]确定的未考虑投标者心理行为的组合拍卖投标策略与本文得到的不考虑全局投标者后悔心理行为情形下的投标策略大致相等,即1.1058≈1.1162,同时,其小于本文在考虑全局投标者后悔心理行为情形下得到的投标策略,即1.1058<1.2449,这主要是由于Krishna和Rosenthal没有考虑全局投标者在拍卖过程中的预期后悔心理行为(可视为预期后悔感知程度为0的特殊情形),而3.3节数值实验分析结果表明,全局投标者的预期后悔感知程度与其投标策略呈正相关关系,因此,在一定条件下(βA=βB=0),由Krishna和Rosenthal确定的投标策略仅是本文得到结果的一个特例,其无法解释组合拍卖中的超投标经济现象;Engelbrecht-Wiggans和Katok[15]、高广鑫和樊治平[16]确定的均是在考虑投标者后悔心理行为情形下的单物品拍卖投标策略,为了便于比较分析,我们计算了文献[15]和[16]分别针对物品和的最优投标价,在此基础上,将计算得到的两个单物品投标价合成组合投标价,由表8可知,由文献[15]和[16]确定的投标策略大致相等,即1.1062≈1.107,但二者均明显小于本文在考虑全局投标者后悔心理行为情形下得到的投标均衡策略,即1.1062≈1.107<1.2449,甚至其小于本文在不考虑全局投标者后悔心理行为情形下得到的投标均衡策略,即1.1062≈1.107<1.1162,这主要是由于文献[15]和[16]是针对单物品拍卖确定的投标策略,其没有考虑组合拍卖中多物品之间的组合给全局投标者带来的组合效应,而3.2节数值实验分析结果表明,拍卖物品给全局投标者带来的组合效应与其投标策略呈正相关关系,因此,由文献[15]和[16]确定的投标策略不能适用于多物品组合拍卖的环境。综上,由本文确定的考虑全局投标者后悔心理行为的投标均衡策略,不仅能够反映全局投标者在组合拍卖过程中表现的后悔规避心理行为,而且符合多物品组合拍卖的实际情况和特点。 表8 本文所提方法的结果与相关方法所得结果的比较 本文研究了考虑全局投标者后悔心理行为的组合拍卖的全局投标者投标均衡策略确定问题,在采用Engelbrecht-Wiggans和Katok提出的后悔函数刻画投标者后悔心理行为的基础上,构建了组合拍卖模型,通过分析得出了全局投标者投标均衡策略需要满足的充分和必要条件,同时依据构建的模型对影响全局投标者投标均衡策略的三个重要参数(局部投标者人数、组合效应系数和全局投标者后悔参数)进行了数值仿真,进一步地,通过一个关于无线电频谱组合拍卖的算例说明了本文构建的模型及投标均衡策略分析方法的潜在应用。与已有相关研究不同的是,本文着重考虑了组合拍卖中全局投标者存在后悔心理行为的情形,并分析了这类投标者的投标均衡策略。通过本文的研究,得到以下主要结论: 1)在组合拍卖中,全局投标者的后悔心理行为对于其投标均衡策略具有重要的影响,与不考虑全局投标者后悔心理行为的情形相比较,存在预期后悔感知的全局投标者会提高其投标价,这一结论有利于解释实际组合拍卖中的超投标现象; 2)在考虑全局投标者后悔心理行为的组合拍卖中,其最优投标价通常随局部投标者人数、组合效应系数和全局投标者后悔参数的增加而增加。 本文构建的组合拍卖模型和全局投标者投标均衡策略分析方法,为解决现实中考虑全局投标者心理行为的组合拍卖投标策略确定问题,提供了一种新的途径。与其他相关的投标均衡策略确定方法相比,运用本文方法确定的投标均衡策略,较好地反映了全局投标者的预期后悔心理行为,符合多物品组合拍卖投标的现实情况。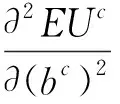
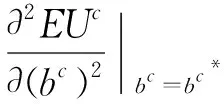
3 数值实验
3.1 局部投标者人数对全局投标者的投标均衡策略的影响

3.2 组合效应系数对全局投标者的投标均衡策略的影响

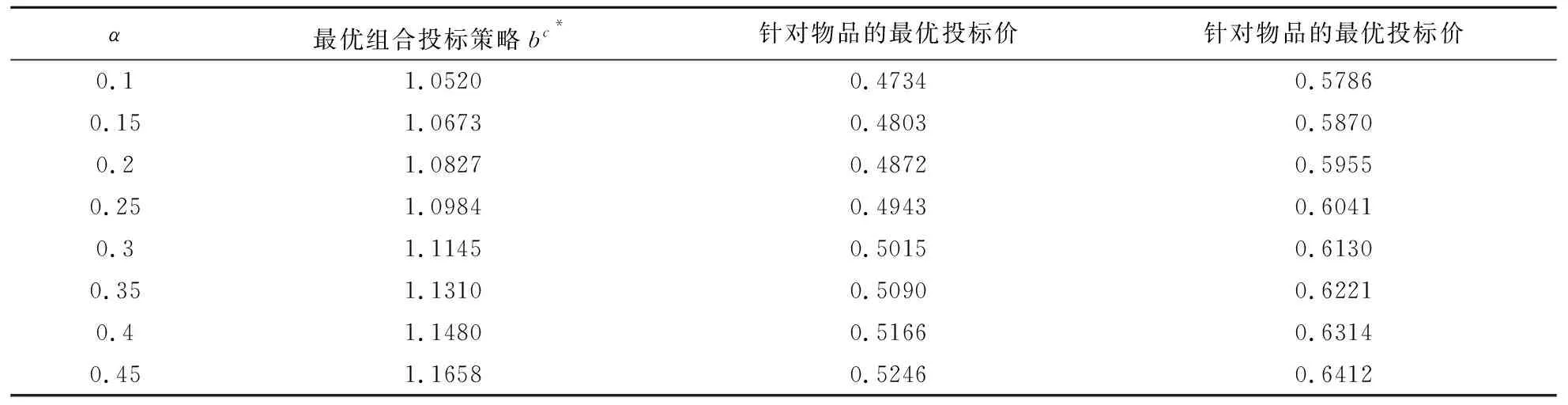

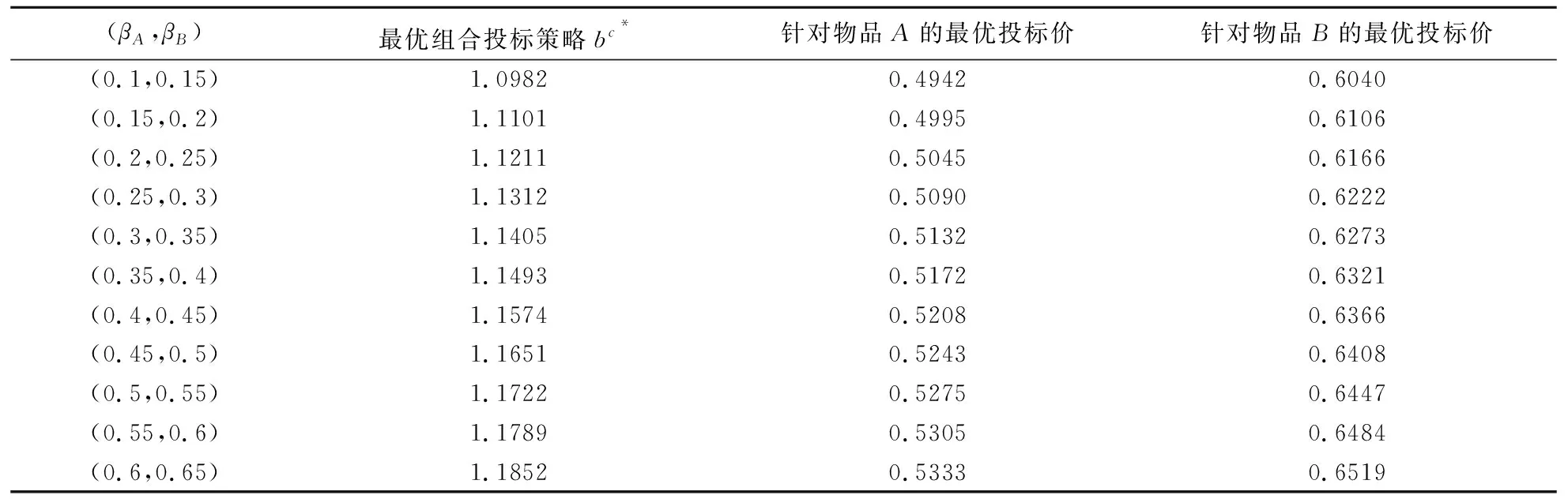
3.3 全局投标者后悔参数对其投标均衡策略的影响


4 算例分析
4.1 无线电频谱组合拍卖的投标均衡策略
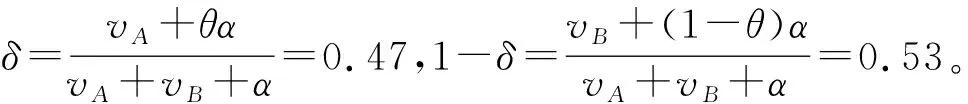


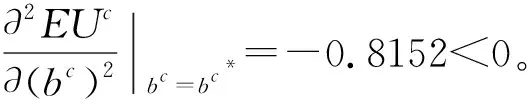
4.2 投标均衡策略确定方法比较分析

5 结论

