考虑不同商业目标和公平关切的动态博弈模型及复杂性研究

李秋香， 张玉豪， 黄毅敏， 齐二石

(1.河南大学 管理科学与工程研究所，河南 开封 475004； 2.河南大学 商学院，河南 开封 475004； 3.华北水利水电大学 管理与经济学院，河南 郑州 450046； 4.天津大学 经济与管理学部,天津 300072)

0 引言

近些年，随着电子商务和信息技术的迅速发展，网上直销渠道的兴起对消费者的消费方式产生了巨大的影响，网上购物越发受到消费者的青睐。数据显示，2016年我国零售百强企业实现销售额4.82万亿元，同比增长18.5%；《2016年中国零售百强榜名单》中仅有6家电商上榜，但其销售额占零售百强总销售额的51.2%。在电子商务的背景下，市场趋于多元化，市场竞争激烈，零售商的商业行为在企业决策中具有举足轻重的作用，研究零售商的商业行为对市场竞争的影响尤为重要，如设定不同的商业目标，考虑公平关切, 风险规避等行为具有一定的理论和现实意义。

众多学者对市场决策者的商业目标和公平关切行为做了广泛深入的研究。先前的研究大多认为企业最大的经营目标是利润最大化，但现实中企业的经营目标不仅关注利润获得，而且还关注销售收入，市场份额甚至顾客满意行为[1,2]，尤其在寡头市场竞争中，抢占市场份额成为寡头竞争的重要决策部分。Cooper等[3]和Carpenter等[4]阐述了利润与市场份额的关系，前者指出商业经营者需要关注市场份额指标，其能度量产品的绩效或品牌的市场地位，后者认为一种品牌的市场行为能够影响竞争者的市场份额。David等[5]在对众多研究基础上，分析得出在通常情况下，市场份额对商业盈利有积极的影响。Biplab等[6]比较全面的研究了市场份额，利润和其它商业目标的关系，通过建立数学市场模型的元博弈分析，预测了市场份额，利润及其它商业因素的一系列情景。以上文献研究了市场份额，利润等之间的相互关联，但没有考虑市场份额，不同商业目标等对系统稳定性及利润获得的具体影响。Li等[7]分析了寡头零售商考虑不同商业目标的情况并对建立的模型进行了复杂性分析，研究发现企业考虑市场份额会扩大系统的稳定域，但没有考虑决策者的公平关切行为。

近些年，许多学者将市场参与者的心理行为引入供应链中加以研究，行为供应链的相关研究发展迅速。在市场竞争中，决策者通常会关注公平问题，表现出公平关切行为，在公平关切的行为下，竞争者有可能会感到不公平时以己方利益受损为代价采取行动达到惩罚对方的目的[8]。Cui等[9]认为当供应链成员考虑公平关切时，制造商倾向于制定简单的转移价格契约使供应链协调，并介绍和分析了制造商和零售商之间考虑相对利润的公平关切模型。Pavlov和Katok等分别研究了公平关切行为对供应链协调以及公平关切作为私人信息情况下对批发价格决策的影响[10,11]。杜少甫等[12]研究了零售商具有公平关切对供应链协调性的影响且给出了零售商考虑绝对利润的公平关切模型。更多学者将公平关切行为引入到不同供应链领域或加入其它因素综合研究。孙玉玲等[13]分析了收益共享契约下, 供应链成员具有公平关切的鲜活农产品供应链协调问题。刘琦铀等[14]考虑了公平关切下的鲜活农产品供应链收益共享契约问题。周艳菊等[15]分析了零售商考虑公平关切对低碳供应链最优决策及渠道协调的影响。石松等[16]研究了低碳供应链中制造商公平关切行为对供应链定价策略及利润的影响。Li等[17]在考虑公平关切行为情景下，分析了零售商增加产品服务行为的最优价格策略。刑伟等[18]分析了双渠道供应链中公平关切对合作伙伴决策的影响。Choi等[19]和Katok等[20]分别通过一个实验性研究分析了公平关切在竞争性供应链关系的作用和供应链合同中的公平问题。Hornibrook等[21]探究了供应链中公平关切与组织产出的关联。Feng等[22]分析了基于私人成本信息的公平关切下的供应链异常表现。Li等[23]研究了双渠道供应链中考虑公平关切的制造商的广告合作问题。Qu等[24]研究了二阶双渠道供应链中制造商考虑公平关切的价格最优问题。许明辉等[25]和姚锋敏等[26]分别分析了公平关切对零售商期权合约的协调作用以及零售商主导的闭环供应链成员决策最优化问题。

以上文献将公平关切行为引入到供应链领域，对考虑不同因素影响下的供应链进行了广泛而深入的探讨，主要体现在供应链价格决策和渠道协调等方面的研究。但很少学者对供应链成员同时考虑不同商业目标和公平关切的情景进行建模并进行动态复杂性研究。

本文将研究由两个零售商组成的寡头市场，构建双寡头动态价格博弈模型并对其均衡点的复杂演化特征进行分析。关于寡头竞争及复杂性分析的研究一直受到学者关注。Rand指出在Cournot模型调整过程中，可能出现Nash均衡消失继而出现混沌现象[27]。Puu发现双寡头Cournot模型中会出现混沌吸引子并讨论了三寡头博弈竞争的情景[28]。众多学者研究了不同情景下的供应链价格博弈模型的复杂特质。Huang等[29]考虑企业社会责任，研究了风险规避型寡头市场的价格演化复杂特征。Huang等[30]建立了基于非线性需求方程的Cournot-Bertrand混合模型，分析了互补品市场价格竞争的动态复杂性质。以上文献将数学分析和数值仿真结合来分析对应的模型，为复杂系统的动态博弈研究提供了很好的方法。

本文考虑零售商具有不同商业目标和公平关切行为，首先构建寡头动态博弈模型，运用博弈论和非线性动力学理论分析系统的均衡点及稳定性，然后用数值仿真方法对系统的动态演化过程进行分析；最后建立系统的控制模型，对市场的混沌行为进行控制。研究结论对具有不同商业目标和公平关切行为的零售商在价格博弈方面具有一定的指导作用。

1 问题描述和效用方程的构建

1.1 问题描述与模型假设

本文考虑了两个零售商(零售商1和零售商2)销售两种具有相互替代作用的商品，零售商1拥有传统线下销售渠道和网上直销渠道，零售商2仅有网上直销渠道。两个零售商在同一市场进行价格竞争但在一个博弈周期内任何一方都不知道对方的竞争价格策略。由于在一个博弈周期内，市场参与者受市场复杂因素的影响以及不能得到市场决策的全部所需信息(如决策者的认知能力，收集处理信息的能力，经济及环境因素)，故假设零售商具有有限理性和不完全信息。零售商1具有双重商业目标—利润获得和市场份额，零售商2以利润最大化为经营目标且具有公平关切行为。

图1 供应链系统

其中TS,DS分别表示传统线下销售渠道和网上直销渠道，p1,p2分别是零售商1传统线下销售渠道和网上直销渠道的价格，p3是零售商2网上直销渠道销售价格。

1.2 效用方程的构建

文中变量和参数表示符号和含义如下：

Di(t):零售商i(i=1,2, 3)第t期零售商的需求函数;a:销售渠道的潜在的市场规模;θ:消费者对传统线下销售渠道的忠诚度;θa:传统线下销售渠道潜在的市场规模;(1-θ)a:网上直销渠道潜在的市场规模;b:零售商i(i=1,2)的价格弹性系数;k:零售商i(i=1,2)的交叉价格弹性系数;c:零售商i(i=1,2)销售商品的单位成本;v:零售商1的商业目标平衡系数;λ:零售商2的公平关切系数。

根据文献[7,10]，假设零售商1和零售商2第t期的线性需求函数如下：

D1(t)=θa-bp1(t)+kp2(t)+kp3(t)

D2(t)=(1-θ)a-bp2(t)+kp1(t)+kp3(t)

(1)

D3(t)=(1-θ)a-bp3(t)+kp1(t)+kp2(t)

其中b>k>0，a足够大满足市场需求。

零售商1和零售商2第t期的利润函数：

(2)

其中零售商1的利润等于传统销售渠道利润πt和网上直销渠道利润πd之和，πt=(p1(t)-c)D1(t),πd=(p2(t)-c)D2(t)。

Du等[12]研究了零售商的公平关切行为，给出了零售商的效用方程如下:ur=πr-β(πm-πr),其中πm,πr分别表示制造商和零售商的利润，零售商的公平关切感知取决于与制造商绝对利润的比较，即零售商将制造商的利润作为利润参考依赖点。当零售商的利润低于制造商的利润时，零售商的效用会减小，零售商的利润大于制造商的利润时，零售商的效用会增加。

Cui等[9]也给出了零售商考虑公平关切的效用方程：

u(w,p)=π(w,p)+fr(w,p)

fr(w,p)=-αmax(γΠ(w,p)-π(w,p),0)

-βmax(π(w,p)-γΠ(w,p),0)

其中Π(w,p)，π(w,p)分别表示制造商和零售商的货币报酬，γΠ(w,p)是零售商选择制造商的γ部分利润作为其利润参考指标，α,β分别为零售商感知到不平等时，自身愤怒和怜悯情景下效用损失的敏感系数；公平感知取决于零售商利润与制造商的部分利润的比较，只要γΠ(w,p),π(w,p)两者之间不相等都会使得零售商的效用小于其利润。

本文参考文献[12]中的零售商公平关切效用模型，得出零售商1和零售商2的效用函数方程：

(3)

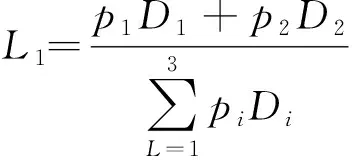
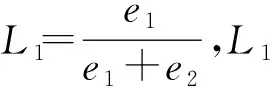
可知，零售商1的销售额与其市场份额成正方向变化，即两者变化趋势相同，因此可用零售商1的销售额e1=p1D1+p2D2表示其所占的市场份额[7]。

2 离散动态博弈模型及其复杂性分析

本节建立双寡头零售商的离散动态模型，求解并分析均衡点的稳定性，在系统稳定域内，只要零售商的价格调整速度保持在稳定域内，零售商经过有限次的价格博弈后，系统都会稳定在纳什均衡点。

2.1 离散动态博弈模型

根据效用方程(3)，可求零售商1和零售商2的边际效用函数，对效用方程求一阶偏导数可得：

(4)

基于双方有限理性和市场信息不完全情况下，博弈双方将本期的边际效用函数作为下期的价格变动参考依据，即当期的边际效用大于零，下个博弈周期零售商会提高价格；当期边际效用小于零，下个博弈周期零售商会降低价格；由此建立动态博弈方程，表示如下：

(5)

其中α1,α2,α3分别表示零售商1和零售商2的价格调整系数且α1,α2,α3>0。

2.2 系统平衡点

令系统(5)中pi(t+1)=pi(t)，可以得到系统(5)的平衡点,Ej=(p1,p2,p3),j=1,2,…,8;系统平衡点表示如下：

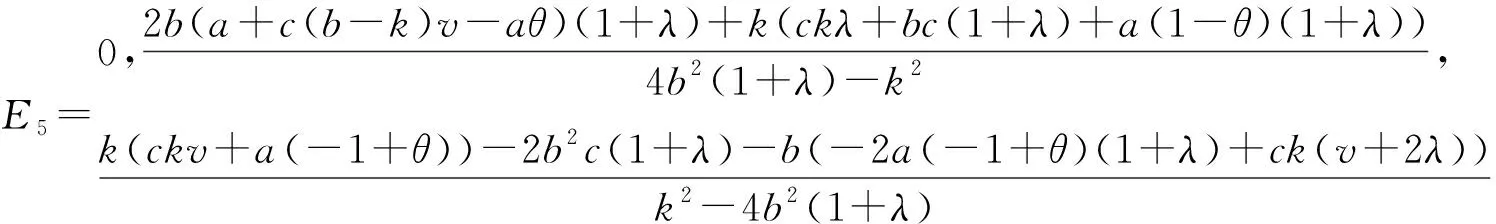
下面对均衡点的稳定性进行分析验证，系统(5)的Jacobi矩阵J(p1,p2,p3)表示如下：

(6)

其中:J11=1+α1(αθ+b(cv-4p1)+k(2p2+p3-cv)),J22=1+α2(a-4bp2+bcv+k(2p1+p3-cv)-αθ),J33=1+α3(b(c-4p3)(1+λ)+a(1-θ)(1+λ)+k(p1+p2+cλ+p1λ))。

将均衡点依次带入Jacobi矩阵，并求得各平衡点相应的特征值，如果特征值非零且大于1，则此均衡点为非稳定点。

以E1为例，得到对应的Jacobi矩阵

求得J(E1)的非0特征值分别为1+α1(aθ+bcv-kcv)，1+α2(a+bcv-k(aθ+cv),1+α3(bc(1+λ)+a(1-θ)(1+λ)+kcλ)，根据上述对各参数的范围定义可得以上特征值均大于1，故E1为不稳定均衡点，同理可得E2,…,E7均为不稳定均衡点，E8是系统(5)唯一的Nash均衡点，其稳定性需要满足Routh-Hurwitz稳定判据，Jacobi的特征多项式表示如下：

F(ξ)=A0+A1ξ+A2ξ2+ξ3

(7)

系统稳定需要满足的条件如下:

其中A0=J11J23J32+J12J21J33+J13J22J31-J11J22J33-J13J21J32-J12J23J31,A1=J11J22+J11J33+J22J33-J13J31-J12J21-J23J32,A2=-J11-J22-J33。

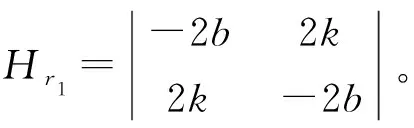
上述已知,b>k>0,-2b<0,4b2-4k2>0,故一阶主子式小于0，二阶主子式大于0，所以海塞矩阵是负定矩阵，即零售商1的效用方程存在唯一最大值。

3 数值模拟

通过数值仿真分析不同参数组合下不同商业目标系数和公平关切水平对系统稳定性及利润的影响。

3.1 稳定域分析

本节采用数值模拟分析系统(5)的稳定性及动态行为。根据市场实际情况，取系统参数如下:a=1,b=0.5,k=0.2,c=0.1,θ=0.6。根据系统稳定性条件，模拟给出零售商1和2的系统稳定域。

(1)商业目标平衡系数对系统稳定性的影响

图2、图3和图4描述了在其它参数不变的情况下，商业目标平衡系数变化对系统稳定域的影响，其稳定域坐标轴由零售商的价格调整速度αi(i=1,2,3)表示，在由αi为坐标轴的稳定域中，只要零售商的价格调整速度取值没有超过稳定域，则零售商经过有限次的价格博弈之后，价格依然会稳定在纳什均衡点。可以看出，α3=0.5和v分别取0,0.5,1时，零售商1的传统销售渠道和网上直销渠道的价格调整速度稳定范围减小，稳定域变小，市场竞争减弱。

结论1双寡头零售商竞争中，零售商拥有传统线下销售渠道和网上直销渠道时，考虑不同的商业目标会使其稳定域减小，系统中市场竞争减弱。

图2 v=0,λ=α3=0.5,时系统(5)三维稳定域和二维稳定域

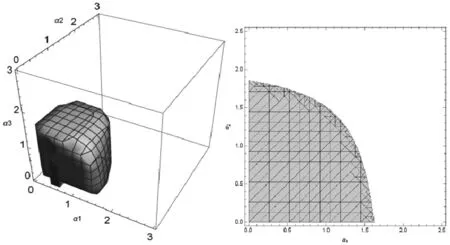
图3 v=0.5,λ=α3=0.5,时系统(5)三维稳定域和二维稳定域

图4 v=1,λ=α3=0.5,时系统(5)三维稳定域和二维稳定域

(2)公平关切水平对系统稳定性的影响

由αi(i=1,2,3)为坐标轴形成的图5、图6和图7依次分析了αi=0.5时，λ=0,0.5,1的情景，三维稳定域随λ的增大而减小；二维稳定域中，α2的范围变化微小，α3的数值范围较大幅度减小。零售商2的公平关切行为对系统的稳定性产生很大影响，公平关切水平越高，对应的稳定域越小。

结论2零售商1和零售商2组成的系统中，零售商2的公平关切行为影响自身的稳定域，且公平关切水平越高，自身稳价格调整的稳定范围变小，系统稳定域变小，市场竞争减弱。

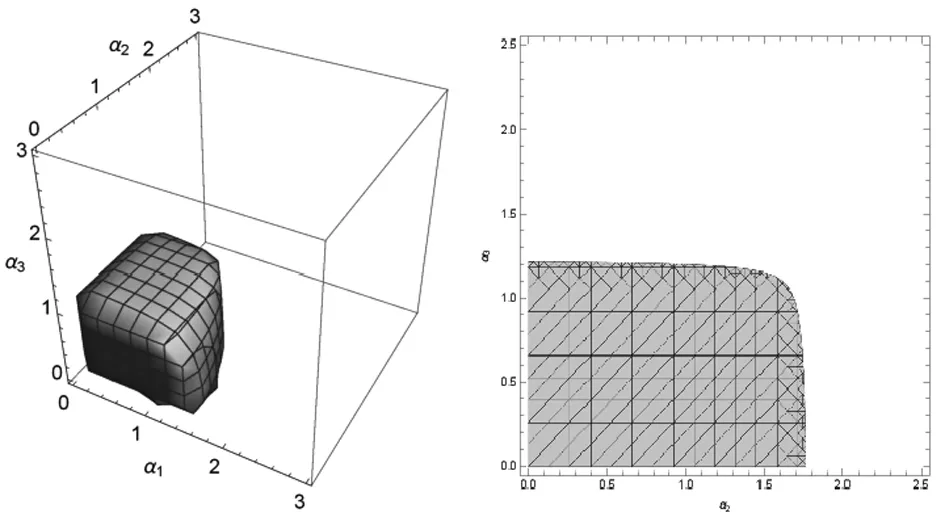
图7 λ=1,α1=0.5,V=0.6时系统(5)三维稳定域和二维稳定域

3.2 价格调整系数对系统价格博弈的影响

通过对系统稳定域的分析可知，当某一零售商的价格调整系数超过稳定域的范围时，系统会失去稳定性甚至出现混沌现象；价格分岔图及李雅普诺夫指数(LLE)是证明系统混沌的重要依据。下面分析零售商1和零售商2的价格调整系数对系统的影响。

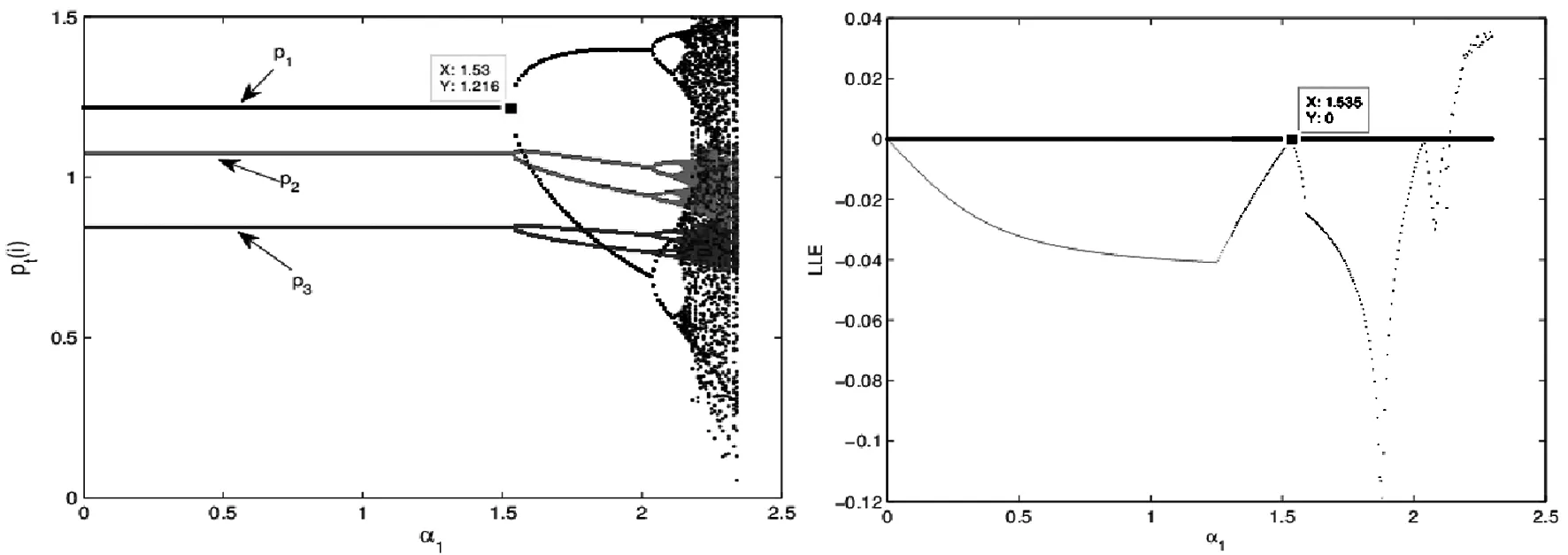
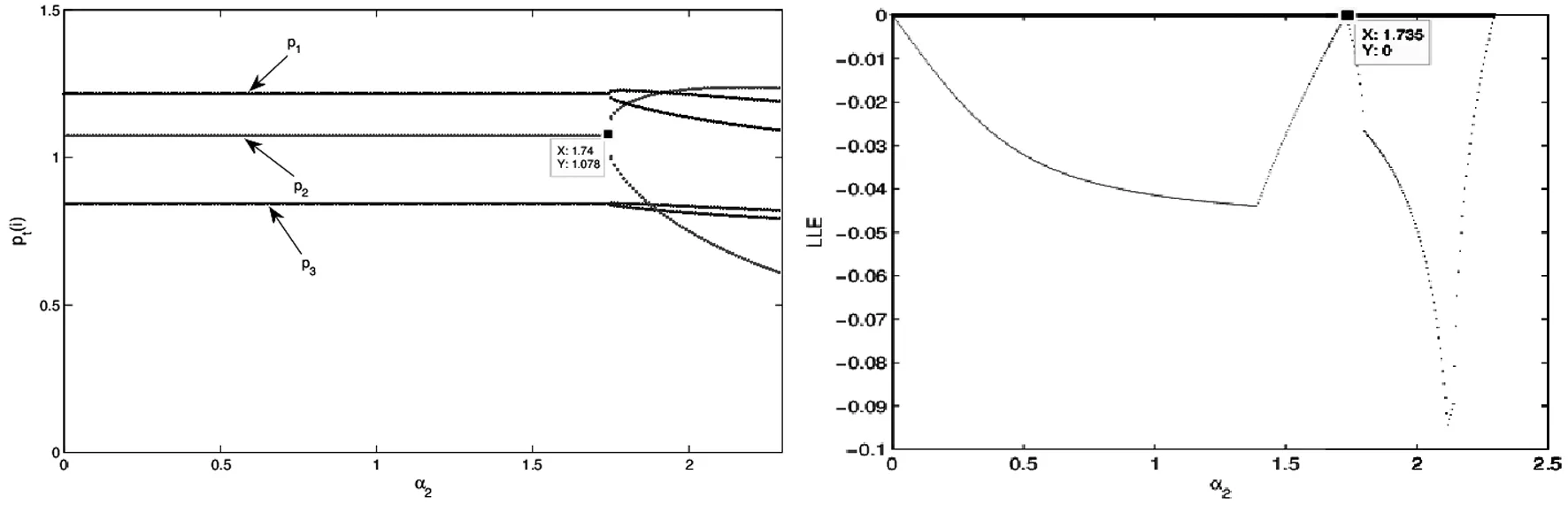
图9 α1=α3=0.5,λ=0.5时系统(5)的价格博弈演化图和李雅普诺夫指数

图8描述了当α2=α3=0.5时，p1,p2,p3随α1变化的价格演化图，当α1<1.53时，系统价格处于稳定状态，当α1=1.53时系统价格出现二周期分岔现象，随着α1的不断增大，系统经历倍周期分岔最后进入混沌状态，此时系统失去稳定且变得不可预测；对应的李雅普诺夫指数验证了价格博弈的演化过程；当LLE小于0时，系统处于稳定状态，当LLE等于0时，系统出现分岔现象，当LLE大于0时，系统处于混沌状态。图9是系统随α2变化的价格博弈过程，当α2=1.74,价格出现二周期分岔现象，随后保持稳定状态，对应的李雅普诺夫指数是负数；当α2>2.3时，零售商1将退出市场竞争。图10为系统随零售商2的价格调整系数α3变化的价格动态过程，当α3=1.55时价格出现二周期分岔现象，经历倍周期分岔最后进入混沌状态。

结论3市场竞争中，零售商的价格调整系数应该控制在一定范围内，当某一零售商的价格调整系数过大时，系统价格会出现分岔现象甚至陷入混沌状态。

3.3 公平关切水平对系统价格博弈的影响

下面研究零售商2的公平关切水平对系统价格演化过程的影响，以α3的变化为例。

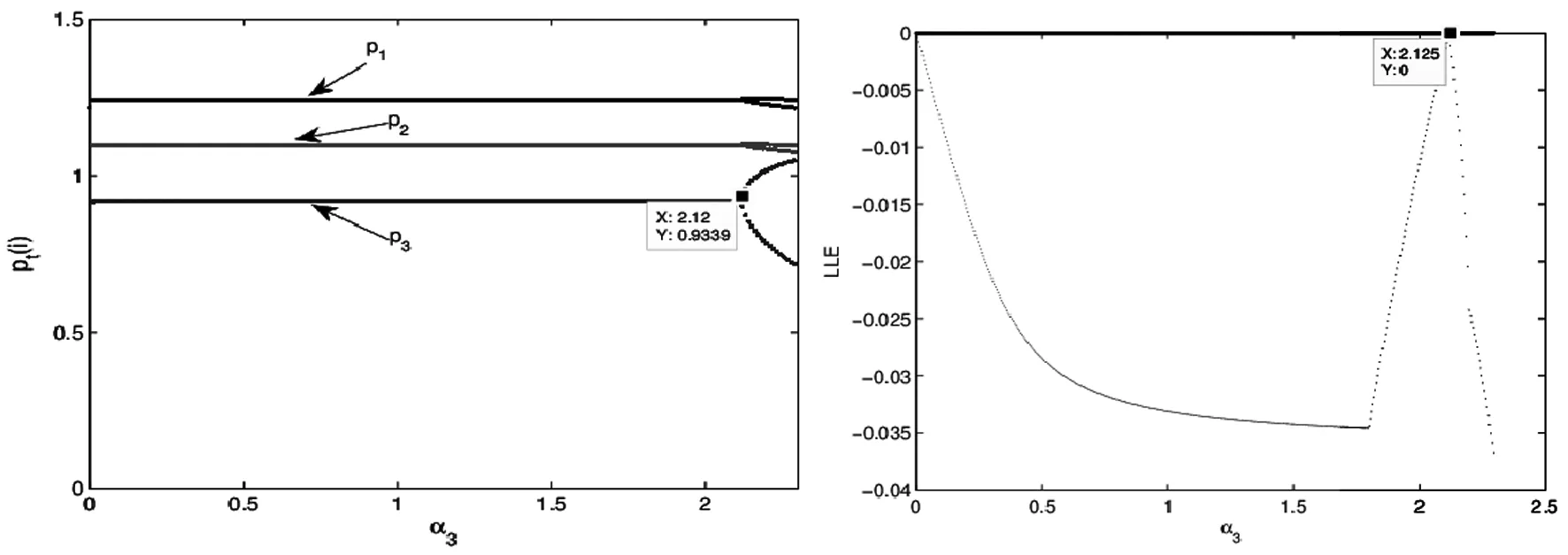
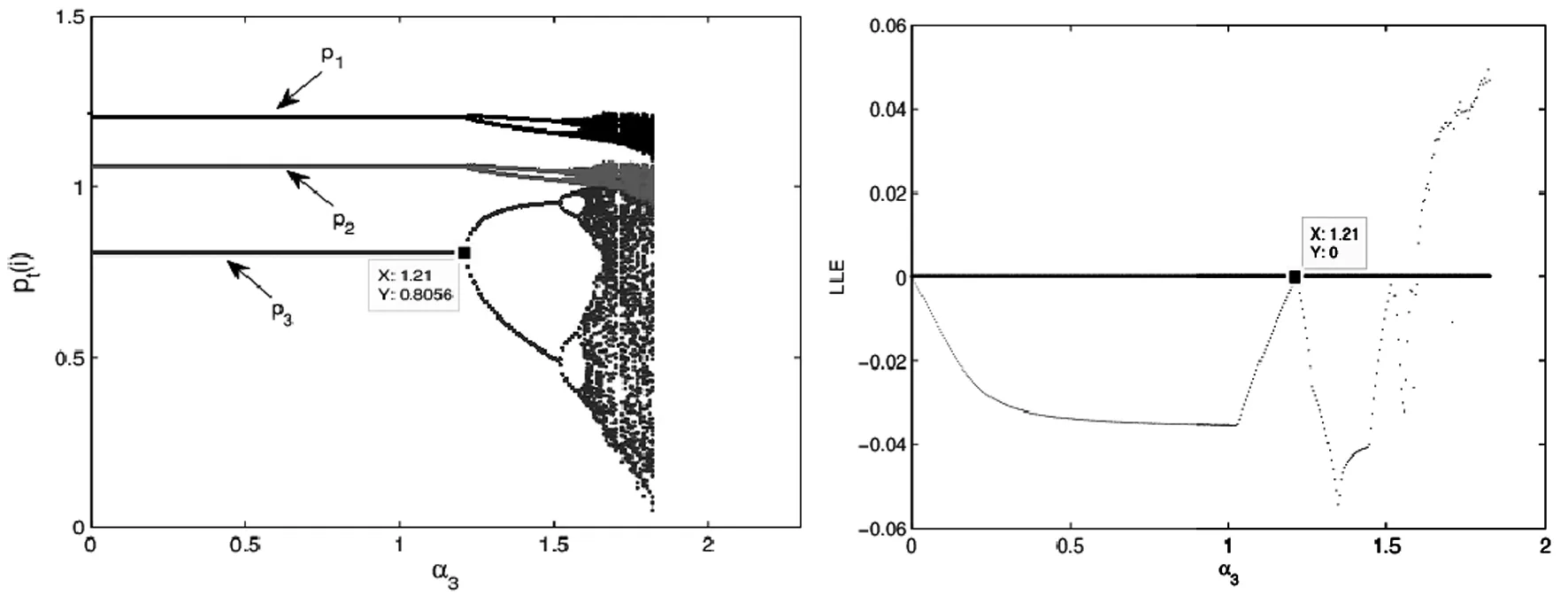
图12 α1=α2=0.5,λ=1时系统(5)的价格动态变化图和李雅普诺夫指数

通过对图10、图11和图12分析可知，当α1=α2=0.5时，系统的稳定性随取值的增大而减小，λ=0时，系统维持在稳定状态，λ=1时，系统很快进入混沌状态且零售商2的价格调整速度范围较大程度的缩小。

结论4考虑公平关切会导致系统较早陷入混沌状态且公平关切的水平越高，系统越容易进入混沌状态。

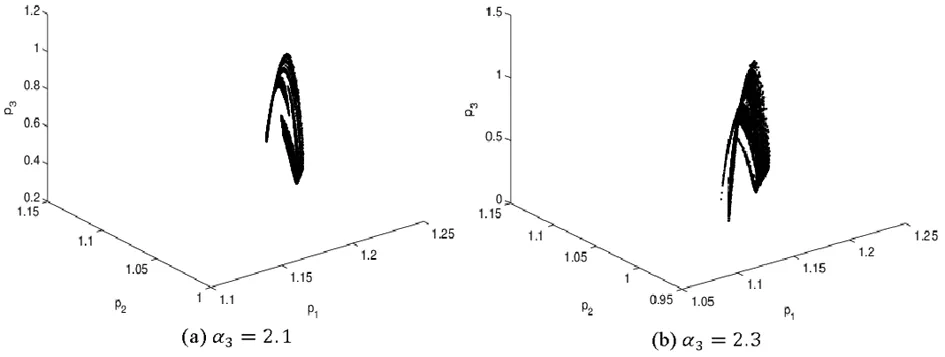
图13 α1=α2=0.5系统(5)的系统混沌吸引子

图14 α1=α2=0.5系统(5)的价格时间序列

图15 α1=0.5,α2=1.0,α3分别为1.6和2.3时系统敏感性且价格初始值为(1.216,1.073,0.843)和(1.216,1.073,0.844)

图13为系统的混沌吸引子，是系统混沌状态的重要特性之一，价格分布在不稳定空间轨道上，验证了价格博弈的动态性。图14表示系统价格的时间序列，当α3=2.0时价格出现四周期分岔，当α3=2.3时，p1,p2,p3的变化处于无序状态，此时系统陷入混沌状态。图15为混沌系统的另一性质—混沌系统对初值的敏感依赖性，系统初始值有微小的变化，就会引起系统价格的剧烈波动，保持p1,p2初始值不变，p3的初始值变化0.001，系统就会发生剧烈变化；当α3=1.6时，p1,p2,p3经历较大波动后逐渐回到初始值，即系统恢复稳定性，当α3=2.3时，p1,p2,p3出现连续无规律的波动，此时系统陷入混沌状态。

3.4 价格调整速度,公平关切水平对零售商利润的影响

利润是评价零售商绩效的重要指标之一。首先以α3变化为例分析价格调整速度对零售商利润影响，随后分析价格调整速度，公平关切水平双因素同时对零售商利润的影响。图16中,当α3=2.3时，系统处于混沌状态，零售商1和零售商2的利润剧烈波动且大部分利润低于稳定时利润值，零售商2的利润甚至出现负值，这不利于零售商利润的最大化。平均利润随α3从0到2.3变化的过程中，系统稳定状态的利润平均值高于系统混沌状态的利润平均值，α3越大，零售商利润损失越大。

图17中(a),(b)分别描述了系统在稳定状态和混沌状态下，零售商利润随公平关切水平变化的情景，可知零售商2考虑公平关切不利于供应链参与者利润最大化的实现且公平关切水平越高，利润损失越大。图18用三维网格图显示了零售商利润同时随价格调整速度和公平关切水平变化的情景，当λ,α3维持在较小数值时，系统利润平稳不变，随着两参数值的增大，系统最后陷入混沌状态且大部分利润值低于系统稳定状态利润值；因此零售商2在市场竞争中,保持参数值处于适当范围有利于自身利润的稳定和提高。

图16 α1=α2=0.5,α3=2.3时的利润动态图和随变化的平均利润图

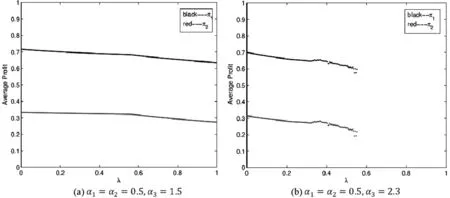
图17 零售商平均利润随公平关切水平的变化图

图18 零售商利润随λ,α3的变化图

结论5系统稳定状态的平均利润值大于系统混沌状态的平均利润值，零售商价格调整系数和公平关切水平过大不利于利润最大化的实现，零售商的价格调整系数应该控制在一定范围内，系统才能处于有序的竞争状态且有利于市场竞争者实现商业目标。

4 混沌控制

在零售商1和零售商2组成的寡头市场中，零售商的价格调整速度达到某一个临界值时，系统会出现混沌状态，此时系统处于无序状态且不可预测，零售商的价格和利润波动剧烈，甚至出现负值导致零售商的平均利润下降，对零售商的利润最大化目标很不利，因此零售商均有抑制竞争进入混沌状态的动机，所以需要运用一些控制方法使系统恢复稳定状态。

本文采用状态反馈控制的方法对系统(5)进行混沌控制，控制系统表示如下形式：

假设初始系统(5)表示为pi(i+1)=fi(p1,p2,p3)(i=1,2,3),其控制系统为：

pi(t+1)=(1-u)fi(p1,p2,p3)+upi(t)(i=1,2,3)

(8)

其中u是控制因子，可以认为是政府对价格调整速度的管制，或是市场竞争者的学习，市场适应能力；当u=0时系统(8)退化为系统(5)。

图19 控制因子u对价格动态博弈过程的影响

由图19的动态演化过程可知，当控制因子u达到某-数值时系统由混沌状态变为稳定状态，系统的混沌得到有效控制，零售商的利润同时也会整体提高。

5 结论

本文考虑零售商的不同的商业目标和公平关切行为，构建了双寡头零售商的动态价格博弈模型。运用非线性动力学和混沌理论对动态价格博弈模型的稳定性及参数对模型稳定性的影响进行了分析，得到以下结论：

(1)双寡头零售商竞争中，零售商拥有线下传统销售渠道和网上直销渠道时，考虑不同的商业目标会使其稳定域减小，系统中市场竞争减弱。

(2)在零售商双寡头市场中，零售商考虑公平关切时会使其自身的稳定域减小且公平关切水平越高，相应的稳定域越小，不利于市场竞争的稳定性。

(3)零售商在市场竞争中，价格调整系数应该控制在稳定域内，当某一零售商的价格调整系数超过稳定域范围时，即零售商的价格调整速度过快时，系统会出现分岔现象甚至陷入混沌状态。

(4)零售商公平关切行为会导致系统陷入混沌状态且公平关切的水平越高，系统越容易进入混沌状态。

(5)系统稳定状态的平均利润值大于系统混沌状态的平均利润值，零售商价格调整系数和公平关切水平过大不利于利润最大化的实现。价格调整系数越大，利润损失越大。

本文只分析了一个零售商考虑公平关切时的情景，现实中，双方零售商都有公平关切行为。考虑双方零售商的公平关切行为、顾客需求的不确定性和顾客的异质性等情景有待进一步研究。