非正态变异下的非线性轮廓异常点识别方法研究

聂 斌， 王 曦， 胡 雪

(天津大学 管理与经济学部，天津 300072)

0 引言

统计过程控制(Statistical Process Control, SPC)是质量管理领域的常用方法之一。此方法将统计技术应用于过程监控，通过分析工具观察过程的运行状态，对识别出的异常进行处理，以确保过程处于稳定、可接受的状态从而保证产品和服务的质量。

产品的质量特征由一元逐渐发展为多元，而且近年来轮廓型数据的监控问题已成为质量领域关注的热点问题。产品或过程的质量被描述为一个函数关系，其响应变量对应一个或多个解释变量。这种函数关系称为轮廓(profile)，或函数数据(Functional Data)。Woodall等[1]将轮廓监控分为两个阶段：第一阶段是以采集到的历史样本数据为基础，判断失控样本点并移除，建立稳定的状态模型；第二阶段是在第一阶段建立受控模型的基础上对实时数据进行监控，以及时发现过程中出现的变异。

本文研究的异常点识别问题属于轮廓监控第一阶段。由于第二阶段是根据第一阶段建立的模型进行实时判断，因此在第一阶段的模型中有效识别隐藏在所有观测点中的小部分异常数据点是非常重要的。异常点(outliers)通常预示着系统中的非正常状态，这些异常点可以提示一些有用的信息，甚至是能够有一些重大发现。关于异常点识别问题至今在各领域已有较多应用，如网络安全[2～5]，视觉监控[6,7]，遥感技术[8,9]，内科诊断学[10]等。

很多学者致力于线性轮廓异常点监控问题的研究[11,12]，而目前在医疗、工程、信息技术等领域的理论研究与工程应用方面，轮廓数据更多表现为非线性，即轮廓线的自变量与因变量之间的函数关系是非线性的。因此需要建立更加复杂的模型加以描述。不同学者在解决非线性轮廓异常点识别问题时提出了不同的方法[13,14]，很多数据处理技术被应用其中。当前研究多以随机变异服从正态分布为基本假设，然而在实际应用中大量存在非正态分布的情况，如经济指标多为偏态分布、产品寿命通常服从威布尔分布等。当正态分布假设不满足时，异常点识别性能会受到影响。

本文提出将小波分析、数据深度、聚类分析等技术相结合的非线性轮廓异常点识别方法，简称为WDC法。小波分析(Wavelet Analysis)是数据降噪的处理方法。数据深度(Data Depth)是一种通过对高维数据进行排序来描述数据的离心程度的方法。深度值越大，表示数据点越接近数据中心。聚类分析是依据数据自身的特征值将集合内的所有数据聚集为若干具有相似特征的数据类的方法。在以数据深度识别异常点的方法中均采用设定阈值的方法进行判定[15,16]，然而本文运用K-means聚类区分正常轮廓和异常点，经验证表明准确性更高。选择以上技术的另一个原因是其对正态分布假设的依赖性不强，应用范围广，经仿真验证在非正态分布变异下具有良好的性能。本文使用Matlab仿真的方法将新方法与Zhang等[20]提出的χ2控制图方法进行对比，结果显示新方法的性能更优。最后，采用木板垂直密度轮廓经典案例证明新方法在实际应用中是有效的。

1 数据模型及流程研究

假设研究对象是N条非线性轮廓，每一条轮廓线由M个点组成，每个点(xij,yij)是一个观测值，因此可以把这N条非线性轮廓看成N×M的矩阵。N条轮廓线所构成的样本均为随机抽样得到。轮廓线数据中包含正常轮廓线和异常轮廓线。每条轮廓线的一般函数表示为：

yij=f(xij)+εij

(1)

其中i=1,2,…,N；j=1,…,M；εij为噪声因子，εij∈N(0,1)。

当M的取值较大时，轮廓表现为高维特性。同时，非线性函数f具有相对复杂的特点。基于以上数据模型及非线性轮廓特点，本文提出的WDC法基本流程步骤如下所示：

第一步: 随机生成500条包含异常点的轮廓线，通过小波降噪的方法去除轮廓线中的噪声因子。

第二步：将降噪后的轮廓线通过马氏深度的方法转化为数据深度值。

第三步：对轮廓线对应的数据深度值进行K-Means聚类分析，取聚类数量为2，将数量较少的类做为异常点的集合。

当每条轮廓所包含的点的数量较大时，噪声因子将在很大程度上影响轮廓形状的变异性。因此，本文采用小波分析对原始轮廓数据进行降噪处理，尽可能降低噪声因子对异常轮廓线识别效果的影响。由于轮廓非线性函数的复杂性，无法以精确的函数模型描述其形状特征。因此，本文将轮廓视为高维空间中的点，并以其离心程度作为判断异常点的依据，从而实现在不需要对轮廓进行函数建模的前提下识别异常点。经典的多元统计方法在高维度的情况下效果受到一定的限制。当前普遍采用降维的方法进行预理，如变量选择法和投影法。然而，降维方法会造成一定程度上的信息损失，不能全面反映每个数据的变异。对于轮廓型数据，某些部分数据的变化表现为局部形状的变化。如果在降维过程中忽视了这些部分的变化，则不能准确的识别出表现为局部变化的异常轮廓。然而对于高维的非线性轮廓，局部变化是不能被忽视的，它是异常轮廓类型的重要组成部分。因此，本文利用数据深度中的马氏深度对轮廓的离心程度进行度量，能够有效避免信息损失。为了识别异常点，对转化后的数据深度值进行K-Means聚类分析。从高维空间上将异常点与占有绝对多数的正常点区分开来。最终实现对非线轮廓异常点的准确识别。

2 方法技术

2.1 小波降噪

小波降噪是小波变换在信号处理领域的重要应用之一，本质是抑制信号中的无用部分而增强信号中有用部分的过程。通常情况下实际测试中含有大量的噪声，这些噪声会影响到分析结果和分析精度，进而对得出结论的准确性产生影响，因此小波降噪处理是非常有必要的。

含有噪声的一维信号模型：

y(t)=f(t)+σe(t)

(2)

其中t=0,…,n-1，f(t)为真实信号，σ为噪声强度，e(t)为噪声，y(t)为含噪声的信号。信号的噪声一般情况下可以分为有色噪声和白色噪声两类。对于有色噪声的消除可以先采用对有色噪声白色化再按照白色噪声的方式进行处理。因此，小波降噪的重点在于消除信号中的白噪声[17]。

假设e(t)为高斯白噪声，则噪声强度为1。通常情况下有用信号表现为一些较平稳的信号或低频信号，而噪声信号表现为高频信号。

对混合信号y(t)消噪的目的在于消除噪声部分σe(t)，从y(t)中恢复出真实信号f(t)。小波降噪过程可分为三个步骤进行处理[18]：

(1)对信号进行小波分解，通过分解计算，分解为低频段和高频段；

(2)噪声因子通常在高频段信号中，因此对高频段信号以阈值量化等形式对小波系数进行处理；

(3)对信号进行小波重构以实现降噪。根据小波分解的低频段系数和高频段系数进行小波重构。

小波降噪步骤图如图1所示：

图1 小波降噪步骤图

2.2 马氏深度

数据深度通过对高维数据排序来描述数据的离心程度，以数据yi的深度D(yi)来描述yi在数据群中位置。数据深度越大，表示数据点越靠近数据群中心，数据点的信息量越大、重要性越高。目前，数据深度包含马氏深度(Mahalanobis depth)、半空间深度(Half-space depth)、空间秩深度(Spatial rank depth)、单纯性深度(The simplicial depth)。本文采用马氏深度法经测试有较好的性能。

马氏深度的提出源于马氏距离。设x,y∈Rd，则x和y关于正定矩阵Md×d的马氏距离为[19]：

(3)

定义x关于分布F的马氏深度(Mahalanobis)为：

(4)

亦可写作：

(5)

其中μF和∑F分别是对应于分布F的均值向量和协方差矩阵。

2.3 K-Means聚类

K-means算法作为经典的聚类分析算法中的一种，最早由MacQueen在1967年提出，目前是在众多领域应用较多的有效算法之一。K-means算法是根据样本的相似度将样本聚集到K个簇当中，使簇内样本相似度高而簇间相似度低。

给定一个包含n个d维数据点的数据集X={x1,x2,…,xi,…,xn}，其中xi∈Rd。K-means算法将该数据集划分为K类，C={ck,i=1,…,K}，每个类ck的质心为mk，选取欧式距离作为相似性和距离判断准则，计算各类总的距离平方和E(C)，聚类目标是使E(C最小。

(6)

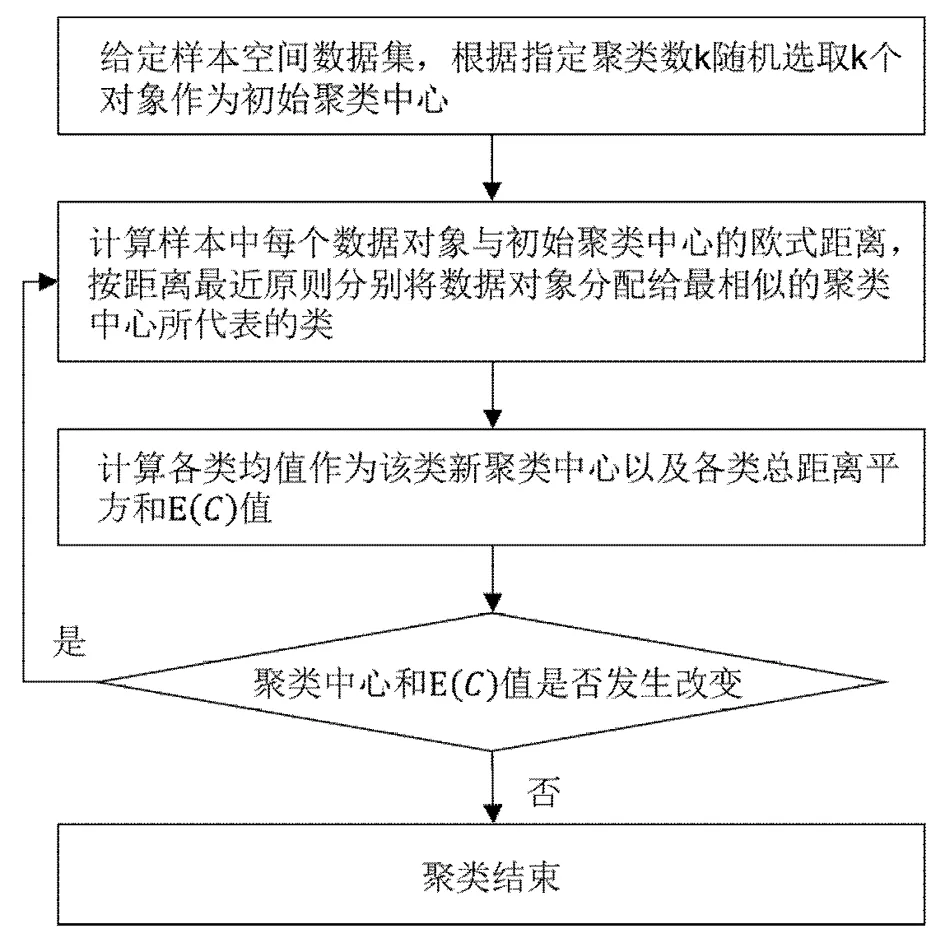
图2 K-means算法步骤流程图

3 性能分析

本文使用MATLAB对非线性轮廓异常点识别问题进行仿真并检测本文所提方法识别异常点的效果，并与Zhang等[20]所提出的用χ2方法进行对比。在本节依次介绍仿真过程、效果评价指标、仿真性能结果等。

3.1 仿真过程

在仿真过程中，首先生成随机的N条轮廓线，即N×M矩阵，然后进行小波降噪，减少噪声因子，进而运用马氏深度的方法以及K-means聚类将异常点识别出来。为保证方法的有效性，仿真生成500条轮廓线(包含正常轮廓和异常轮廓)用所提方法进行识别异常点。本仿真验证中以对数正态分布为轮廓的随机变异分布特征，目的是验证新方法对非正态变异的识别效果。以式(7)表示生成的正常轮廓曲线：

Y=3cos(x)+5sin(x)+εN

(7)

其中x∈(0, 2π)，εN为噪声因子，服从对数正态分布。εN的数学期望和方差分别为μN=0,σN=0.7，即ε服从期望为0，标准差为0.7的对数正态分布。

以式(8)表示生成的异常轮廓曲线：

Y=3cos(x)+5sin(x)+εA

(8)

其中x∈(0,2π)，εA为噪声因子，服从对数正态分布，σA=0.7。与正常轮廓线不同之处在于εA的期望μA是一个变化值，μA=0.1∶0.1∶2，即μA从0.1开始以0.1为步长，均匀取20个点至2止。图3展示出5条正常轮廓曲线和5条μA为0.5的异常轮廓曲线。

图3 轮廓线示意图

3.2 效果评价指标

在本研究中采用第一错误率(Type Error I)和第二错误率(Type Error II)作为异常点识别的效果评价指标。

第一错误率为生产过程中稳定过程被判定为不稳定的概率，即正常轮廓判定为异常点的数量与所有正常轮廓线数量的比值。

(9)

其中，M1为正常轮廓错判为异常点的数量；PN为正常轮廓数量。

相反，第二错误率为不稳定误判为稳定的概率，即异常点误判为正常轮廓的数量与所有异常点数量的比值。具体计算如下：

(10)

其中，M2为异常点误判为正常轮廓的数量；PA为异常点数量。

前文提到异常轮廓线的误差项期望μA是一个变化值，下节仿真结果将讨论随μA值逐渐增大，即异常轮廓线与正常轮廓线差异逐渐增大的时候，TypeErrorI、TypeErrorII如何变化。

3.3 仿真结果对比

为了探究在异常点数量不同的情况下，本文所提方法的性能效果的差异，本文引入异常点占比(记作Perc)指标，研究在异常点占总轮廓线比例(Perc)不同的情况下，异常轮廓线的误差项期望μA与TypeErrorI、TypeErrorII的函数关系。

仿真共随机生成500条轮廓线，考虑异常点占总轮廓线比例(Perc)分别为0.10、0.15、0.20这三种情况下，即异常轮廓线数量分别为50、75、100。按照本文所提方法在仿真中重复循环1000次，将本文所提方法性能与Zhang等[20]方法性能进行对比。图4展示的异常点占比(Perc)分别为0.10、0.15、0.20时μA与TypeErrorI对比图，实线表示本文所提方法，虚线表示对比方法。

图4 第一错误率性能效果对比图

表1为第一类错误的对比数据，由数据和图像可以得到以下几点结论：

(1)本文所提方法的第一类错误均明显小于对比方法；

(2)在μA相同情况下，对比方法的第一类错误和异常点占比(Perc)成明显反比，即TypeErrorI随Perc升高而减小。而本文所提方法在μA相同情况下，TypeErrorI随Perc升高而略有减小甚至变化不大；

(3)随μA增长，本文所提方法性能的差异性小于对比方法，说明本方法的性能在不同情况下具有一定的稳定性。

表1 第一错误率(Type Error I)性能效果数据表

图5 第二错误率性能效果对比图

图5展示的异常点占比(Perc)分别为0.10、0.15、0.20时μA与TypeErrorII对比图，实线表示本文所提方法，虚线表示对比方法。

表2为第二类错误的对比数据，由数据和图像可以得到以下几点结论：

(1)本文所提方法的第二类错误均小于对比方法；(2)在μA相同情况下，本文所提方法和对比方法的第二类错误和异常点占比(Perc)均成正比，即TypeErrorII随Perc升高而增大。

(3)异常点占比(Perc)不同时，本文所提方法的μA-TypeErrorII函数曲线变化幅度小于对比方法。即Perc不同时，本文所提方法性能稳定性优于对比方法。

表2 第二错误率(Type Error II)性能效果数据表

综上所述，经过仿真分析得到的性能对比结果可知，对于非正态变异的非线性轮廓线本文所提方法的第一错误率明显小于对比方法，第二错误率略小于对比方法。由此可知，本文所提方法在解决异常点识别问题时效果优于Zhang等[20]所提出的用χ2方法。

4 实例分析

在本节中，引入垂直密度轮廓(Vertical Density Profile, VDP)案例对本文所提方法的实际应用效果进行验证。本案例最先由Walker和Wright[21]提出，进而很多质量监控领域学者在研究过程中均对其进行分析，主要研究木板厚度方向上的密度变化。通常情况下，纤维木板为中间芯层断面密度高，两侧断面密度低。通常使用激光准确扫描模板各个位置的垂直密度来得到不同轮廓曲线。每张木板的垂直密度轮廓线体现了其产品质量水平。VDP数据共包含24条轮廓，每条轮廓线包含314个观测值。该24条轮廓线呈现出浴盆形态，如图6所示。

图6 VDP轮廓数据图

采用本文所提出的WDC方法对VDP数据进行异常点识别，利用Matlab软件进行分析计算，得到的结果为：轮廓线3、6、16、11、21为异常点。图7展示了VDP数据的异常点识别结果。由图像可看出，第3条、第6条轮廓线明显偏移整体轮廓线，第16条轮廓线整体位于偏下方的位置，偏离于主体轮廓线，故这三条轮廓线符合异常轮廓的特征。对于轮廓线11、21，可以看出这两条轮廓线的两端偏离于主体轮廓线的两端位置，轮廓线21两端高于主体轮廓线的两端而轮廓线11两端低于主体轮廓线两端，但是由于和主体轮廓形态没有明显差异，因此判定轮廓线11、21为疑似异常点。

图7 WDC方法识别出的异常点

5 结论及展望

针对非线性轮廓异常点识别问题，本文提出了基于小波降噪、马氏深度和聚类分析的WDC方法，此方法首次使用聚类分析识别转化为数据深度值的轮廓线中存在的异常点。通过MATLAB仿真测试新方法的性能并与χ2控制图方法对比。结果显示对于非正态变异的非线性轮廓新方法的第一错误率明显优于对比方法并且第一错误率随异常点占比改变变化不明显，同时第二错误率也优于对比方法。WDC方法在性能与稳定性方面均优于对比方法。

由于小波降噪、数据深度等技术仍有很多不同的方法，因此如何合理选择相应的技术，针对不同对象获得最佳的分析效果仍有待深入研究。另外，非正态分布的分布类型也有很多种，在对数正态分布以外的其他类型过程中本方法的性能表现仍有待研究。非线性轮廓的形态也会影响识别效果，因此仍有必要对新方法的适用性进行全面探讨。