基于贝叶斯学习模型的水权交易谈判议价模型与仿真
田贵良,韦 丁
(河海大学商学院,江苏 南京 210098)
1 概 述
1.1 水权交易及其定价方法
我国人均水资源量为2 300 m3,为世界人均水平的25%[1]。水资源短缺问题是我国急需解决的问题。水权交易是一种利用经济手段重新分配水权的形式,通过水权交易能够最大限度地实现水资源的合理配置。现阶段水权交易存在招标定价、拍卖定价和谈判定价3种主流市场竞价法,其中谈判定价机制简单明了,无需较多历史成交数据作为依据,提高了交易的灵活性,降低了交易成本,是目前最主流的水权交易定价方式。
1.2 水权交易方式及其价格形成综述
中国水市场正处于发展的初级阶段,水权交易的理论与实践也处于起步阶段,交易的运作机制和具体实施方式有待进一步研究。自浙江义乌开始水权交易以来,越来越多的学者开展了水权交易研究。水权交易中,价格是交易的动力及杠杆,价格的形成推动着交易的持续进行。陈洪转等[2]通过博弈论建立了水权交易博弈定价模型,同时解析了水权交易定价决策机制;唐润等[3]通过分析,确定了讨价还价是水权交易确定的有效途径;李长杰等[4]针对常见的水权交易,建立了水权交易买卖双方叫价拍卖的不完全信息博弈模型,确定了双方叫价拍卖机制;孙天昊等[5]提出贝叶斯分类增强学习策略,通过贝叶斯学习模型不断协商加快协商解的收敛,证实了策略的有效性;刘钢等[6]引入合作博弈理论,构建了水权交易下的动态博弈定价模型。
水权交易可以在交易所进行,也能够在线交易。目前,比较常见的交易方式如拍卖、竞标和讨价还价。拍卖交易意味着水权转让方将拍卖交易所持有的水权,投标人获得水权。议价模式是指交易双方最终通过协议达成的水权交易形式。谈判本质上是一个解决问题的过程,双方在谈判中共同寻找可能的解决方案的空间,并就冲突达成共识。在水权交易谈判中,双方共同关心的是交易给自身带来的利益规模。通过谈判,双方各自的收益不断波动,最终平衡在他们自己和对方的可接受范围内。交易双方谈判效用分析见图1。由于水资源特殊的自然属性、经济属性和社会属性,协商议价是当前及今后相当长时间内水权交易价格形成的主要模式。研究表明,现阶段大多水权定价研究是基于讨价还价及拍卖模型。本文将买卖双方作为核心要素,基于贝叶斯学习模型,通过谈判议价的模式,进一步确定各自风险及其报价,最终完成交易。

图1 交易双方谈判效用关系分析
2 基于贝叶斯学习模型的水权交易谈判议价模型
2.1 贝叶斯学习模型
贝叶斯学习模型是基于对方的报价序列,通过贝叶斯公式不断修正先验知识以更准确地掌握对方交易的价格底线。贝叶斯学习能够帮助交易双方在掌握对方信息不完全的情况下作出合理的报价决策,有利于双方效益最大化的实现。水权交易的根本目的是通过交易形式实现水资源的最优配置,若交易过程中双方信息不完全,谈判议价将导致报价不合理进而影响交易效率。贝叶斯学习能够在双方信息不完全的情况下对双方报价区间进行合理修正,保证最终谈判价格的合理性,提升交易效率。
贝叶斯公式可以表述为:存在定义的一组数量为n个的事件A1,A2,…,An,满足①P(Ai)>0;②Ai∩Aj=φ,i≠j;③∪Ai=Ω。
则贝叶斯公式定义为
(1)
式中:P(Ai)为先验概率;P(x|Ai)为条件概率,表示事件A发生条件下事件x发生的概率;P(Ai|x)为后验概率,是经过贝叶斯学习修正后对学习对象的认知[7]。
2.2 水权交易过程中的贝叶斯学习模型
在水权双边交易谈判过程中,水权交易的受让方与转让方准确知道自身可交易水量范围内水价的价格底线,但是他们并不知道对方交易价格的底线,因此需要做出估计,将该估计称为贝叶斯学习模型的先验知识,双方的报价可在谈判轮次中依托贝叶斯学习模型进行修正[8]。水权交易双方都有动力通过提高对方价格底线的估计价值来获得谈判过程中的优势。
在谈判议价的交易过程中,双方通过贝叶斯学习模型对于对方底线价格进行估计,随后基于对方的最大风险做出己方的谈判策略,进而在合理区间内做出让步。在经历N轮报价及让步后,最终双方谈判价格将收敛至合理区间,产生最终价格。在谈判过程中,重点在于底线交易价格确定及双方让步幅度计算,基于底线价格基础上进行报价的让步方能得出最终合理的谈判价格。贝叶斯学习模型机理见图2。
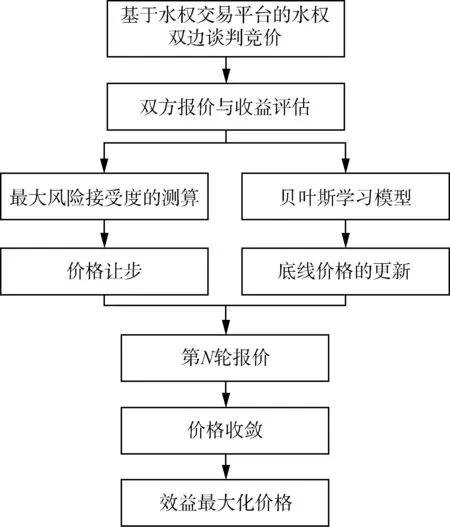
图2 贝叶斯学习模型机理
现从水权交易受让方角度分析转让方底线价格的贝叶斯学习过程。设转让方交易水价底线价格为λ,受让方对转让方交易价格底线的估计值分为I个区间,即受让方估计转让方有I个价格底线区间,第i个交易价格底线估计区间为i(i=1,2,…,I)假设在每个可能的区间[λi,λi+1]中服从均匀分布,其概率分布函数表示为[9]:
(2)
对应每个λi,受让方将转让方的水权交易的报价分成J个区间,转让方报价存在于第J个价格区间中的概率为pi,j(j=1,2,…,J)。
谈判开始前,受让方对转让方水权交易底线价格的期望为
(3)
当水权交易转让方报价后,受让方使用贝叶斯公式根据转让方的报价来更正最初估计转让方报价范围的概率分布。更正结果为
(4)
经过修正的受让方对转让方水权交易底线价格的估计平均值为
(5)
水权交易中受让方根据这种后验概率对第t+1轮投标作出决定,这也是在下一阶段学习的先验概率。
在转让方更新了该轮次报价后,受让方修正了转让方价格底线估算值的平均值。经过多轮谈判,受让方的估计值逐渐接近转让方的容量价格底线。在贝叶斯学习过程中,受让方和转让方根据彼此的报价调整自己对对方底线价格间隔概率分布的估计。
2.3 交易最大风险度
最大风险度反映了水权交易双方的收益风险[10]。最大风险度越高,风险越大,交易者在最终谈判交易中利益受损的可能性就越大。根据转让方报价,受让方对转让方进行风险评估,如果受让方的最大风险值较小,受让方做出让步让报价逐渐收敛;如果受让方最大风险度值较大,将不改变其初始价格。水权交易谈判议价过程中,交易各方不仅要计算自己的最大风险,还需要估计对方的最大风险以分析对方报价策略,进而基于对方的估计最大风险度确定己方谈判策略。
定义水权交易双方的最大风险度为
(6)
(7)
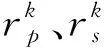
水权交易中受让方通过成本定价法得到交易收益函数表达式(式(7)),转让方的收益函数需要受让方通过贝叶斯学习模型不断纠正转让方报价进行估算,进而用估计的收益函数估算转让方最大风险度([0,1]之间)。由于受让方在谈判过程中无法知道转让方的准确价格底线和收益函数,因此转让方的初始价格估计在谈判的初始阶段可能与转让方的实际价格底线有很大的偏差,由此导致转让方的利润估计可能是负面的。所以在谈判开始时,r可能大于1。随着谈判的进展,受让方逐渐修改转让方价格底线的估算,r值最终回归[0,1]之间。
2.4 水权交易过程中最小谈判让步幅度
在水权交易过程中,水权交易双方均基于对方的报价对己方最大风险度进行估计,同时合理估计另一方的风险接受度。风险接受程度高的一方将通过修改自己的报价做出让步:


如果水权交易中谈判双方均认为己方风险度过高不作出让步,则谈判便无法继续甚至宣告破裂。经过上述周期循环,让步过程不断重复,双方基于对自己及对方风险度的估计做出价格的调整,最终使得双方风险接受度相同,报价向合理范围收敛并不断接近,直到双方在中间某一区域达成一致。用公式则表示为
(8)
此时受让方风险等于转让方风险,受让方与转让方同时做出让步,二者风险一致,就此达成一致的价格。
2.5 水权交易双方效益分析
水权市场是一个不完全竞争的市场,水权交易需要政府的宏观调控[11-12]。在综合考虑交易双方对水质和水量的要求后,交易双方才能进一步进行交易谈判。
2.5.1 水权受让方收益函数
在水价定价构成的体系中,参与者多种多样,包括但不限于政府、灌区管理单位、不同行业用水户等。
考虑到受让方多为企业单位,执行水权交易后,水权的购买能够为企业带来相应的收益,但同时也要考虑到购买成本、采水所承担的运费、水资源使用过程中所承担的污水处理费用。假设双方交易水资源量为q,交易价格为tb,输水单价为ts,污水处理单价为tw,可得:
Sp=Vp-Bp-CPY-CPW
(9)
式中:Sp为水权交易中水资源为受让方带来的净收益;Vp为交易量q下为受让方带来的收益,用函数fb(q)表示;fb(q)/q为单位水产值;Bp为交易量q下受让方所负担的成本,用qtb表示;CPY为交易量q下所承担的输水费用,用qts表示;CPW为交易量q下受让方承担的污水处理费用,用qtw表示。
综上,水权交易中受让方收益函数表达式如下:
Sp=fb(q)-q(tb+ts+tw)
(10)
2.5.2 水权转让方收益函数
由于转让方多为农村组织,假设出售水权后农业产值不发生变化,除此次水权交易为其带来的直观收益,还应包括初始取水成本及相应节水费用。
假设初始取水成本为tq,单位农业节水成本为tj。可得:
Ss=Vs-Csq-Csn
(11)
式中:Ss为水权交易转让方净收益;Vs为售水量q下的收益,用qtb表示;Csq为售水量q下的初始取水成本,用qtq表示;Csn为售水量q下的节水成本,用qtj表示。
综上,水权转让方收益函数表达式为
Ss=q(tb-tq-tj)
(12)
2.6 水权交易谈判议价的均衡价格区间
在公平的市场交易情况下,保持水权交易正常进行的前提是双方的收益为非负的,即Sp≥0,Ss≥0。交易中交易双方在考虑自身报价的同时也要考虑对方的价格承受范围,对于双方的出价范围,称之为可交易的最高价格与最低价格。
用Mpmax表示受让方允许的最高出价,Mpmin表示受让方允许的最低出价。因此受让方出价范围为区间[Mpmax,Mpmin];同理用Msmax表示转让方可接受的最高出价,Msmin表示转让方可承担的最低出价,转让方出价范围为区间[Msmin,Msmax]。交易双方报价最终收敛情况见图3。

图3 交易双方价格收敛
交易谈判中,受让方初始报价往往基于其最低出价,转让方初始报价往往基于其最高可接收报价,双方在交易中根据博弈的过程,受让方往往倾向于压低价格,转让方则选择提升价格。
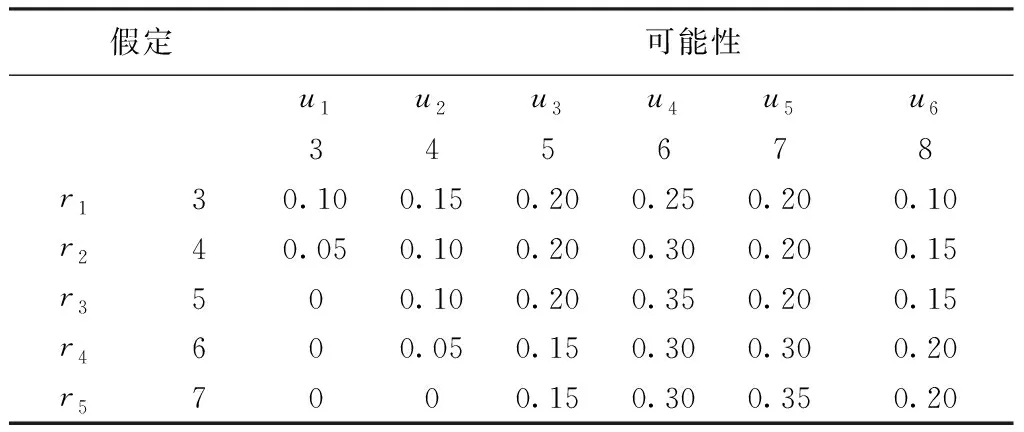
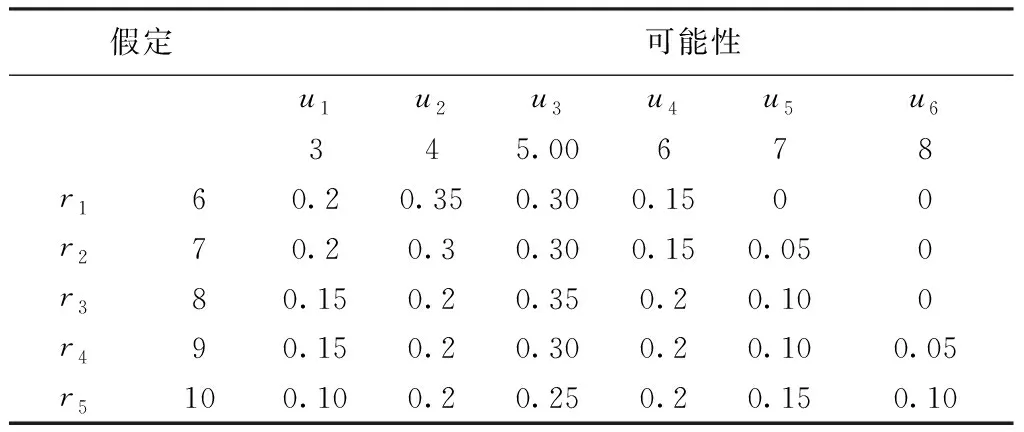
a.Msmax b.Mpmax c. [Mpmin,Mpmax]∩[Msmin,Msmax]=[Msmin,Mpmax]。买卖双方的报价均在合理的讨论范围内,转让方倾向于从Msmax进行出价,受让方则倾向于Mpmin进行出价;为了保证交易的正常进行,在不考虑双方坚持自身报价的条件下,受让方基于自身的出价及对对方收益的预估,往往倾向于压低对方出价,期望交易价格尽可能接近于Mpmin,同理,转让方则倾向于提升受让方的报价,期望交易价格更接近于Msmax,由此往复,使得双方报价收缩最终保持一致。为了保证交易正常进行,双方最终售价将收缩至[Msmin,Mpmax]范围内。 通过水权交易双方在交易中的经济效益分析,受让方期望掌握转让方的底线价值,转让方则想要掌握受让方的最高可接受价从而参与谈判。因此,在谈判开始之前,交易双方通过对对方底线价值进行估算,进一步掌握对方底线价格概率分布这一先验知识。通过先验知识的分析与自身交易底线价格的估计,进而做出决策。 Zeuthen策略通过最大风险接受程度,以确定一方是否做出了让步机制。在每一轮报价中,受让方和转让方都应计算自己的最大风险接受度,同时估算交易对手方的风险接受度。风险较小的一方将以最小的利润作出让步,从而确保谈判继续进行。交易双方在谈判过程中报价逐步收敛,当两者报价一致时得出最优解。 数据选取《大连市水资源合理配置及初始水权问题研究》中相关数据,水权交易量q在最大风险度的计算中可以作为除数约去,并不影响后续的实证分析,因此数据的选取不涉及具体交易量。参照文献[13],得到受让方单位交易水资源产值fb(q)/q=12.37元/m3,单位交易水资源输水费用ts=1.5元/m3,单位交易水资源污水处理费用tw=0.6元/m3;水权转让方单位取水成本tq=0.1元/m3,转让方单位节水成本tj=0.732元/m3。 受让方对转让方底线价格的估算见表1,表1中:①[ri]为对受让方底线价格的估算;②p(ri)为[ri]的概率估计,如p(r1)=0.1,p(r2)=0.25,∑p(ri)=1;③初始概率基于已完成水权交易数据估算而来,通过历史数据分布进而确定在不同区间内出现的报价概率。条件概率分布见表2,转让方底线价格更新见表3。 表1 受让方底线价格估算 表2 条件概率分布 表3 转让方底线价格更新 谈判前,受让方根据表1的先验知识可以估算出转让方的底线交易价格: R=∑ripi=5.05元/m3 转让方提交10元/m3的报价后,受让方根据表3进行贝叶斯学习并更新转让方的可交易底线价格。更新后,转让方交易底线价格为4.99元/m3。 转让方对受让方底线价格的估算见表4,条件概率估算见表5,转让底线价格更新见表6。 表4 转让方底线价格估计 表5 条件概率估算 谈判前,转让方根据表1的知识对受让方的底线价格估计为8元/m3。 受让方提出4元/m3报价后,受让方根据表6进行贝叶斯学习,并更新转让方的可交易底线价格。更新后,转让方交易底线价格为7.95元/m3。 表6 转让方底线价格更新 a. 受让方最大风险度的计算: b. 转让方最大风险度的计算: 由于水权转让方的最大风险度低于受让方的最大风险度,说明受让方风险承受能力较小,转让方承担的风险较小,则受让方会坚持报价,转让方进行报价的让步。 c. 最小让步幅度计算。为了推动水权交易的持续进行,水权交易转让方将做出最小让步,使得受让方在此次交易中承担的风险变小。转让方需要基于最小让步幅度进一步降低报价,使得转让方的风险与受让方风险保持在同一水平。 基于双方最大风险度估计,为了保证交易的正常推进,转让方将做出让步,根据最小让步幅度,转让方在第二轮报价中出售价格降至8.55元/m3,通过降低自身报价从而进一步降低受让方风险。 转让方进行价格让步后,受让方基于让步后的价格重新计算新一轮的最大风险接受度。 第二轮报价中,由于水权转让方的最大风险度小于受让方的最大风险度,说明受让方风险承受能力较小,转让方承担的风险较小,则受让方会坚持报价,转让方将做出最小让步,使得受让方在此次交易中承担的风险变小。转让方基于最小让步幅度进一步降低报价,使得转让方的风险与受让方风险保持在同一水平: 第二轮交易中,基于双方最大风险度估计,为了保证交易的正常推进,转让方将做出让步,根据最小让步幅度,转让方在第二轮报价中出售价格降至7.39元/m3,进一步降低受让方风险。 重复多轮贝叶斯学习和决策之后,直到达到满意的解决方案。 经过计算可得知,在第8轮计算时,水权交易买卖双方最终达成一致,最终价格为6.48元/m3,处于交易双方可接受区间范围内,买卖双方均可从此次水权交易中获取溢价收益。最终结果见图4。 图4 贝叶斯学习模型仿真价格收敛 水权交易双方通过水权交易将盈余的取水权转让,使得水资源利用效率达到最优。交易过程中通过谈判议价的方式实现,交易价格的高低决定了买卖双方的回报水平。如果任何一方在谈判过程中无法掌握对方的信息,就很难准确把握议价策略,导致不公平的谈判甚至交易中断。本文基于Zeuthen与贝叶斯学习的谈判模型,实例仿真结果表明:①通过贝叶斯学习,水权交易双方能够对对方可承受的最高或最低价格概率分布状况进行估计,在N轮次的议价中逐渐揭露对方交易底线,从而为估算对方收益打下基础;②通过对比水权交易双方风险,基于max风险接受度原则,风险较大的一方保留报价,风险较小的一方根据最小的让步幅度做出让步,以确保谈判能够持续进行,从而避免谈判破裂;③通过贝叶斯学习模型,经过双边谈判后,水权交易双方将报价逐渐收敛至双方可接受价格区间中,最终形成一致价格,从而结束谈判,完成此次水权交易。3 基于Zeuthen策略的水权交易谈判议价的仿真分析
3.1 受让方决策过程


3.2 转让方决策过程


3.3 双边学习


3.4 交易谈判结果

4 结 论

