基于博弈视角的三阶段流域水量冲突协调分配研究
陈军飞,裴金鹏
(1.河海大学商学院,江苏 南京 211100;2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)
流域水资源冲突是各利益主体因为对冲突的不同态度和决策而造成的紧张关系,其主要表现形式有水量冲突、水污染冲突等,属于复杂的系统问题,各主体及因素之间的互动交错又加剧了解决冲突的难度。近些年,极端干旱天气频发,2009—2013年连续5年长江流域云南地区均出现春旱,2015年夏季北方阶段性干旱突出,2017年黄河流域鲁东地区持续干旱,在此背景下,流域水量冲突问题引起了人们的密切关注。在新常态下,水利部、国家发展和改革委员会联合出台了《“十三五”水资源消耗总量和强度双控行动方案》,水利部门还提出了水权交易、“河长制”等管理措施来应对流域水资源冲突问题。
学术界关于流域水量冲突问题的研究,近年来在水量冲突协调模型与水量冲突管理对策两方面取得了一定的进展。在水量冲突协调模型方面,针对流域多主体取水冲突问题,有关学者考虑水量与水质两个因素,建立了多方博弈分析模型[1-2],考虑冲突参与人的行为构建了情景分析模型[3-4],考虑流域最小生态需水要求,构建了可持续发展模型[5]。针对跨流域水资源冲突问题,孙冬营等[6-7]基于模糊联盟合作博弈,研究了跨流域水资源二次配置模型,丰富了流域水资源冲突的理论方法,但都未考虑跨流域调水所产生的费用问题。Swatuk等[8-9]考虑水量协调分配过程中的冲突与合作,将基尼系数引入水资源分配模型中,对跨界水量冲突问题进行了进一步研究。在水量冲突管理对策方面,国外学者基于虚拟水视角对流域水资源高效利用进行了研究[10-11]。国内学者对国内外水资源管理制度的历史沿革进行了梳理,从流域水资源政策制定角度为水量冲突管理提供借鉴[12-14]。Alison等[15-16]提出了一项新的水资源管理计划,通过衡量各取水者对水资源总量的贡献,来确定取水主体的取水量。该计划可以平衡不同取水主体的利益,有助于解决流域水量冲突问题。
已有关于水量冲突问题的研究,多应用单一的博弈模型,很少对多种博弈模型进行对比,较少考虑水资源冲突过程中涉及的不同用水主体之间的关系,应用于具体案例的也不多。本文在前人研究的基础上,应用三阶段流域水量协调分配博弈模型,研究流域水量协调分配过程中利益主体间的关系以及其决策,并对具体案例进行分析,为管理者协调流域水量冲突提供决策参考。
1 问题概化与模型假设
1.1 问题概化
流域水量冲突问题涉及方面较多,在跨界时尤为复杂。因水量协调分配过程中自流域上游到下游,流域内的各主体都有可能参与,各主体会基于个体理性做出决策,并且会随着其他主体的决策改变对策,不断变化,最后形成各自的决策,这是一个典型的博弈问题。
图1为某流域n个地区取水的关系图,地区1~n按该流域的走向分别表示流域内n个取水主体。设该流域可取水总量为q;用ω1,ω2,…,ωn分别表示各地区从该流域的取水量,易知q=ω1+ω2+…+ωn。
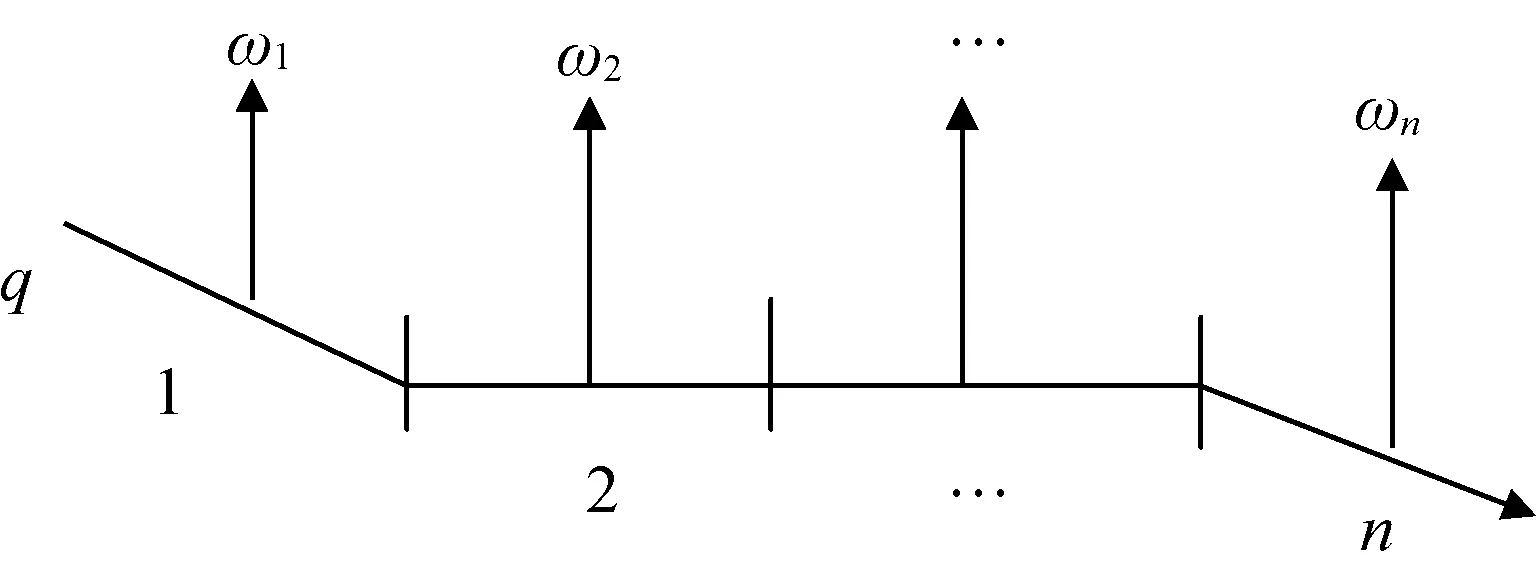
图1 流域水量分配示意图
假设整个流域水量分配博弈有n个参与者,该博弈分配问题可用以下博弈模型来描述:
a. 参与者集合N={n个地区};
b.n个参与者的行动集分别为X1,X2,…,Xn;
c.n个支付函数Π1,Π2,…,Πn,其中Πi(X1,…,Xn)表示当参与者1采取行动X1,…,参与者n采取行动Xn时,参与者i所得到的支付;
d. 流域水量协调分配对策记为S={n,{Xi},{Πi}}。
1.2 模型基本假设
a. 假设Bi(x)表示i地区的用水收益,其中x为有效用水量,包括取水量ωi以及节水量ϖi。Bi(x)与x呈抛物线关系,且用水边际收益呈递减趋势。
b. 假设Ci(ωi,li)表示i地区的取水总费用,Ci(ωi,li)与ωi直接相关,其中li表示i地区能够获取水量的上限。ωi受li的限制,自流域的上游到下游,水量的递减会导致边际取水费用递增。

Wk=(ω1,ω2,…,ωn)T
2 三阶段协调分配模型
流域水量冲突问题涉及流域各利益相关者,其协调分配是一个复杂的博弈过程。
2.1 阶段一:个体理性的非合作博弈
早期流域内各用水主体对水量冲突问题的态度以“自利”居多,由于缺乏相关的法律法规支持,各用水主体各行其是,许多决策之间无法协调,使得水量的分配整体上是失衡的。该阶段各用水主体的决策往往只关注输入而忽视输出,因此建立基于个体理性的非合作博弈模型,来展现流域各用水主体基于个体理性的行动与决策过程,全面分析该区域的水量分配状态。
为了简化模型,假设整个流域可取用水总量q是地区1决策的唯一影响因素,其他地区则分别以经过其上一地区的剩余可取水量作为决策的依据。效益函数为
(1)
各地区的决策以效益最大化作为共同目标,即:
(2)
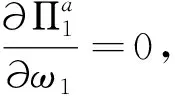

约束条件为
(3)
求得决策向量:
2.2 阶段二:集体理性的合作博弈
基于个体理性的非合作博弈,由于地理位置的差异,各用水主体必然存在利益冲突,影响流域的整体利益。因此建立基于集体理性的合作博弈模型,即流域管理者首先发布配水的指令,流域内各地区用水主体进行取水决策时,为了达到预定的目标,就会寻求与其他地区合作,从而实现全流域效益目标的极大化。
设各地区的效益函数与阶段一一致,但此时需引入政府调控作为影响因素,流域管理者制定各地区生产生活的基本用水量qi,影响各用水主体的决策,使得在水量分配的过程中,整个流域的效益最大化。即:

(4)
(5)
(6)
约束条件为
(7)
式中q1,q2,…,qn表示地区1,2,…,n的基本用水量。
由式(5)(6),可以求得集体理性的合作博弈水量分配对策为
2.3 阶段三:政府与市场相结合的合作博弈
阶段二的目标是达到集体理性,但由于决策者首先考虑的是流域整体效益的最大化,而作为方案接受者的各地区,其考虑的则是个体效益的最大化。这一矛盾无法消除,导致集体理性的合作博弈模型很难达到均衡。新常态下,市场是最有效的资源分配方式,在市场中个体与集体之间能够实现利益相容,二者在理性方面并非完全对立。所以阶段三在阶段二的基础上引入水资源税、水权交易等行政与市场手段,共同完成水量协调分配任务。
设水资源税与用水量成正比,税率为t,同时在各地区之间分配全流域的水权。假设ri表示地区i分配到的水权,p表示市场中的水权交易价格,则各地区的效益函数变为
(8)
其约束条件为
(9)
式中q1,q2,…,qn分别为地区1,2,…,n的基本用水量。
行政与市场共同协调下各地区的决策及求解过程为:




3 案例分析
3.1 参数确定及计算
根据《常德年鉴》《湖南省水资源公报》以及《湖南省“十三五”水利发展规划》,估算出常德市澧水流域的总供水能力约为30亿m3,多年平均流量约为5亿m3。考虑数据的可得性,确定函数参数时主要考虑有效用水量、取水量和节水量。
设Bi(x),i=1,2,3分别表示石门、临澧、澧县地区的用水收益,x表示有效用水量。利用澧水流域流经常德石门、临澧、澧县地区2011—2016年的经济资料与有效用水量,拟合用水收益函数为
(10)
假设Ci(ωi),i=1,2,3分别表示石门、临澧、澧县地区的取水费用,ωi表示取水量。利用澧水流域流经常德各地区2011—2016年的取水量与取水费用资料,求得3个地区的取水费用函数为
(11)
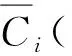
(12)
a. 阶段一:由式(9)、式(10)及式(11),求得澧水流域常德段的水量分配结果如表1所示。

表1 个体理性的非合作博弈模型水量分配结果
b. 在阶段二的调配中,必须保证各地区的基本用水量。根据《常德市水利“十三五”发展规划》,估算其分别为1.089亿m3、11.351亿m3、2.466亿m3,考虑各地区的最大可能节水量,根据《湖南水利年鉴》等资料取最大值,其分别为0.936亿m3、7.019亿m3、2.367亿m3,求得澧水流域常德段的水量分配结果如表2所示。

表2 集体理性的合作博弈模型水量分配结果
c. 阶段三:在设定条件下,求得t+p=1.78,故澧水流域常德段的水量分配结果见表3。

表3 政府与市场相结合的合作博弈模型水量分配结果
3.2 结果分析与建议
由表1可知,各用水主体在确定自己的取水量和节水量时有以下特点:地区1完全依据自己的需求、效益函数来进行决策;地区2则根据地区1的ω1得到该地区的来水量,即q-ω1,再以此为前提来确定自己的ω2和ϖ2,地区3与地区2的决策过程相似。所以阶段一,澧水流域各地区的用水对策是一个顺序决策问题,易引发冲突。如表1的分配结果显示,地区1、2为追求自我利益,使得地区3无法满足基本用水需求。上游用水主体相对下游用水主体具有位置优势,故流域管理者不能放任各用水主体自由取水,需进行协调分配,避免水量冲突。
由表2与表1对比可知,阶段二相对于阶段一而言,其主要的改进有两点:①节水水平有了很大的提高,有助于提高全流域的整体效益。②阶段二引入政府调控作为影响因素,会保障各地区的基本用水需求,不会出现地区3无水可用的情况。所以,阶段二的分配效果更佳,即全流域的效用更优。但是阶段二在求最优解时存在前提条件,只有当流域管理者掌握所有用水主体的真实效用函数信息时,才可以利用阶段二模型进行流域水量协调分配,实现效益最优化。但在实际配置时,决策者首先考虑的是流域整体效益的最大化,而各用水主体基于个体效益的最大化,会隐瞒或虚报自己的用水效益函数,流域管理者很难获悉全部信息。这一矛盾无法消除,则集体理性的合作博弈模型很难达到均衡状态[17]。故流域管理者应多实地调研,组织专家测定,尽可能多地获取各用水主体的用水效益信息,对水量冲突进行协调分配[18]。
表3表明,阶段三各用水主体的节水量ϖ、取水量ω,均可用p+t来表示。即各用水主体会根据p和t的变化,确定预期决策。流域管理者在决策前,应明晰水权并建立合理的水市场,然后根据各地区的预期行动策略决定t,同时市场会做出反应,得到p。t和p都是公开信息,博弈过程中,流域管理者处于领导者的地位,而其他用水主体相当于追随者,因此,阶段三是广义的Stackelberg博弈,也是完全信息动态博弈。该模型能兼顾个体理性与集体理性,流域管理者可以根据t和p,有侧重地采取不同手段,对水量冲突进行动态协调。
5 结 语
a. 阶段一,流域各个用水主体和管理者都关注各自的效益最大化,流域各地区间的博弈是一个顺序博弈,处于上游的地区具有优势,下游的用水主体不能满足基本的用水需求,从而引发水量冲突,不符合流域的整体利益。
b. 阶段二相对阶段一,其主要的改进有以下两点:①模型二是基于政府调控,从流域整体利益出发,秉持集体理性,能保障各地区的基本用水需求;②节水水平有了很大的提高,提高了全流域的整体效益。但由于信息不对称,很难获得各用水主体的真实效用函数,个体利益与整体利益会出现冲突,使得阶段二很难达到均衡状态。
c. 阶段三在阶段二的基础上引入t和p两种手段,博弈过程中,流域管理者处于领导者的地位,而其他用水主体相当于追随者,并且信息是公开的,是广义的Stackelberg博弈。该模型能兼顾个体理性与集体理性,由于各利益主体的节水量ϖ与取水量ω均是关于p和t的函数,所以流域管理者可以根据t和p,对水量冲突进行动态协调。
建立三阶段流域水量协调分配博弈模型时,在目标函数方面,除了考虑用水效益,还可以考虑如环保效益等更多的目标;在指标方面,除了考虑取水量、节水量等,也可以考虑如排污指标、节水效率等指标,使博弈模型更加完善。

