超声波处理对麻竹笋干复水特性的影响及动力学模型

王昱圭，汤雪纤，刘思媛，张甫生，郑炯*

1(西南大学 食品科学学院，重庆，400715)2(西南大学，食品科学与工程国家级实验教学示范中心，重庆，400715)

麻竹笋被称为“寒士山珍”，含有丰富的营养成分，是深受现代人喜欢的纯天然绿色食品[1]。目前，竹笋的主要加工和保藏方法为干燥、腌制、盐渍和罐制等[2]。而竹笋经干燥后制成的笋干复水时间长，复水程度难以掌握，复水后笋干营养损失大，限制了笋干产业的进一步拓展[3]。

果蔬复水性受复水工艺条件的直接影响[4-5]。目前，果蔬复水的方法较为单一，主要是清水浸泡，并通过改变温度来控制复水时间，如用热-冷-热的复水方式复水薇菜干[6]，或加入一定化学试剂来提高复水效果，如用碱液处理来改善豌豆的复水效果[7]。但均存在复水耗时过长且复水后的品质受到了一定影响的问题。超声波是指高于人体听力阀的声波(>18kHz)[8]，其与媒质的相互作用可分为热效应、机械效应和空化效应3种[9]。谷物或豆类食品如糙米[10]、鹰嘴豆[11]、海军豆[12]、高粱[13]等，在经超声波复水后均有效缩短了其复水所需的时间，并在一定程度上提高了食品的品质。同时，超声波处理用时短、绿色低耗能[14]。因此，超声波在促进干物质的复水中具有较好的应用前景。

研究发现，超声波预处理可明显缩短香蕉片冻干总时间和提高成品复水率[15]；不同功率的超声波预处理对罗非鱼片复水率、质构和水分状态及其分布等都存在着一定的差异，且均优于无预处理的对照样品[16]。干制海参在经超声波处理后能够明显地提高复水速率，将泡发时间由2～3 d缩短至6 h以内，且随着超声波功率的提高、超声波频率的降低，海参的复水率和持水率增加[17]。目前，超声波用于干制品复水的报道大多与谷物食品和干制海产品相关，而关于超声波辅助复水麻竹笋干的研究报道较少。此外，复水动力学模型的建立可对食品复水过程进行有效地预测和描述，如Weibull模型能有效的描述干燥猕猴桃片的复水动力学[18]，挤压方便米饭的复水动力学过程可由线性方程进行描述[19]。因此，本文以麻竹笋干为研究对象，研究不同温度以及不同功率的超声波处理后的笋干复水特性，然后对麻竹笋干复水过程进行动力学模型拟合，确定最适宜的动力学模型来预测笋干的复水特性，以期为笋干的复水加工提供理论依据。

1 材料与方法

1.1 材料与试剂

麻竹笋干 采购于重庆市北碚区天生菜市场。

1.2 仪器与设备

JY98-IIIDN超声波细胞粉碎机，宁波新芝生物科技股份有限公司；JA5002型精密分析电子天平，上海精天有限公司；HH-8数显恒温水浴锅，常州澳华仪器有限公司。

1.3 实验方法

1.3.1 超声波处理

参考黄旭辉[17]方法并加以改动，取麻竹笋干中段部位，尺寸为1 cm×1 cm，约1g。6个样品为一组，放于500 mL保温杯中，加入不同温度(50、70、90 ℃)的400 mL去离子水，将直径为2 cm的探头伸入水中距离样品约1～2 cm，放好样品后将细胞破碎室密封。选定超声功率为0 W的麻竹笋干为对照组，其余样品选用5种不同的超声波功率(100、200、300、400、500 W)处理，超声频率为25 kHz，超声处理时的工作时间5 s，间歇10 s。每20 min取出笋干测量质量，共超声120 min。超声处理过程中每隔20 min更换去离子水，使水温基本无变化。

1.3.2 复水比测量

参考黄旭辉[17]方法，笋干复水前分别用分析天平测量其质量并记录。复水后，用吸水纸轻轻擦干笋干表面的水，并称量笋干复水后的质量。依照公式(1)计算出笋干复水比：

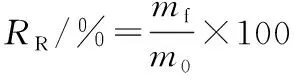
(1)

式中：RR，复水比；mf，笋干沥干后的质量，g；m0，笋干复水前的质量，g。

1.3.3 复水速率

参照许牡丹等[20]的方法，复水速率是指物料的平均干基含水率随时间的变化，复水速率按公式(2)计算：

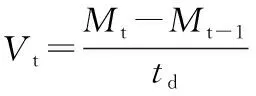
(2)

式中：Vt，复水速率，g/(g·min)；Mt，笋干在t时刻的干基含水率，g/g；Mt-1，笋干在t-1时刻的干基含水率，g/g；td，t-1时刻和t时刻的时间间隔，min。

1.3.4 复水过程数学模型

数学模型常用于描述食品干燥和复水过程中水分的变化规律，主要分为经验模型和理论模型。目前为止，还未见对超声波辅助麻竹笋干复水的数学模型研究的报道。因此，本实验选用了单项扩散模型、Page模型、Weibull模型对麻竹笋干的复水过程进行拟合，以期找出最适合描述超声波辅助麻竹笋干复水的数学模型，为笋干的实际加工提供理论依据。

1.3.4.1 单项扩散模型

单项扩散模型是简单的指数式模型，主要用于模拟干物质的复水或脱水过程[21]，其方程式为(3)：

Mr=αe-kt

(3)

将单项扩散模型的方程线性化后得(4)：

-lnMr=kt-lnα

(4)

式中：α、k为模型参数；Mr，水分比；t，超声波处理时间。

1.3.4.2 Page模型

Page模型是广泛应用于模拟食品复水或农业物料干燥的过程[22-23]，属于经验模型，应用在本文的方程式为(5)：

Mr=αe-ktn

(5)

将page模型的方程线性化后得(6)：

ln[-lnMr]=lnk+nlnt

(6)

式中：Mr，水分比；t，超声波处理时间；n、α、k，模型参数。

1.3.4.3 Weibull模型

Weibull模型属于半经验模型，被广泛应用于农产品干制品的复水模型[23-25]，其方程式为(7)：

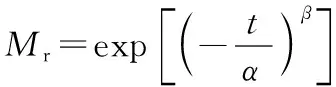
(7)

将Weibull模型的方程线性化后得：

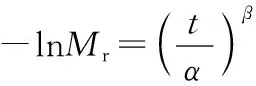
(8)

式中：Mr，水分比；t，超声波处理时间；α、β，模型参数。

1.4 数据处理

实验结果以“平均值±标准差”表示。所有实验均进行3次重复。应用SPSS 19.0统计软件，对数据进行方差分析。用Origin 8.0进行图表绘制，复水数学模型的拟合用SPSS 23进行，用R2来评估模型与实验数据的拟合程度。使用Duncan法比较平均值之间的差异性。

2 结果与分析

2.1 超声波处理对麻竹笋干复水特性的影响

2.1.1 超声波处理对麻竹笋干复水比的影响

图1为不同温度下超声波处理对麻竹笋干复水比的影响。在3个温度条件下，超声波处理后笋干的复水比都显著高于对照组(P<0.05)。且随着超声波功率的增大，复水比也增大。相关研究报道过超声波处理能够大大提升糙米[10]、鹰嘴豆[11]、海军豆[12]、高粱[13]、海参[17]等的复水比，与本文研究结果相似。这可能是因为超声波的空化效应和机械效应改变了食品内部细微的组织结构，使其具有小而密集的孔状结构[17]；同时，超声波也能减少笋干复水过程中的对流传质阻力[25]，使水分子更易进入组织细胞内部。相同功率下，随着温度的升高，麻竹笋干的内部组织更为疏松[26]。笋干的复水比也在显著升高(P<0.05)。因此，在较高温度下，大功率超声波处理能有效提高麻竹笋干的复水比。

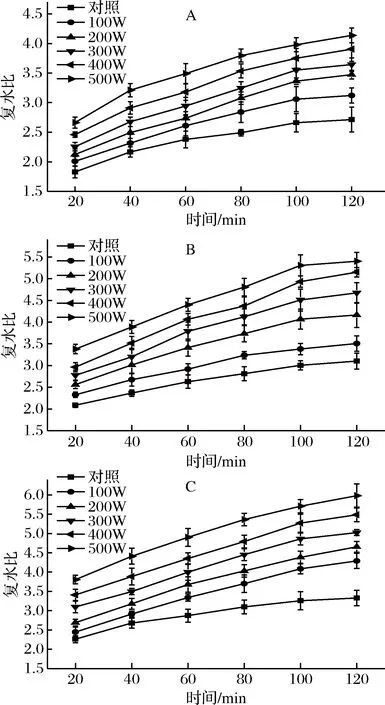
A-50 ℃;B-70 ℃;C-90 ℃图1 超声波处理对麻竹笋干复水比的影响Fig.1 The effect of ultrasound on the rehydration ratio of dried Ma bamboo shoot

2.1.2 超声波处理对麻竹笋干复水速率的影响

图2为超声波处理对麻竹笋干复水速率的影响。在相同温度下，超声波处理对笋干的复水速率可分为2个阶段，在复水初期时，笋干的复水速率较快；在水分含量达到平衡时，复水速率显著降低(P<0.05)且趋于平衡；并且随着超声波功率的增大，复水速率显著增大(P<0.05)。说明超声波功率的大小对笋干复水速率有一定的影响，且在复水初期时影响最大。这可能是由于超声波促使笋干内部组织结构发生了一定的改变，使笋干在复水初期具有较强的吸水力。当笋干中的水分含量达到一定程度时，吸水力减弱，复水速率的变化差异不显著(P>0.05)。同时，在相同超声波功率下，随着温度的升高，笋干复水初期时的复水速率显著增大(P<0.05)。这可能是因为细胞膜的通透性随温度的升高而增加[27]，使水分能加速进入细胞内部，说明温度的升高可提高笋干的复水速率。因此，超声波处理以及升高温度能有效提高笋干的吸水能力。

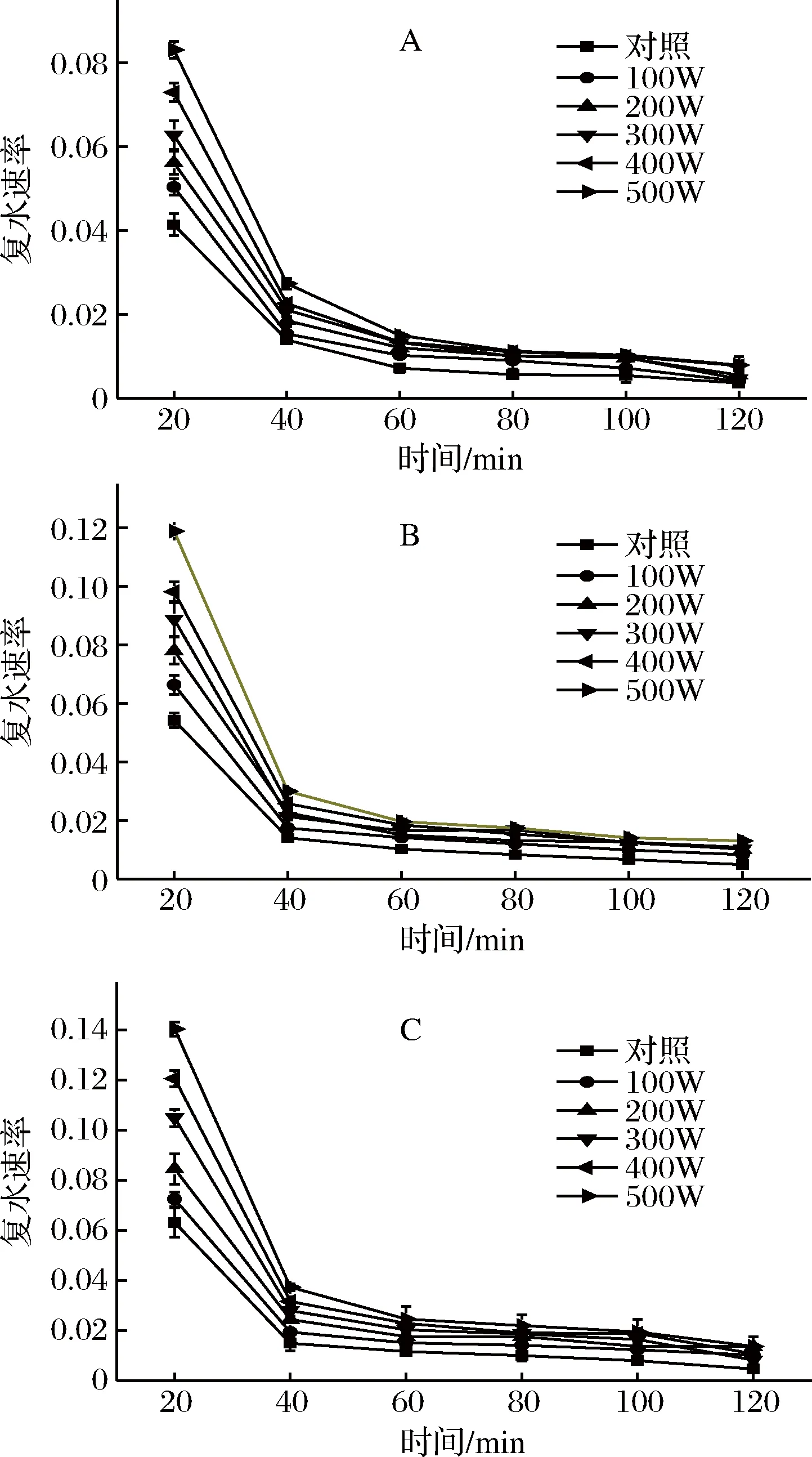
A-50 ℃;B-70 ℃；C-90 ℃图2 超声波处理对麻竹笋干复水速率的影响Fig.2 The effect of ultrasound on the rehydration rate of dried Ma bamboo shoot

2.2 复水动力学模型

2.2.1 单项扩散模型

表1为单项扩散模型拟合参数。50 ℃时，k值在超声波功率为200 W时达到最大。70 ℃时，k值在超声波功率为300 W时达到最大。90 ℃时，k值在超声波功率为200 W时达到最大。由此可见，单项扩散模型的拟合参数k是随着功率的增大呈现先增大后减小的趋势，且均大于对照组中的k值。同时，相同温度下，α值随着超声波功率的增大而减小，且均小于对照组。随着温度的升高，相同超声波功率下，α值减小，在温度为90 ℃，超声波功率为500 W时,α值最小。但笋干的复水过程并不能单纯地描述为简单的指数模型。而且单项扩散模型的R2值并不理想(R2>0.90),也说明单项扩散模型并不适合用于描述笋干的复水过程。

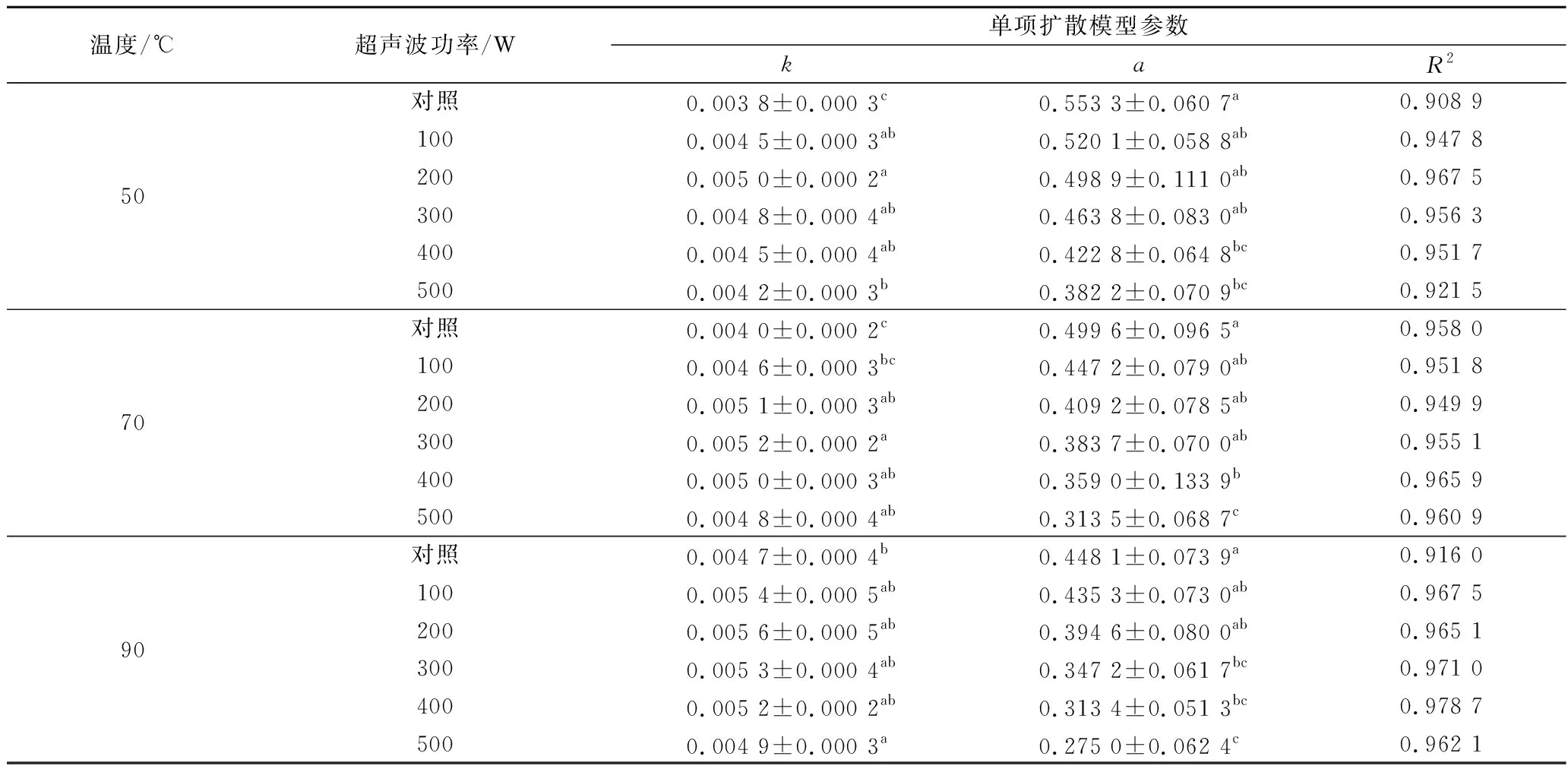
表1 单项扩散模型拟合参数Table 1 The single diffusion model fitting parameters

2.2.2 Page模型

表2为Page模型拟合参数，50 ℃时，n值随着超声波功率的增加而减少，在500 W时达到最小值。而k值则随着超声波功率的增大而增大，在500 W时k的最大值为对照组的2倍左右。70 ℃和90 ℃的条件下均有此规律。说明在相同温度下，随着超声波功率的增大，Page模型参数n值减小，k值增大，超声波功率为500 W时对n值和k值影响最大，且Page模型对k值的影响比对n值的影响大。

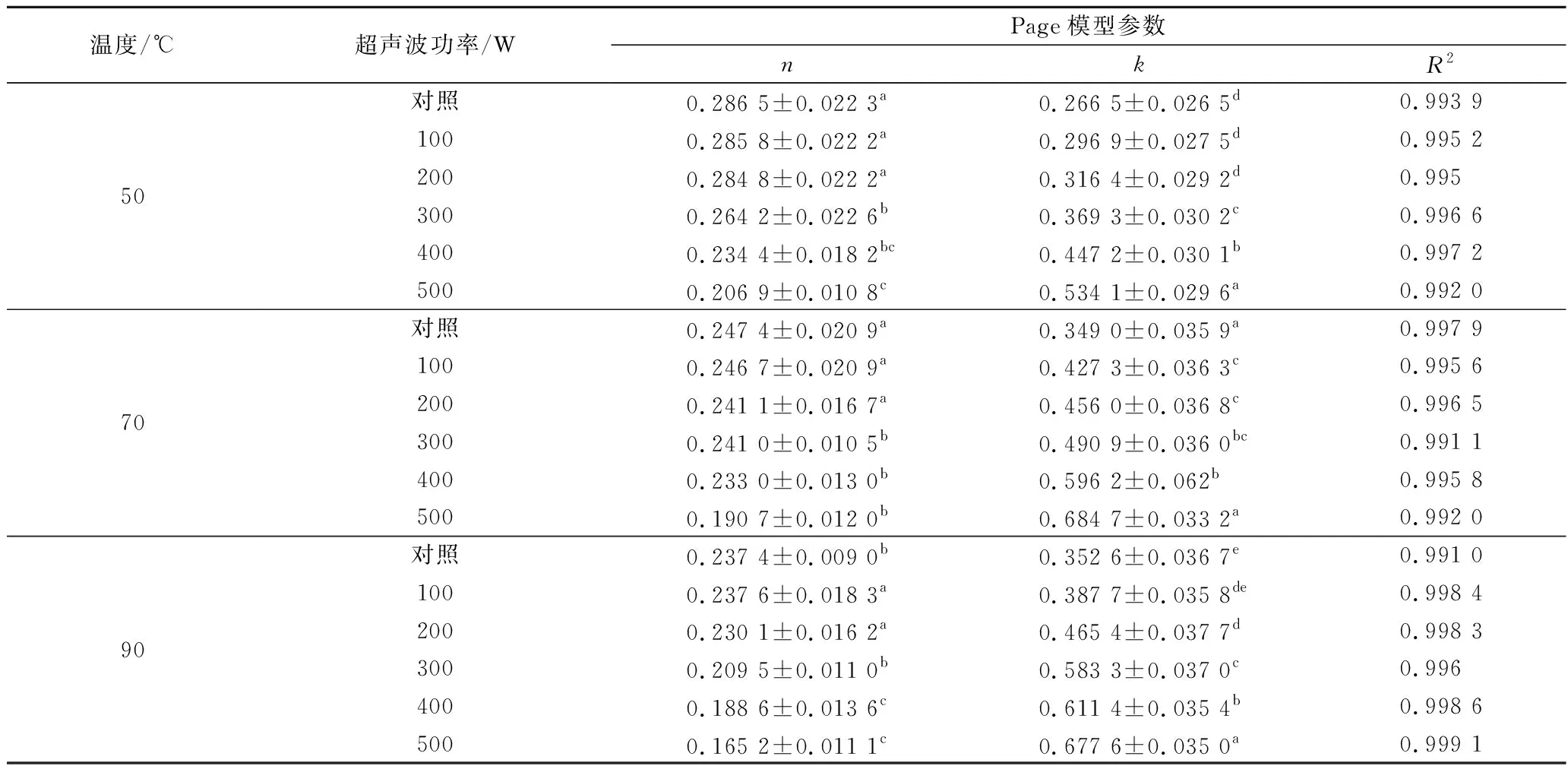
表2 Page模型拟合参数Table 2 Page model fitting parameters

在相同功率下，随着温度升高，n值减小，k值呈现出先增大后减小的规律。表明温度为70 ℃时，对k值影响最大。与单项扩散模型相比较，Page模型的R2值更接近1(R2>0.99)，说明Page模型能较好地描述笋干复水过程。

2.2.3 Weibull模型

表3为Weibull模型拟合参数。在Weibull模型中α被定义为完成63%水分吸收所需要的时间[28]，β与复水速率相关，β越大，吸水速率越小[29]。相同温度下，α值和β值随着超声波功率的增大而减小，且α值减小程度较明显。表明相同温度下，笋干完成63%水分吸收所需要的时间在减少，笋干吸水速率随着超声波功率的增大而增大，且超声波功率对α值的影响较为明显。这与黄旭辉的结论一致[17]。高功率的超声波能够有效地促进海参复水相同。在相同功率下，随着温度的升高，α值在大幅减小，β值减小程度较小，说明温度也可促进笋干复水[30-31]，且温度对α值的影响较大。从R2值可以看出，Weibull模型能够对笋干复水进行拟合(R2>0.98)，但与Page模型相比，其拟合度仍稍差。

通过表1、表2、表3的R2值的比较可以得出，单项扩散模型的R2值最小(R2>0.90)，不适用于对笋干复水过程的描述，Page模型的R2值最大(R2>0.99)，最适合用于描述和量化笋干复水过程。

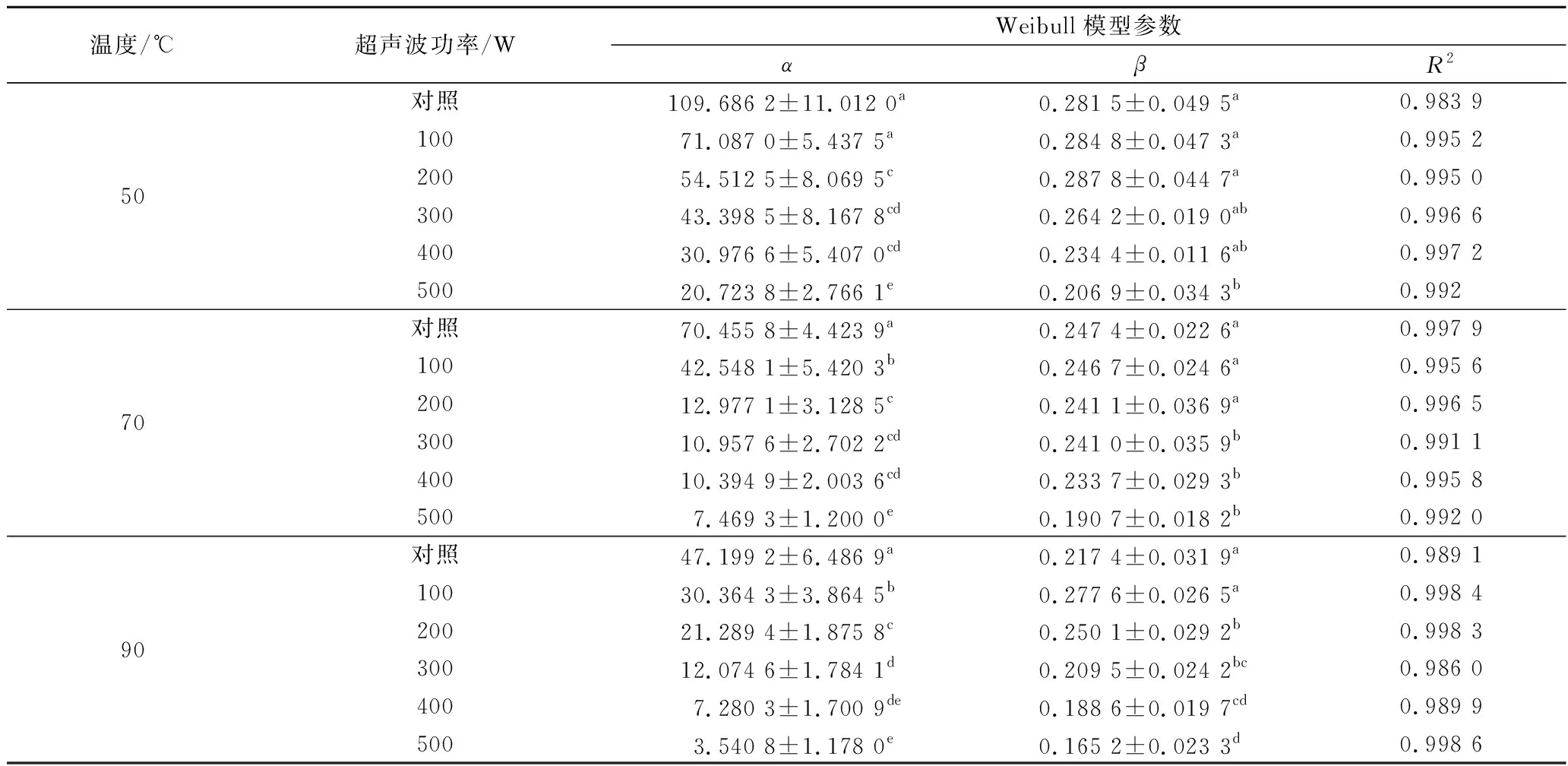
表3 Weibull模型拟合参数Table 3 Weibull model fitting parameters

2.3 复水动力学模型的验证

图3是不同温度下Page模型ln(-lnMr)的预测值与实测值的关系图。

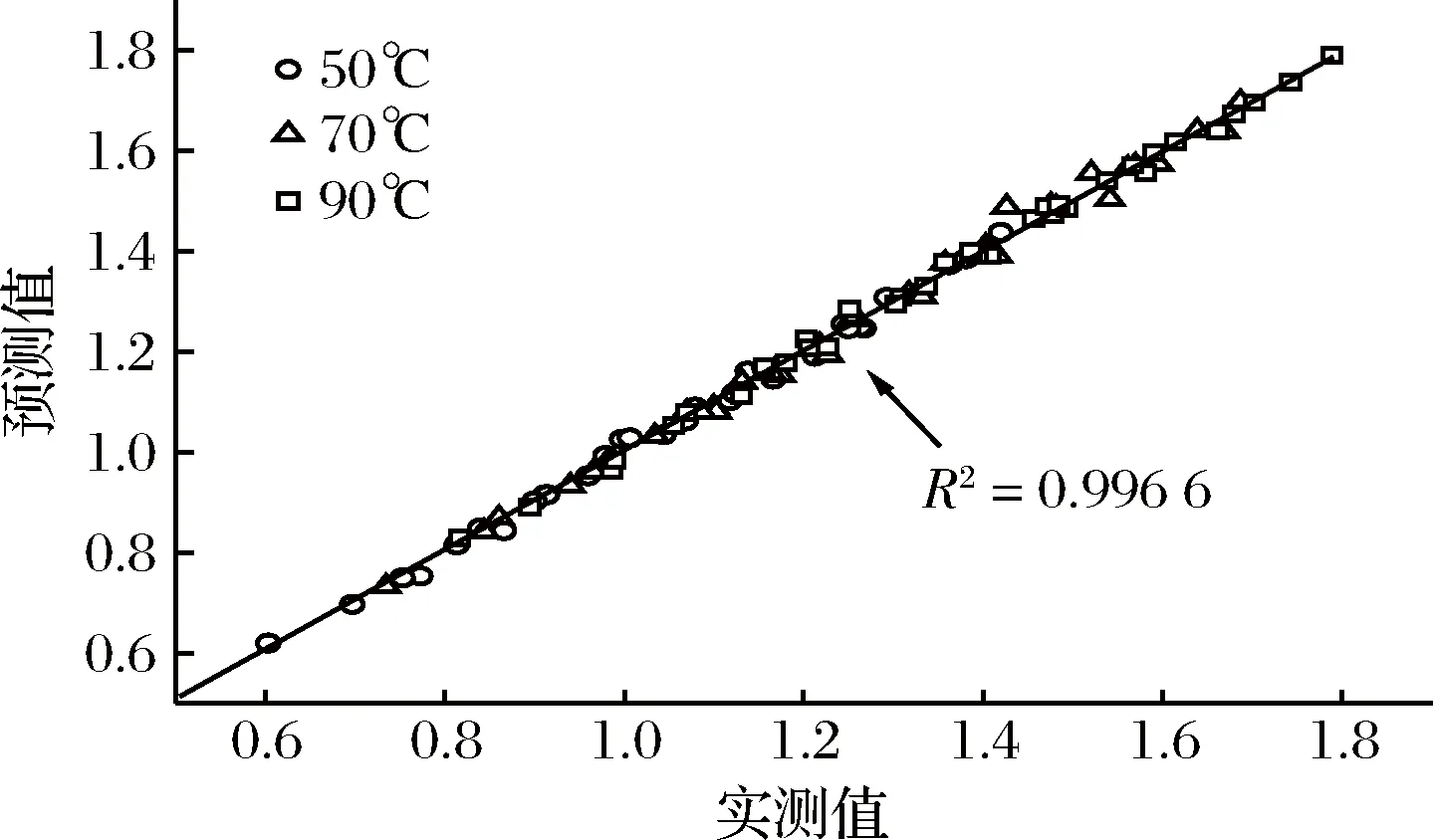
图3 Page模型预测值与实测值的比较Fig.3 The comparison between the predictive value and measured value the of Page model

Page模型在50、70、90 ℃时的预测值与实测值拟合度较高，说明Page模型能准确描述超声波处理笋干复水的水分变化过程，这一模型可以为实际生产过程中预测和寻求超声辅助麻竹笋干复水的最佳工艺条件提供参考。

3 结论

超声波处理能有效提高麻竹笋干的复水比和复水速率。随着温度的上升以及超声处理时间的增加，效果则更加明显。同时，对麻竹笋干的复水进行动力学模型拟合，结果表明Page模型具有较高的线性拟合精度(R2>0.99)，能较好地描述和预测不同温度下超声辅助复水麻竹笋干的过程。因此，应用超声处理可提高麻竹笋干的复水特性，为笋干加工提供理论基础及科学依据。