冷加工过程中316L奥氏体不锈钢硬度压痕尺寸效应分析
薛 河 李 凯 王 帅 赵 宽
西安科技大学机械工程学院,西安,710054
0 引言
316L奥氏体不锈钢具有优良的耐腐蚀性和良好的焊接性[1],常作为核电结构(焊接接头、管道)常用材料,在加工、安装过程中易产生“加工硬化”现象[2],其力学性能也随“加工硬化”过程发生变化,严重影响了核电结构完整性评价与寿命预测。近年来,人们常借助无损、快捷的压入法来获取材料的力学参数[3-4]。但大量研究显示,通过压入法获取材料力学参数时,硬度会在一定载荷范围内随着载荷的变化而变化,即出现硬度压痕尺寸效应(indentation size effect,ISE),严重影响材料力学性能的评价[5-6]。针对此问题,已有许多学者总结研究出许多定量或者半定量的理论模型来对此现象进行解释,常见的有比例试样阻力(proportional specimen resistance,PSR)模型、修正比例试样阻力(modified proportional specimen resistance,MPSR)模型、多重因子比例(multifractal scaling laws,MFSL)模型[7]。材料不同,适用的模型不同,ISE现象消失的临界载荷也不相同。蒋付强[8]通过对无应力状态下的3J21合金进行纳米压痕试验来研究压痕尺寸效应,引入常用的压痕尺寸效应描述模型,分析压入深度的变化对3J21合金硬度的影响规律,并确定利用纳米压痕测试微冲裁件残余应力的合适压入深度。许泽建等[9]通过对0Cr18Ni10Ti不锈钢焊接接头的显微硬度研究,得到接头各区域的显微硬度在较小的载荷下随实验载荷的增大而减小,当载荷超过1.96 N时,各区域硬度值基本保持不变的结论。房永强等[10]通过对钴基合金显微硬度测量压痕尺寸效应分析发现,引起硬度荷载依赖性的物理量与表示硬度荷载无关的常量成反比,与Meyer硬度指数n有关。
本文通过室温加载速率为2 mm/min下的单轴拉伸试验实现冷加工过程,分析了不同伸长率下316L奥氏体不锈钢基本力学性能参数的变化规律,通过室温下维氏硬度试验结合不同ISE理论模型讨论了316L奥氏体不锈钢ISE与伸长率的关系,并得到了维氏硬度真实值。随后对其结果进行了实验验证,最后通过得到的真实硬度值对维氏硬度测试过程中ISE现象消失的临界压痕载荷进行了确定。
1 物理试验
1.1 室温静态单轴拉伸过程及结果
试验材料选用车间批量生产的316L奥氏体不锈钢,其熔点为1 390 ℃,化学成分见表1。按照GB/T 2039—1997标准,通过卷板机将板材轧制成2 mm厚的钢板,在剪板机上裁剪成400 mm×400 mm方块,随后利用线切割机对其进行慢走丝线切割,最后打磨毛刺,加工后的几何尺寸如图1所示。在PLD-50 kN电液伺服疲劳试验机上(图2)按照GB/T228.1—2010标准,采用室温加载速率v=2 mm/min进行单轴拉伸试验,实现伸长率为0、15%、30%、40%(形变量分别为0、3 mm、6 mm、8 mm)的冷加工预变形,如图3所示。对不同伸长率下的316L奥氏体不锈钢进行单轴拉伸直至断裂,并借助UT7116Y型静态应变数据采集仪对标距段应变进行实时采集,试验过程符合GB/T228—2002标准,为了消除试验结果的随机性,本文通过三组试验进行说明,结果见图4和表2。
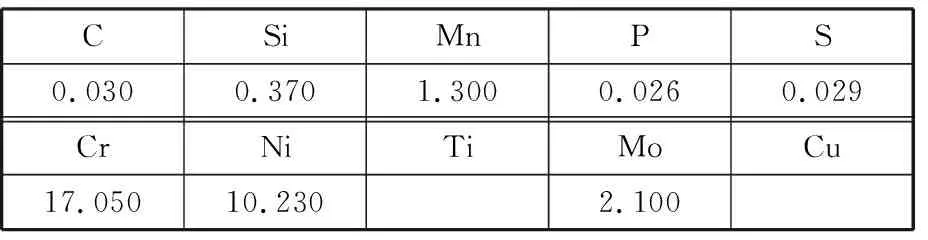
表1 316L奥氏体不锈钢主要化学成分(质量分数)
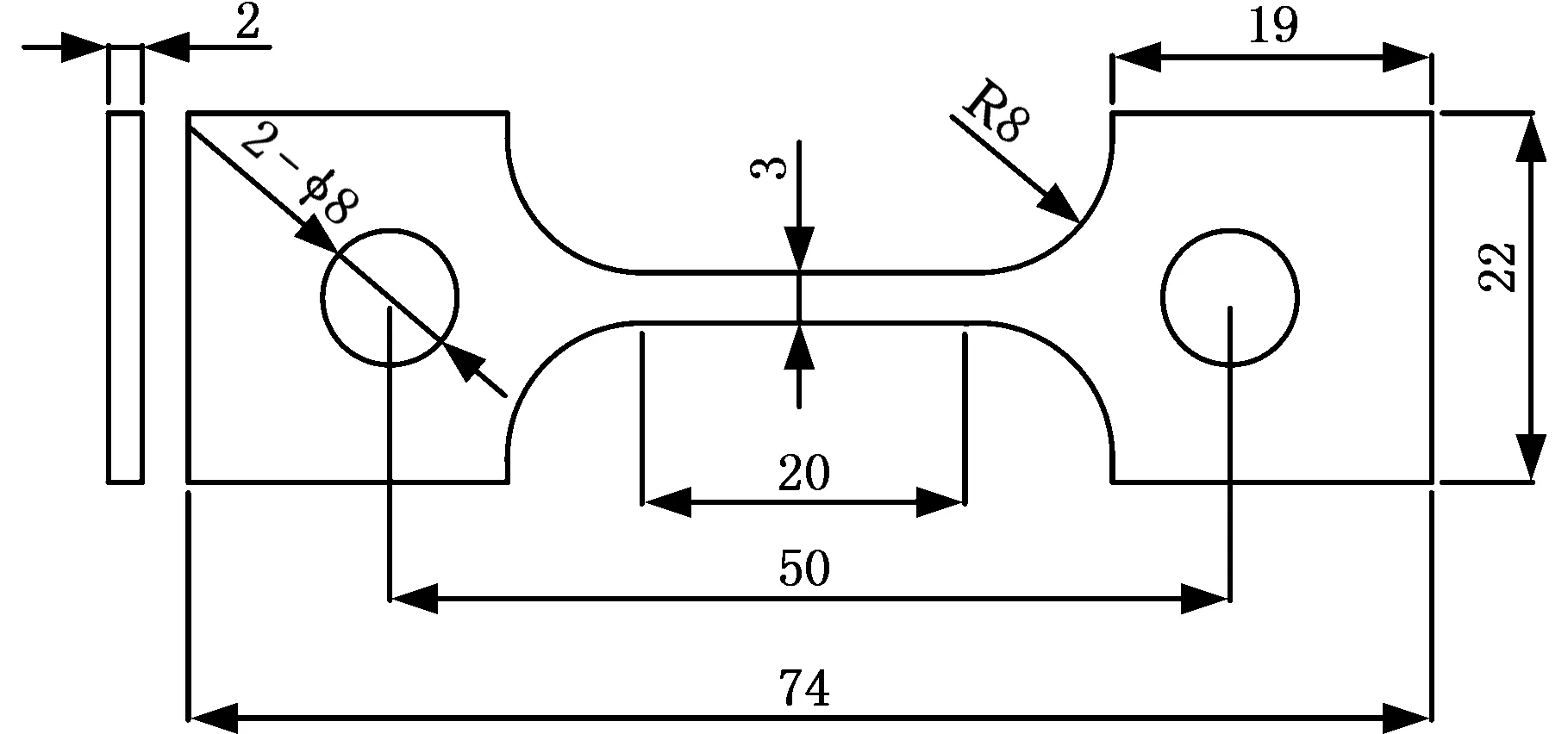
图1 平板拉伸试样几何尺寸Fig.1 The flat tensile specimen geometry

图2 PLD-50 kN电液伺服疲劳试验机Fig.2 PLD-50 kN electro-hydraulic servo fatigue testing machine

(a)第一组 (b)第二组

(a)第三组图3 不同伸长率下的316L奥氏体不锈钢平板试样Fig.3 The 316L austenitic stainless steel plate specimens at different stretching rates
1.2 维氏硬度测试试验
维氏硬度测试过程依据GB/T4340.1—1999,测试原理见图5。图5中压头为两面夹角α=136°的正四棱锥,材料为金刚石,为提高试验的准确性,测试前采用YMPZ-1金相试样自动磨抛机对不同伸长率下的平板试样(图3)表面进行打磨、抛光处理,随后利用HVS-1000Z型数字显微维氏硬度计对其进行硬度测试。整个试验在室温下完成,加载载荷依次为0.098 N、0.245 N、0.490 N、0.980 N、1.960 N、2.940 N、4.900 N。

(a)第一组 (b)第二组

(a)第三组图4 不同伸长率下的316L奥氏体不锈钢平板试样单轴拉伸断裂结果Fig.4 Uniaxial tensile fracture results of 316L austenitic stainless steel plate samples under different tensile rates
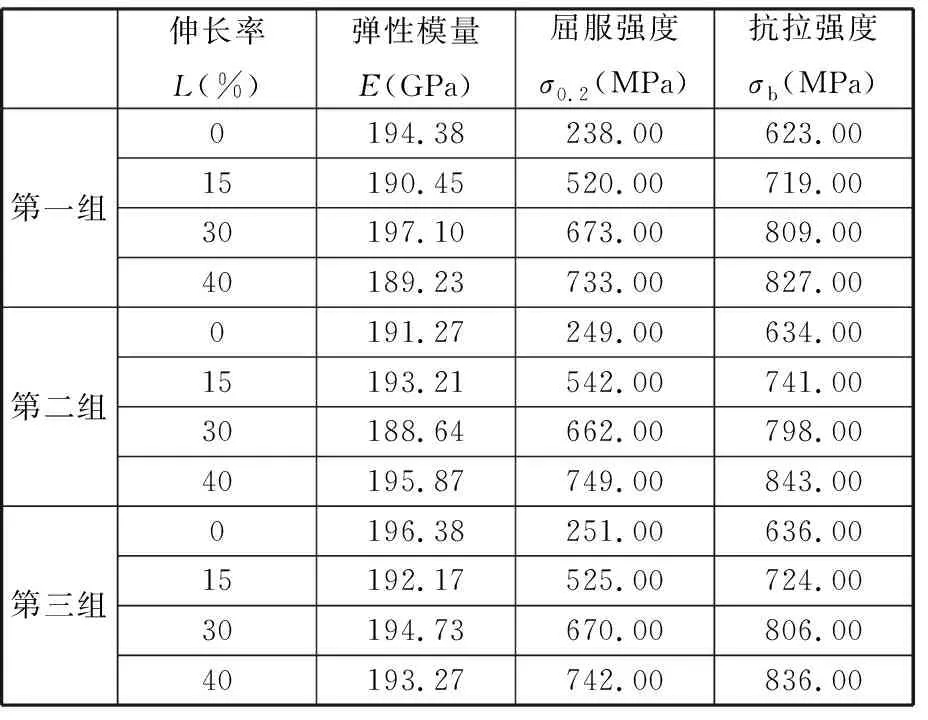
表2 室温静态单轴拉伸试验数据(v=2 mm/min)
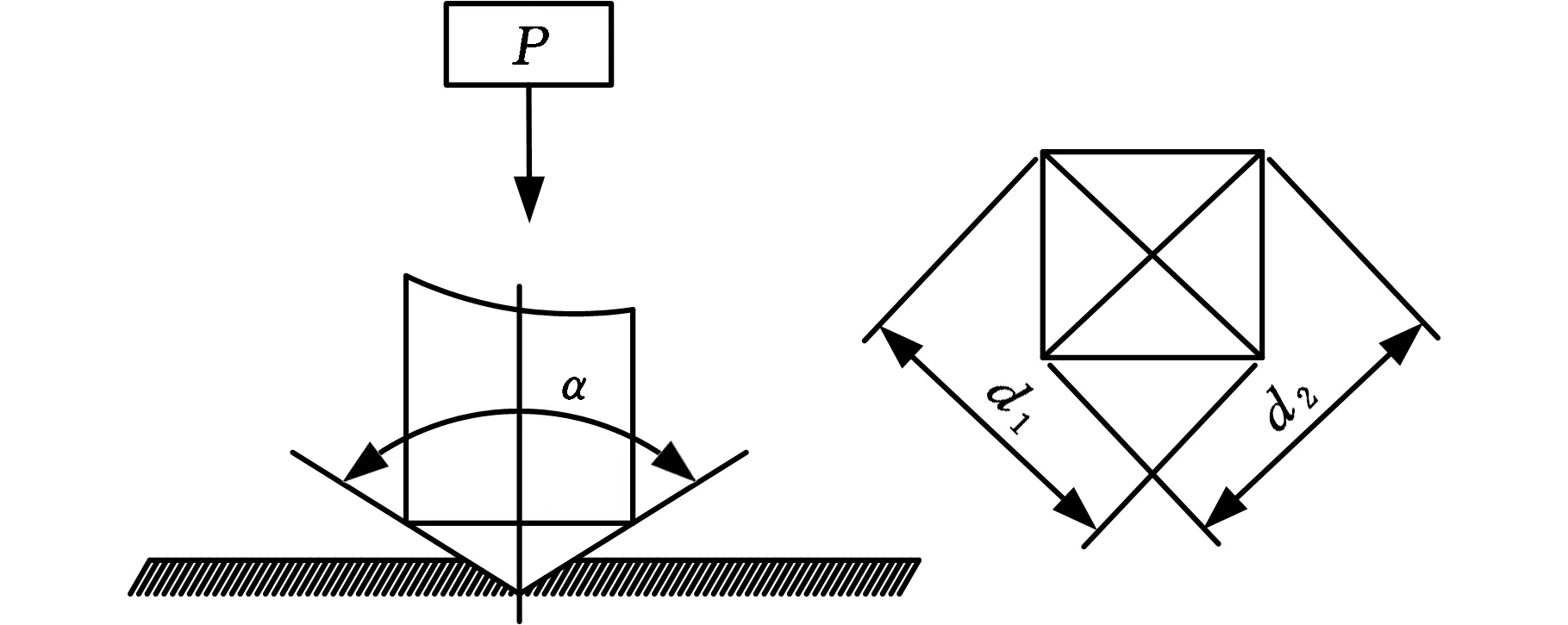
图5 维氏硬度测试原理Fig.5 Vickers hardness test principle
有压痕硬度计算公式[11]为
(1)
式中,H为硬度值,MPa;P为压头载荷,N;A为压头完全卸载后的面积,mm2;K为压头几何形状系数,通过试验数据拟合得到。
压痕硬度对角线长度平均值计算公式[12]为
(2)
式中,d为压痕对角线长度平均值,mm;d1、d2分别为压痕两条对角线长度,mm。
当压头完全卸载后,将压痕对角线长度d1、d2代入式(2)中计算出平均值,然后通过式(1)得到材料的硬度值。
2 结果讨论与分析
2.1 不同伸长率下316L奥氏体不锈钢基本力学性能变化规律
由于各组试验结果相近,为了使研究过程简便,本文在第一组试验结果基础上进行力学性能分析。不同伸长率下316L奥氏体不锈钢屈服强度与抗拉强度分布情况如图6所示。从整体来看,随着伸长率的增大,由于加工硬化现象的影响,屈服强度与抗拉强度均增大,而拉伸过程中加工硬化率受硬化机理的影响,随着形变量的增大,增大的趋势逐渐减小,因此会使得强度增大的梯度逐渐减小,尤其在伸长率大于30%以后呈现明显的减小趋势。
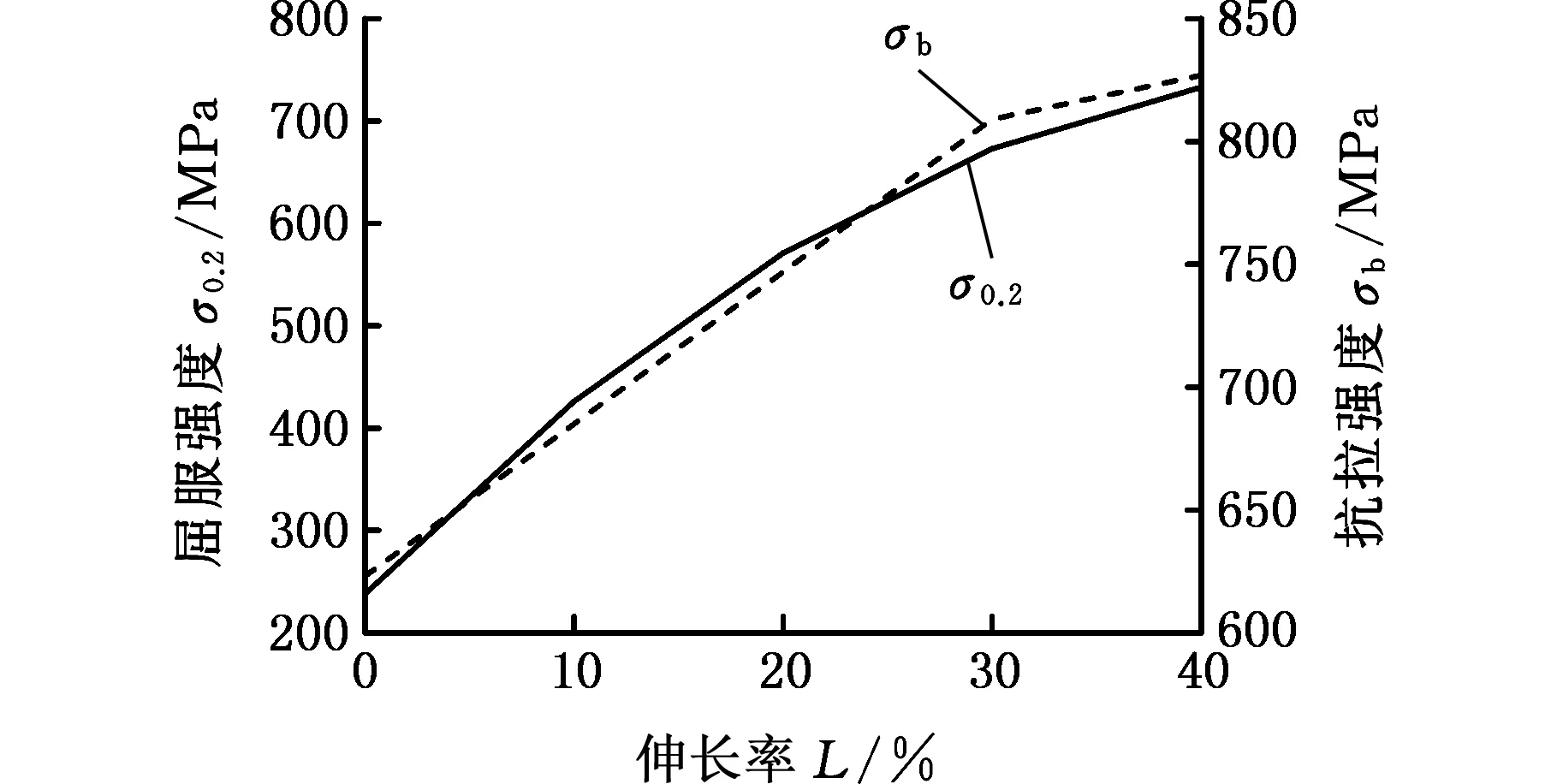
图6 不同伸长率下316L奥氏体不锈钢屈服强度与抗拉强度分布Fig.6 Distribution of yield strength and tensile strength of 316L austenitic stainless steel under different stretching rates
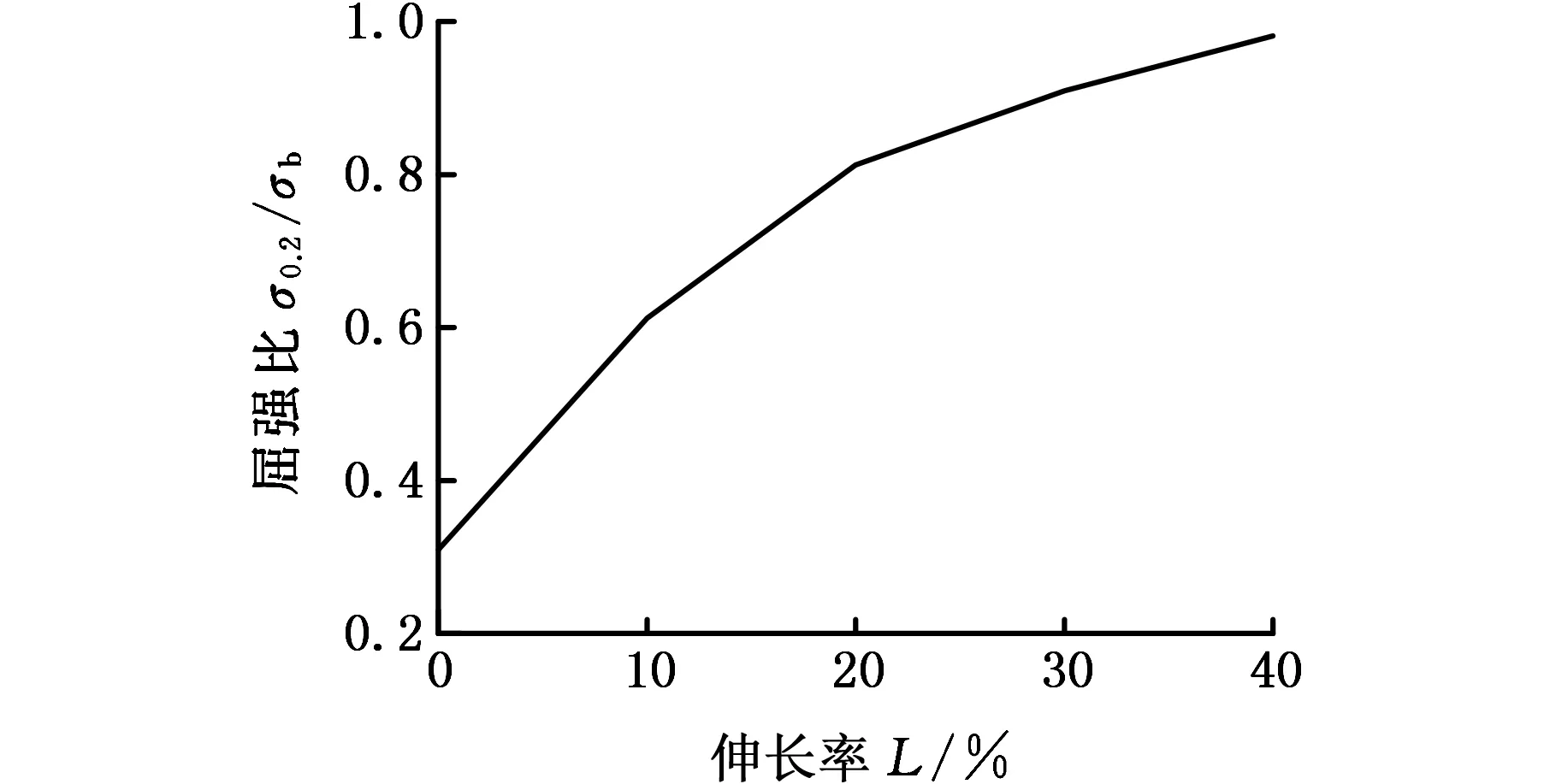
图7 不同伸长率下316L奥氏体不锈钢屈强比分布情况Fig.7 Distribution of yield ratio of 316L austenitic stainless steel under different stretching rates
屈强比是用来衡量材料强度储备能力的系数,用屈服强度与抗拉强度的比值来表示。316L奥氏体不锈钢屈强比随伸长率的变化规律见图7。从图7中可以看出,随着伸长率的增大,屈强比呈曲线增长趋势,在伸长率小于15%时增大较快,随后增长的梯度缓慢减小。主要原因如图8所述,316L奥氏体不锈钢在伸长率小于15%时具有优良的塑性,对加工硬化现象较敏感,屈服强度增大的倾向明显大于抗拉强度增大的倾向,当伸长率超过15%后,材料脆性增强,使得抵抗微量塑性变形的能力增强,受变形机制的限定,屈服强度增大趋势快速降低,因此会出现屈强比增大梯度减小的现象。
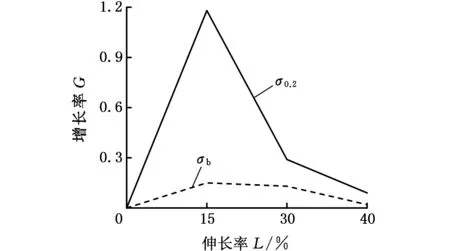
图8 不同伸长率下屈服强度与抗拉强度的增长率分布Fig.8 Distribution of growth rate and tensile strength under different stretching rates
2.2 维氏硬度测试结果讨论与分析
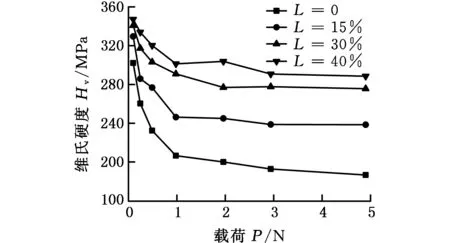
不同伸长率下,316L奥氏体不锈钢维氏硬度测试过程中,硬度随着压头压入载荷的变化情况如图9所示。可以看出,随着载荷的增大,三组试验得到的维氏硬度值均逐渐减小,且趋于稳定,即不同伸长率下316L奥氏体不锈钢均出现了不同程度的正ISE现象,随着伸长率的增大,ISE程度逐渐减小,且临界载荷越来越小。
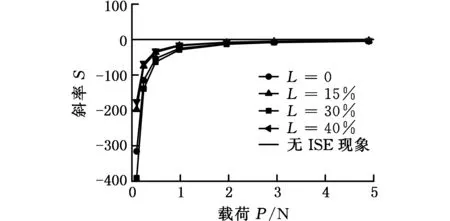
图9中各曲线斜率随压痕载荷的变化分布情况如图10所示。随着压痕载荷的增大,各伸长率下的Hv-P曲线斜率逐渐趋于“0”,即ISE现象趋于消失。压痕载荷在小于1 N时,材料越硬,曲线斜率越大,当超过1 N时,加工硬化作用对曲线斜率没有明显影响。从图10中可以初步看出,当载荷达到4.9 N时,斜率仍小于“0”,由此可以初步判断不同伸长率下的316L奥氏体不锈钢的真实硬度所对应的压痕载荷均大于4.9 N,在此载荷下测得的硬度值仍然会较大地受ISE现象的影响。
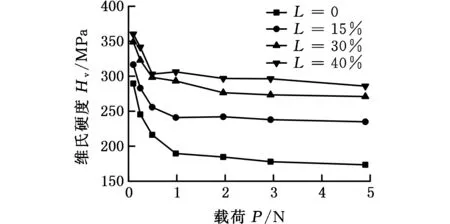
(a)第一组
(b)第二组
由于三组试验结果相差不大,为了便于分析,在对压痕尺寸效应分析时仍采用第一组试验结果作为分析基础。根据式(1)对试验得到的不同伸长率下Hv和载荷与压痕对角线长度平方的比值η=P/d2进行拟合,结果如图11所示。不同伸长率下316L奥氏体不锈钢的维氏硬度Hv与η成正比关系,且系数K均为0.19,R2为“1”,由此可以得出本试验所用维氏硬度仪的压头几何形状系数为0.19,而Vickers压头几何形状系数通常为0.189 1,可见试验过程中,压头几乎没有受磨损等因素的影响使得几何形状系数发生变化。
2.3 ISE理论模型拟合结果分析
目前,解释ISE现象常见的理论模型有PSR模型、MPSR模型和MFSL模型[13-14],本文通过这三种常见的理论模型对不同伸长率下的316L奥氏体不锈钢试验数据进行拟合分析。
2.3.1 PSR模型
PSR理论模型认为摩擦阻力对Vickers压痕对角线长度有影响,理论公式如下所示[15]:
P=a1d+a2d2
(3)
(4)
P/d=a1+a2d
(5)
式中,a1为与加载过程中压头与试样间摩擦阻力有关的系数,表征了ISE的程度;a2为与塑性变形有关的常数,用来表征材料的真实硬度HPSR,MPa。
(b)第二组
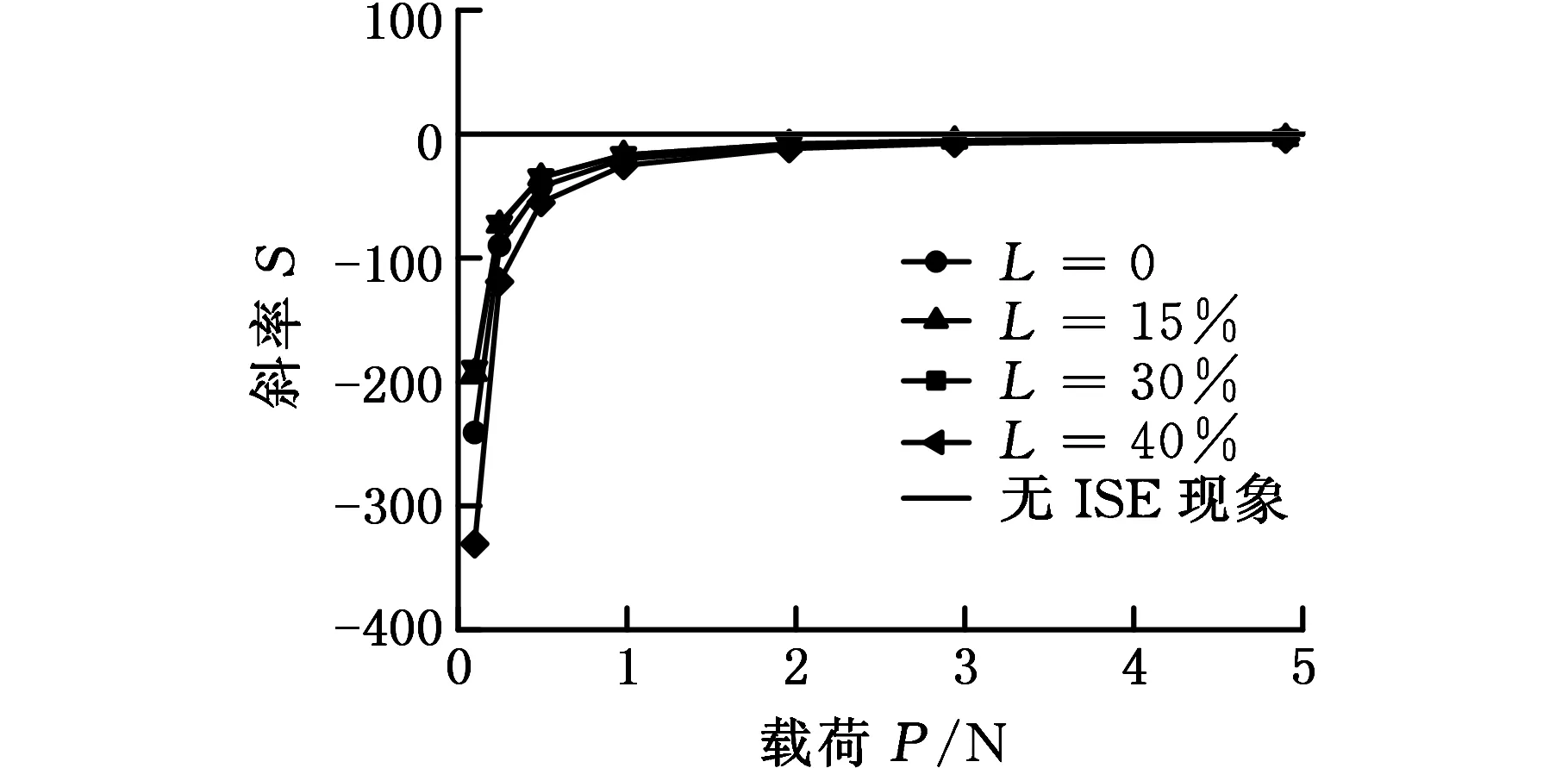
(c)第三组图10 不同伸长率下Hv-P曲线斜率随载荷P的分布Fig.10 Distribution of slope of Hv-Pcurve with load P under different stretching rates

图11 不同伸长率下维氏硬度随η=P/d2的变化分布情况Fig.11 Distribution of Vickers hardness withη=P/d2 under different stretching rates
根据PSR模型得到不同伸长率下316L奥氏体不锈钢ISE拟合曲线如图12所示,可以看出,各伸长率下载荷与压痕对角线平均长度比值τ=P/d和压痕对角线长度均值d成线性关系,且相关性都大于0.999,随着伸长率的增大,受加工硬化作用的影响,塑性变形所做的功减小,使得拟合直线斜率增大,即维氏硬度真实值逐渐增大。拉伸前后相比,a1有所减小,材料变硬,压头在压入试样的过程中摩擦阻力消耗的功略有减小,即ISE程度逐渐减轻。该理论模型下得到的结果与图9试验结果表现出的变化趋势相同,映证了该模型在解释ISE现象的准确性。
2.3.2 MPSR模型
MPSR模型是在PSR模型的基础上考虑了试样准备过程(研磨、抛光等)中表面产生的残余应力对ISE的影响,其压头载荷计算公式如下[16]:
P=a0+a1d+a2d2
(6)
(7)
式中,HMPSR为根据MPSR模型计算出来的真实硬度,MPa;a0为与测试样品的表面残余应力有关的常数。
通过MPSR理论模型得到不同伸长率下316L奥氏体不锈钢的ISE拟合曲线如图13所示,可以看出,随着伸长率的增大,曲线的曲率增大,a2逐渐增大,a0基本保持不变,由此可以得出,试样在准备过程中表面残留的残余应力很小,对ISE产生影响较小。主要是由于316L奥氏体不锈钢塑性较强、屈强比较小,在拉伸过程中,对加工硬化较为敏感,随着伸长率的增大,受加工硬化现象的影响,材料脆性增强,塑性降低,使得a2增大。由图7可得,随着伸长率增大,屈强比的增大幅度逐渐变缓,因此会使得a2增大的幅值减小。

图13 MPSR模型得到不同伸长率下316L奥氏体不锈钢的ISE拟合曲线 Fig.13 MPSR model to obtain ISE fitting curve of 316L austenitic stainless under different stretching rates
2.3.3 MFSL模型
针对压痕尺寸效应,MFSL模型考虑了测试过程会存在一个固有硬度和一个特征压痕对角线,即随着压痕对角线趋于无穷大,ISE会逐渐消失,其理论模型的计算公式如下[17]:
(8)
(9)
式中,Hm为材料的固有维氏硬度,MPa;d*为特征压痕对角线长度。

图14 MFSL模型得到不同伸长率下316L奥氏体不锈钢的ISE线性拟合 Fig14 MFSL model obtained ISE linear fitting of 316L austenitic stainless under different stretching rates
根据MFSL模型得到不同伸长率下316L奥氏体不锈钢的ISE拟合曲线如图14所示。随着材料塑性减弱,弹性性能增强,拟合直线的截距逐渐增大,即随着伸长率增大,固有硬度Hm增大,并且增大的趋势逐渐减小,理论模型求出的材料真实硬度随伸长率的变化趋势与真实情况相符。
表3是不同伸长率下,316L奥氏体不锈钢根据三种常见的ISE理论模型得到的真实硬度值。通过对比拟合相关性发现,MPSR模型拟合最为准确,因此可以得到0、15%、30%、40%伸长率下316L奥氏体不锈钢的真实硬度为159.16 MPa、228.07 MPa、259.72 MPa、282.54 MPa。

表3 不同ISE理论模型得到的不同伸长率下316L奥氏体不锈钢真实硬度
2.4 维氏硬度测试过程中ISE趋于消失的临界载荷确定
硬度是材料的特性,测试过程理论上属于准静态状态,但是实际中由于众多因素的影响会出现硬度随一定范围内的载荷变化而变化的现象,即所谓的“尺寸效应”。根据MPSR理论模型得到不同伸长率下316L奥氏体不锈钢真实硬度值与屈服强度的关系如图15所示,可以看出:通过MPSR理论模型得到的真实硬度与室温静态单轴拉伸试验得到的屈服强度基本成线性关系,与理论关系相符,由此证明了MPSR模型适用于冷加工过程中316L奥氏体不锈钢真实硬度计算,且结果较为准确。
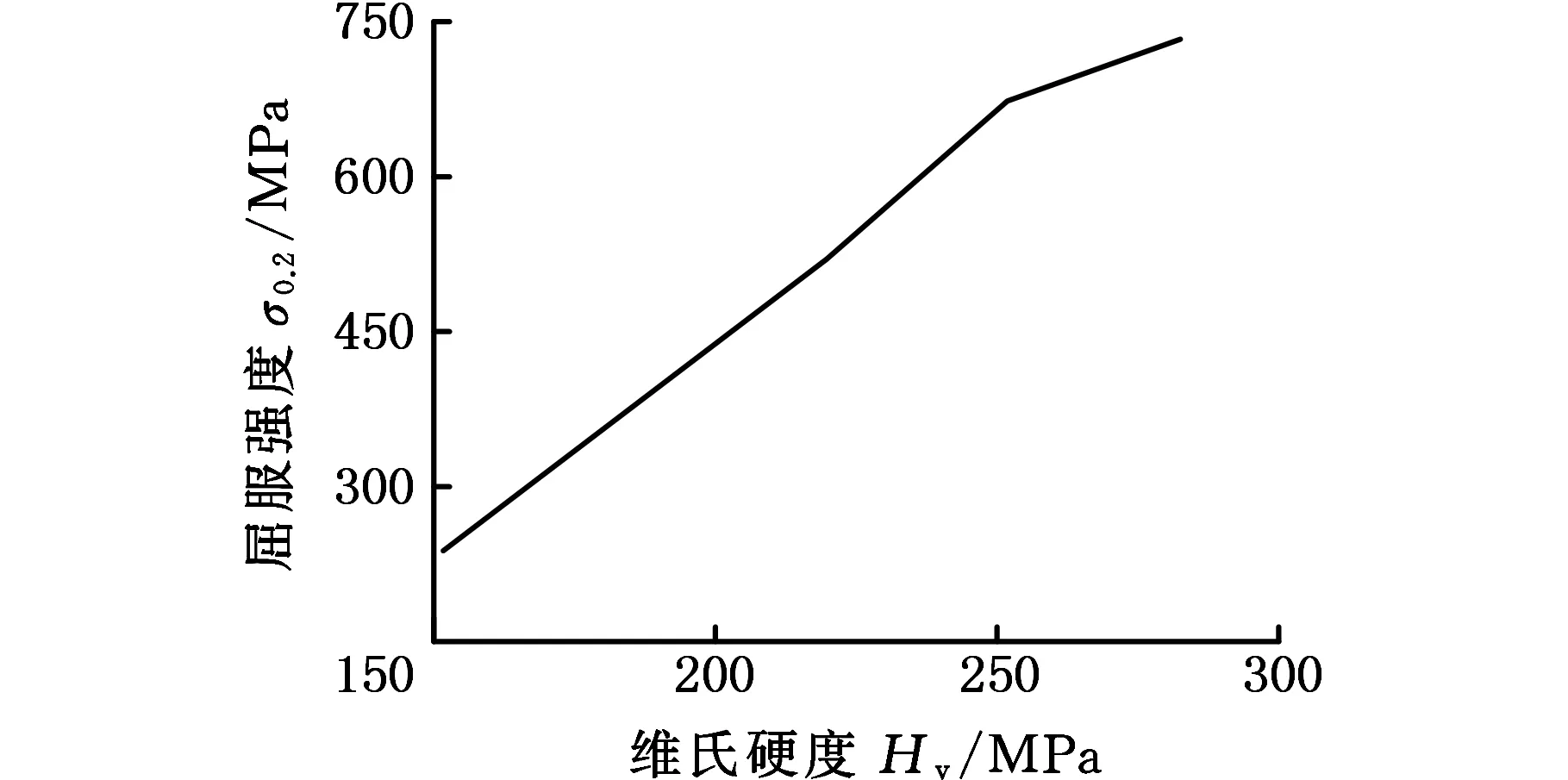
图15 屈服强度随维氏硬度的分布规律Fig.15 Distribution of yield strength withVickers hardness
不同材料出现尺寸效应的载荷范围是不相同的,本文研究对象是冷加工下的316L奥氏体不锈钢,根据图9、图10分析,通过压头载荷为9.8 N下得到的硬度值与MPSR理论模型计算结果进行对比,来验证此载荷是否在维氏硬度测试过程存在ISE现象,结果见表4。比较物理试验与MPSR理论模型得到的结果,当伸长率为零时误差最大,误差为4.17%,在允许误差(<5%)范围内,满足试验要求。其主要原因为316L奥氏体不锈钢属于弹塑性材料,伸长率为零时,塑性较强,而影响压痕尺寸效应的因素较多,包括压痕过程中的加工硬化、材料的混合弹塑性变形响应等材料性能变化等,结合图9发现,ISE程度随着伸长率的增大而逐渐减小,因此零伸长率下压痕尺寸效应最为严重,以9.8 N作为压头临界载荷得到的误差最大。

表4 不同伸长率下316L奥氏体不锈钢真实硬度与9.8 N下试验结果对比
3 结论
(1)通过对试验数据进行分析,得到冷加工过程中316L奥氏体不锈钢硬度测试过程中存在正压痕尺寸效应,且随着伸长率的增大,材料弹性性能增强,塑性减弱,压头在压入试样的过程中ISE各影响因素作用逐渐减小,使ISE程度逐渐减弱。
(2)借助PSR、MPSR、MSFL三种理论模型采用拟合的方法对0.098~4.9 N压头载荷范围内经过伸长率为0、15%、30%、40%单轴拉伸后的316L奥氏体不锈钢维氏硬度拟合结果进行分析,得出MPSR模型拟合度最高,并得到不同伸长率下316L奥氏体不锈钢的真实硬度值分别为159.16 MPa、228.07 MPa、259.72 MPa、282.54 MPa。
(3)利用屈服强度与硬度的关系验证了理论模型得到的材料真实硬度的准确性;随后对比了9.8 N压头载荷下测得的硬度值与理论模型计算出的真实硬度值,确定了利用HVS-1000Z型数字显微维氏硬度计在9.8 N压痕载荷下测量硬度几乎不存在ISE现象,得到的硬度值接近真实硬度,最大相差4.17%,在误差允许范围内。

