基于弹性摩擦模型的机器人免力矩传感器拖动示教方法

张 铁 洪景东 刘晓刚

(1.华南理工大学机械与汽车工程学院， 广州 510641; 2.桂林航天工业学院广西高校机器人与焊接重点实验室， 桂林 541004)

0 引言

目前，工业机器人一般采用示教器进行示教，通过编程的方法规划复杂的运动轨迹。为了缩短机器人示教时间并实现其定位和复杂轨迹的生成，可以采用手动引导机器人运动的方式，即拖动示教。拖动示教对于操作者来说，机器人的使用将变得更为方便，也可以轻松避开环境障碍。工业机器人的拖动示教通常使用力传感器来实现，然而传感器价格昂贵，在工业应用中推广存在困难，所以在免力矩传感器下实现拖动示教是优选方法。

基于机器人动力学模型和运动状态估计机器人关节所受的外力是实现拖动示教的一种常用方法，其中最简单的方法就是将模型计算得到的理论力矩和机器人返回的实际力矩进行求差得到外力的估计值[1]。文献[2-3]则采用基于机器人广义动量的干扰观测器，在没有使用关节加速度的情况下估计关节外力。文献[4]提出一种将动力学方程和递归最小二乘法相结合的外力估计方法，并与基于广义动量的估计方法进行比较。

免力矩传感器拖动示教的难点在于对关节摩擦的准确辨识，特别是关节在低速运动和静止状态下的关节摩擦力。当机器人处于高速运动时，由于关节摩擦的非线性较低，一般采用库伦+粘性摩擦的静态模型进行建模[5]。当关节处于低速状态时，摩擦环节的非线性变得突出，并对机器人的运动控制带来较大的影响[6-7]，其中包括由于摩擦形式的转变而导致的Stribeck效应[8]。库伦+粘性摩擦模型未考虑到Stribeck效应，且在角速度为零时存在不连续性，不适用于关节在低速和静止状态下的关节摩擦辨识。Leuven模型[9]和GMS模型[10-11]既考虑到Stribeck效应，又考虑了关节在静止状态下的预滑动位移和摩擦记忆等特性，是两个全面、精细的模型。但由于模型结构复杂且参数较多，具有很高的辨识难度。文献[12]采用一种弹性摩擦模型，该模型既能简单描述关节的动态摩擦现象，又极大地减少了需要辨识的模型参数。

除了关节摩擦的非线性外，关节内部的传动机构等也会给关节的运动引入更加复杂的摩擦[13]。关节内部的减速器机构、轴承、输入和输出轴等都存在摩擦，既有粘性摩擦，又存在干性摩擦，这使得关节在静止状态下的摩擦变得更加复杂，导致在拖动示教中，操作者往往需要更大的外力才能由静止状态起动关节[14]。为了解决关节在起动阶段的困难，文献[14]对弹性摩擦模型进行修改，采用变参数的方法调整拖动示教在运动和静止状态下的控制效果。文献[15]则通过在摩擦模型中引入振动，利用关节微小的高频振动减弱关节摩擦的非线性，但振动会对关节引入不稳定性，加快零件磨损。

本文通过在弹性摩擦模型中引入Stribeck摩擦项，提出一种结合弹性摩擦模型的起动规划方法，利用弹性模型的内在变量判断关节在静止状态下的起动意向，并通过短暂增加对摩擦力的估计值，以增加关节的驱动力矩，使关节可以轻松起动。

1 机器人拖动示教控制方案

为实现免力矩传感器下的拖动示教，需根据机器人的动力学模型和运动状态，估计操作者施加在机器人上的关节外力，并将估计的外力转换为机器人的运动指令。本节采用基于广义动量的外力估计[2-3]方法，在缺少关节角加速度信息下进行外力估计。使用导纳控制方案生成运动指令，并推导了离散状态下的关节目标位置的更新方程。

1.1 基于广义动量的外力估计

采用基于广义动量的外力估计方法，利用机器人的动力学模型和运动状态，对操作者施加在机器人上的外力进行估计。机器人动力学模型为[4]

(1)

式中q——关节转角向量

M(q)——惯量矩阵

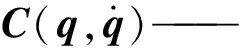
G(q)——重力项τf——摩擦项

τ——电机输出力矩

τext——外力矩向量

动力学模型满足

(2)

通过定义机器人的广义动量

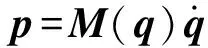
(3)

结合式(1)、(2)，对式(3)进行求导可得

(4)

建立对p的观测量，其定义为

(5)

其中

r=K(p-)

(6)

式中r——残差量K——比例系数

其中上标代表相应变量的观测值和估计值。由于关节摩擦力的辨识较为重要和困难，本文采用基于弹性摩擦模型的方法得到f，具体将在第3节进行讨论，而其他动力项的估计值可参照文献[5]。假设估计量与实际值相比没有误差，结合式(4)、(5)对式(6)进行求导可得

(7)

将式(7)进行拉普拉斯变换可得

(8)

可见R以一阶系统的形式对Γext进行跟踪，在稳态时，有R(0)=Γext(0)，因此可以使用r作为外力矩τext的估计值，即

ext=r

(9)

1.2 机器人导纳控制方法

阻抗控制(Impedance control)和导纳控制(Admittance control)被广泛应用于机器人的力控制算法中。在应用中，阻抗控制通过调整电机力矩响应实现阻抗功能，而导纳控制则是基于位置规划实现[16]。相比于阻抗控制，导纳控制稳定性高，但灵敏度较低[17]。本节通过导纳控制，将关节的估计外力转换为关节的运动目标指令，并推导离散空间下的更新方程。

在机器人关节空间，完整的阻抗控制可表示为

(10)

式中Kd——系统刚度

Dd——系统阻尼

Md——系统质量

qd——机器人运动的目标关节角

qr——规划的参考轨迹

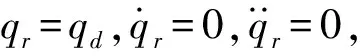
(11)

将机器人的导纳算法进行离散化，且满足前提条件

(12)

式中Ts——时间周期

由式(12)可以得到目标轨迹在离散系统下的更新方程为

(13)

将得到的目标跟踪轨迹qd发送到机器人的伺服驱动器，驱动机器人关节跟踪目标轨迹，由此实现免力矩传感器的拖动示教。

2 基于弹性摩擦模型的关节摩擦估计

在第1节的外力估计方法中，外力估计的精度很大程度取决于机器人动力学模型和参数的准确性，其中对关节摩擦力的辨识尤为重要。当关节处于低速状态时，由于Stribeck效应的影响，关节的摩擦力会显著上升，这种效应需要在摩擦模型中得到体现。而当关节处于静止状态时，关节的微小转动便可产生较大的摩擦力，即静态摩擦力，同时伴随有预滑动滞后等现象[19]。为了能够辨识出关节在静止状态下的摩擦力，本节采用弹性摩擦模型对关节摩擦力进行估计，同时在摩擦模型中引入Stribeck摩擦项，以提高模型在低速运动下的摩擦估计精度。

弹性摩擦模型的示意图如图1所示。弹性摩擦模型定义了一个弹性摩擦单元，该单元与关节臂存在弹性连接关系，其刚度为Kc。弹性摩擦单元位置为qc，关节臂位置为q，弹性摩擦单元产生的干性摩擦力为τfc。由于弹性摩擦单元没有质量，所以在力学上满足

τfc=(q-qc)Kc

(14)

干性摩擦力τfc具有上下限，定义为τfc∈[-Fc,Fc]，其中Fc相当于关节在转动状态下的库伦摩擦力。当关节处于运动状态时，τfc恒为Fc。同理，q-qc也相应地有上下限的约束。

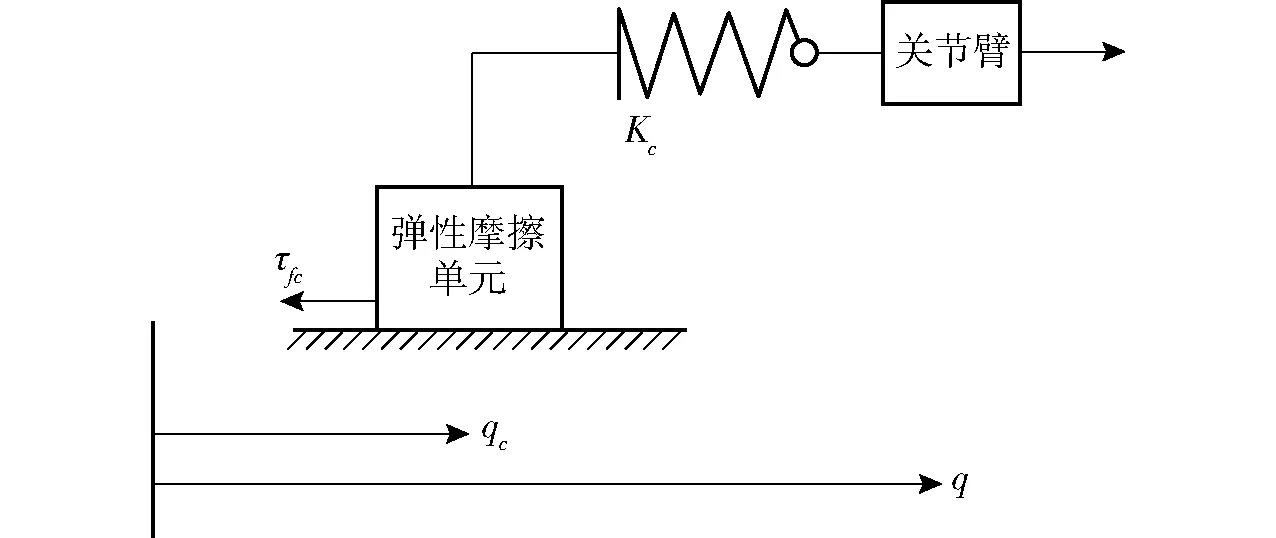
图1 弹性摩擦模型示意图Fig.1 Schematic of elastic friction model

弹性摩擦模型的摩擦单元在离散状态下的更新方程为[12]

(15)

其中

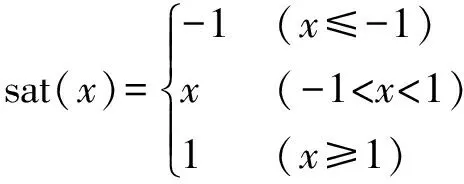
(16)

式中α定义了一个收敛速度，表示弹性摩擦元件会自行向关节位置靠拢。Fc、Kc和α共同定义了关节的弹性摩擦模型，简单地描述了关节的摩擦特性。

通过差分运算可以得到弹性摩擦单元的运动速度为

(17)

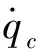
(18)

式中Fcc——不考虑Stribeck效应时的库伦摩擦力

Fcs——关节存在的最大静摩擦力

Vs——Stribeck速度

γ——经验参数，用于控制曲线的形状

式(18)描述了关节的库伦摩擦力，而对于关节的粘性摩擦力τfs描述为

(19)

式中fs——粘性摩擦系数

由于关节摩擦力等于干性摩擦力和粘性摩擦力之和，故有

F=τfc+τfs

(20)

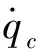
3 关节摩擦估计的起动规划

弹性摩擦模型可以对关节在静止状态下的摩擦力进行简单估计，但仍无法描述其他更复杂的非线性特性，如关节在预滑动位移阶段的滞回现象等，同时由于关节传动机构间的挤压和摩擦等会引入更加复杂的摩擦力，使得关节在静止状态下的拖动示教变得异常困难[14-15]，操作者往往需要施以更大的外力才能使关节成功脱离静止状态。

为了实现机器人的轻松拖动，本节对关节的起动过程进行规划。利用弹性摩擦模型的内部变量，判断关节在静止阶段是否有起动的意向。当检测到关节的起动意向时，短暂并大幅地增加摩擦估计值。起动规划算法如图2所示。

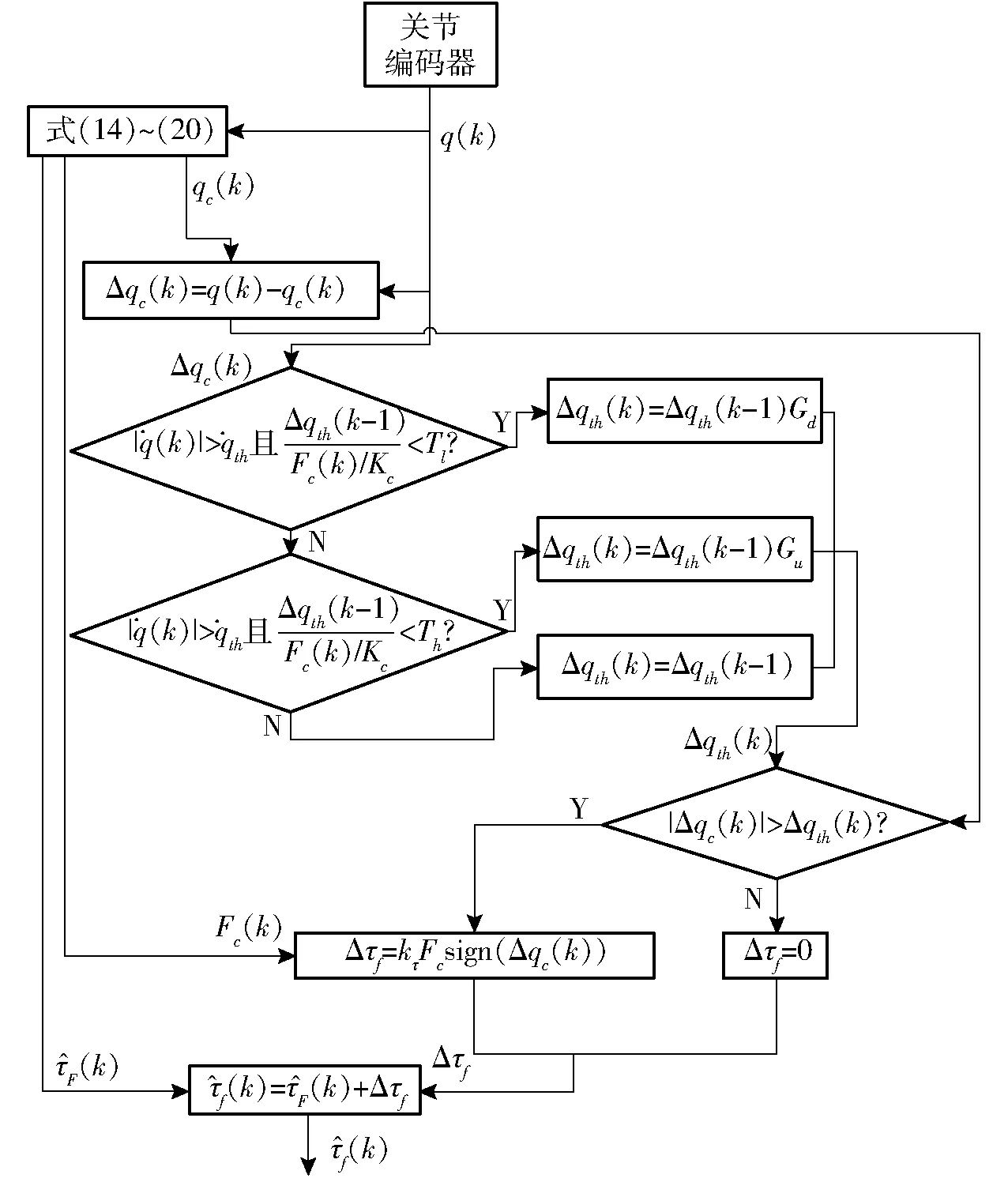
图2 机器人起动规划算法Fig.2 Robotic starting planning scheme

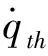
起动规划算法基本流程为：①根据式(14)～(20)计算弹性摩擦模型的摩擦估计值，定义为F。返回弹性模型中摩擦单元的位置qc，并与关节实际位置q做差得到Δqc。②更新Δqth，当关节处于静止状态，即时，Δqth不断下降直到其下限值否则Δqth上升直到其上限值③比较Δqth和|Δqc|的值，当|Δqc|>Δqth时表示关节处于起动阶段，此时摩擦估计补偿值Δτf为kτFcsign(Δqc(k))，否则为零。④将弹性摩擦估计值F和摩擦估计补偿值Δτf求和得到规划后的关节摩擦估计值f，由此完成对关节摩擦力的估计。

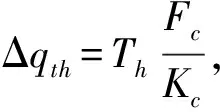
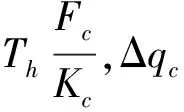
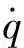
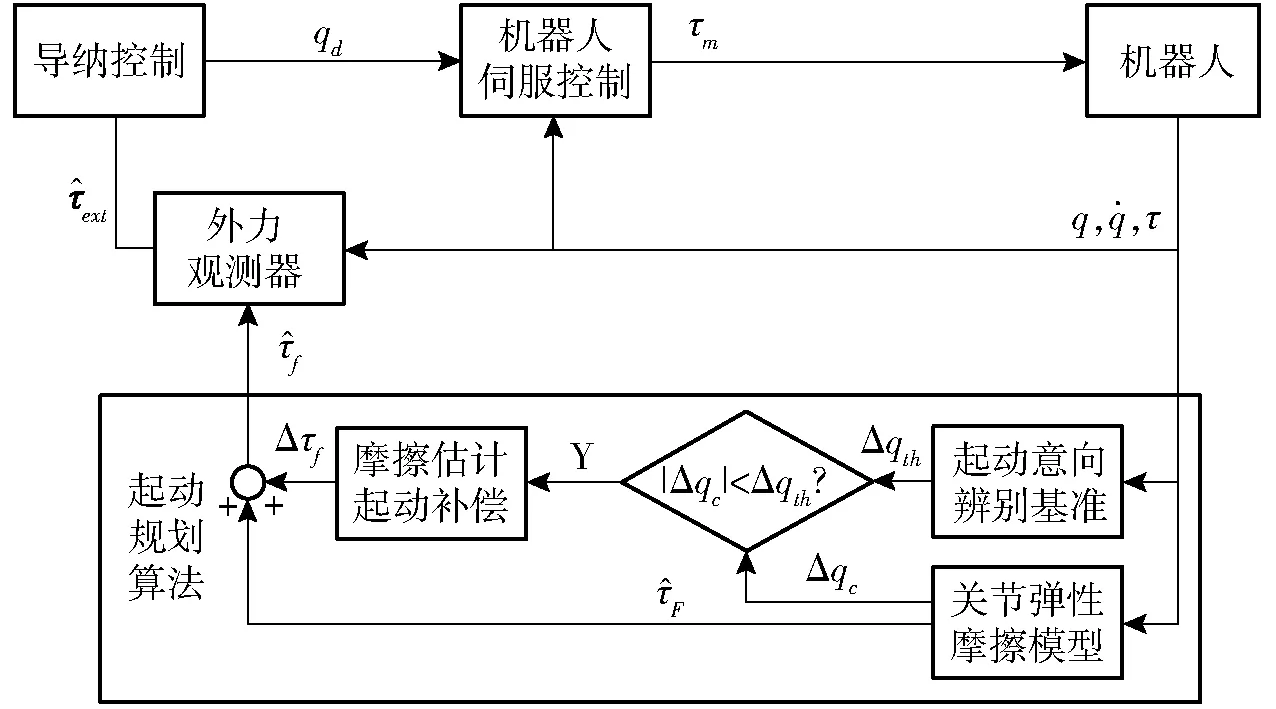
图3 机器人拖动示教控制方案Fig.3 Robotic dragging teaching control scheme

图4 机器人实验平台Fig.4 Robotic experimental platform

4 免力矩传感器的机器人拖动示教实验

4.1 机器人实验平台

使用广州数控RB08型机器人进行拖动示教实验，系统结构如图4所示。使用装载实时控制系统的工控机作为上位机，并采用EtherCat协议进行通信。驱动器的位置参考由上位机计算并发送，电机关节的力矩测量值采用电流控制器的参考值。控制系统以1 000 Hz的频率进行通讯和控制，即控制周期Ts为1 ms。由机器人的前3个关节进行拖动示教实验。

4.2 机器人动力学模型

4.2.1关节Stribeck摩擦参数辨识

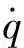
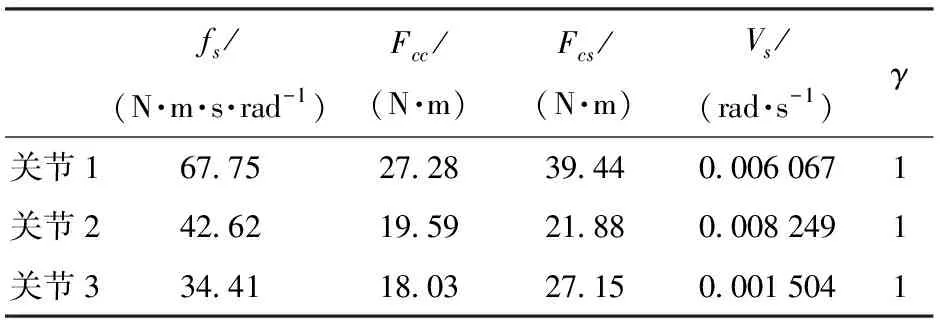
表1 Stribeck摩擦模型参数Tab.1 Parameters of Stribeck friction model

4.2.2其他动力学参数辨识

机器人的其他动力项参数，如重力、离心力和科氏力等，由于存在耦合现象，只能得到一组最少参数集，且动力学方程一般写成线性结构[5]

(21)

式中Γ——关节计算力矩

Hb——与机器人运动状态相关的矩阵

β——动力学最少参数集

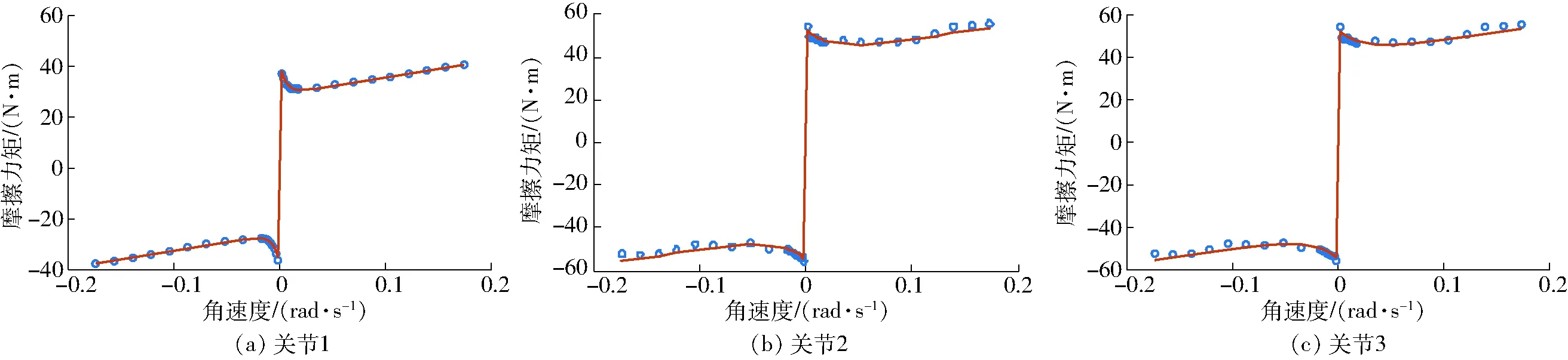
图5 Stribeck模型拟合曲线Fig.5 Fitting curves of Stribeck model

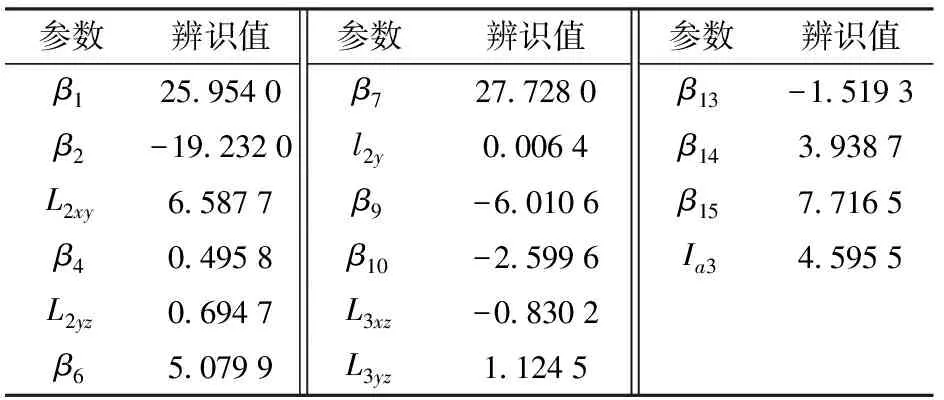
表2 非摩擦项动力学参数Tab.2 Dynamics parameter set of non-friction term kg·m2

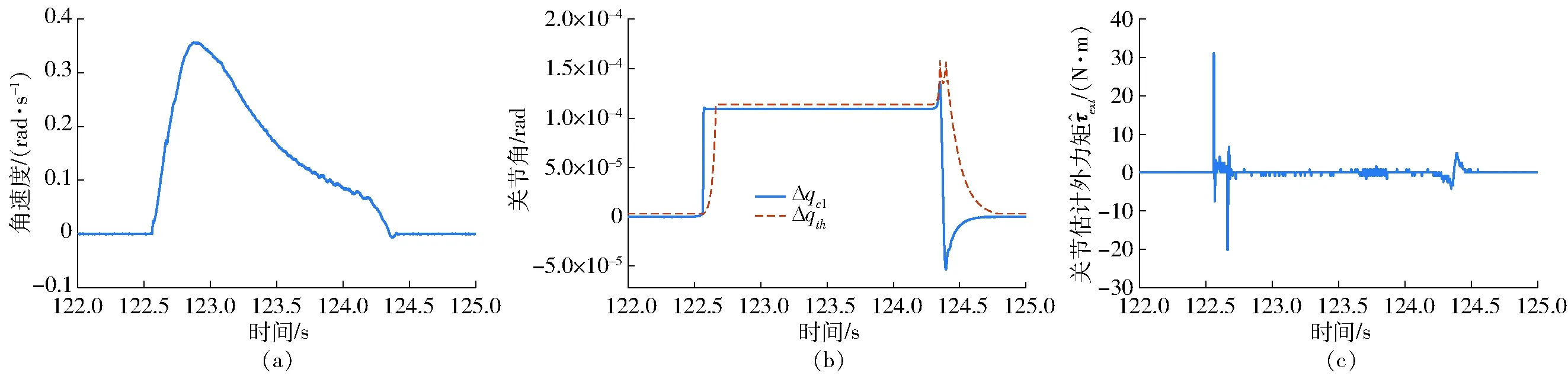
图6 关节1拖动实验(采用起动规划)Fig.6 Drag experiment of joint 1 (using starting planning)

通过辨识到的机器人参数和机器人运动状态，便可计算出机器人各动力项的估计值，如、f等，通过基于广义动量的外力估计方法，根据式(1)～(9)便可求得外力估计值ext，其中式(7)中参数K的值在3个关节的实验中都设为600。

4.2.3机器人拖动实验

使用弹性摩擦模型和起动规划算法进行机器人的关节起动实验，机器人前3个关节的参数设置如表3所示。为提高运动的稳定性，Kc的设定值都小于实测的摩擦刚度，这使得当关节在低速运动时容易自行减速到静止状态。按照起动规划算法，前3个关节的起动拖动实验如图6～8所示。只采用式(20)的输出F作为关节摩擦的估计结果时，其实验结果如图9～11所示。对比相同关节在两次实验中的结果，关节在起动的瞬间，使用规划算法产生了较大的估计力矩ext。图6c在起动过程中产生了31.09 N·m的估计力矩，而图9c最高为2.521 N·m。图8c起动阶段产生最大力矩为26.05 N·m，而图11c为5.881 N·m。在使用起动规划算法时，关节的Δqc在短时间内便可快速上升到最大值。图6b中Δqc从0上升到最大值需要的时间为47 ms，而在图9b则需要161 ms，相比减少70.81%。图8b中，关节起动所需时间为66 ms，而图11b则需要263 ms，相比减少74.90%。

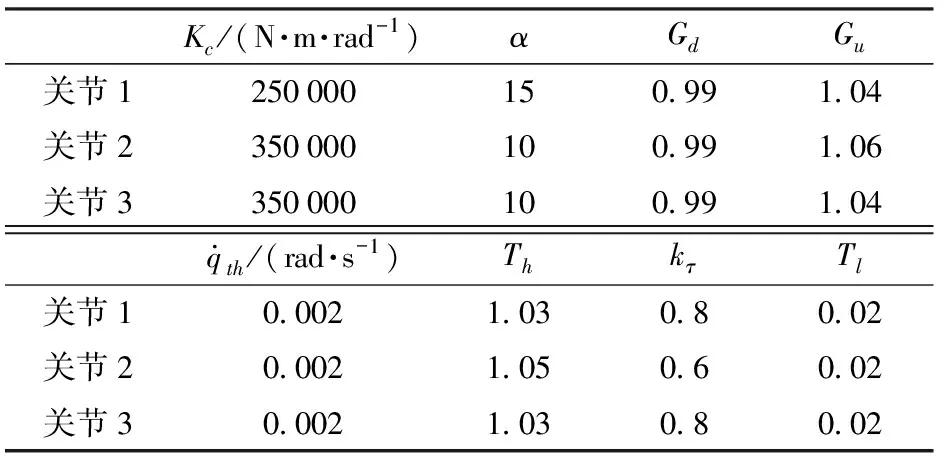
表3 起动规划算法参数Tab.3 Parameter of starting planning

图7 关节2拖动实验(采用起动规划)Fig.7 Drag experiment of joint 2 (using starting planning)

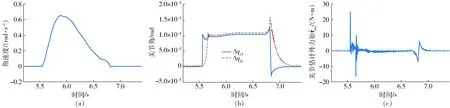
图8 关节3拖动实验(采用起动规划)Fig.8 Drag experiment of joint 3 (using starting planning)

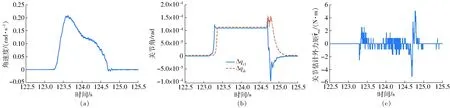
图9 关节1拖动实验(未采用起动规划)Fig.9 Drag experiment of joint 1 (without using starting planning)

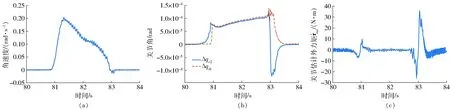
图10 关节2拖动实验(未采用起动规划)Fig.10 Drag experiment of joint 2 (without using starting planning)

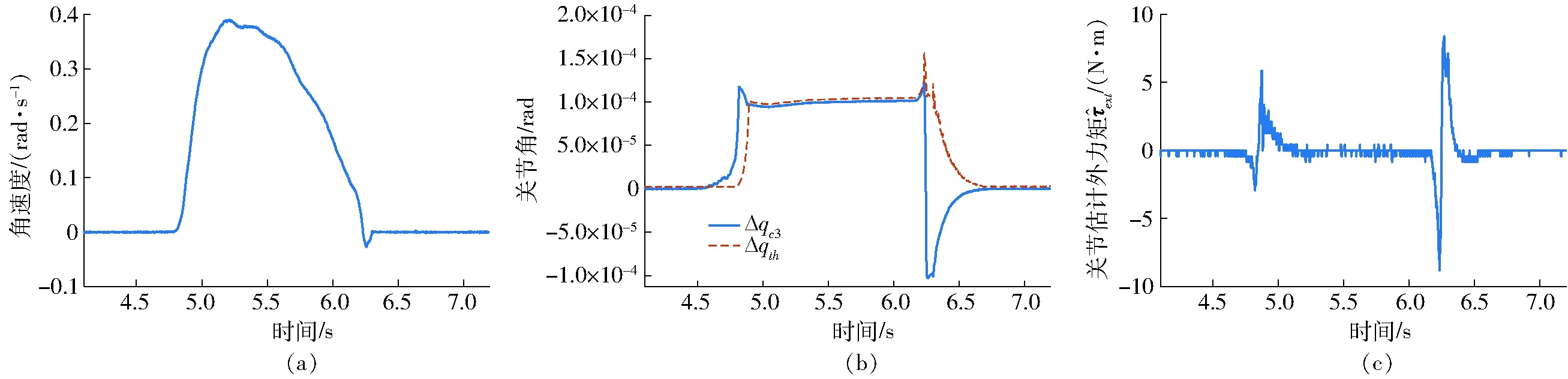
图11 关节3拖动实验(未采用起动规划)Fig.11 Drag experiment of joint 3 (without using starting planning)

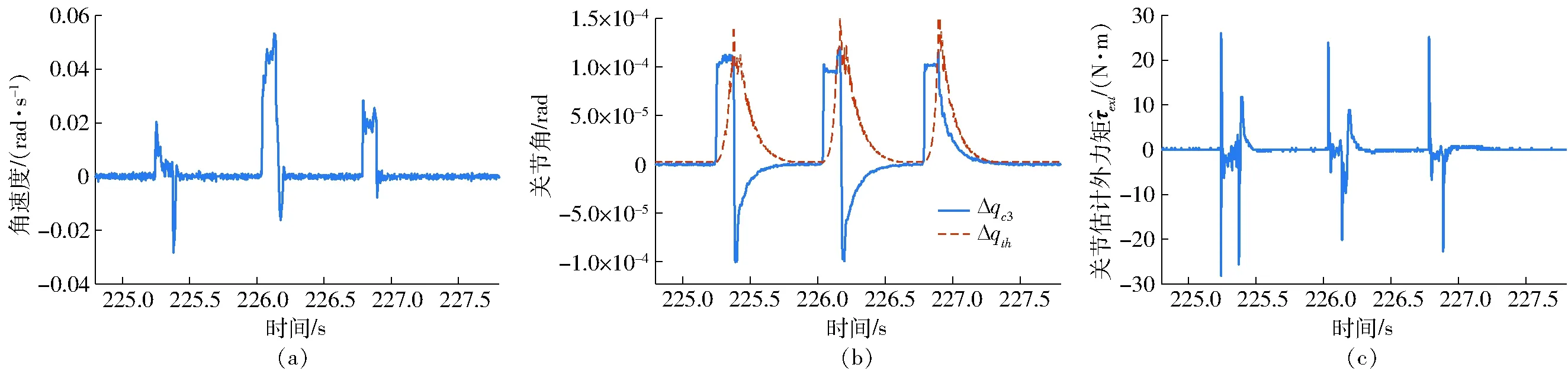
图12 关节3的抗干扰实验Fig.12 Anti-interference experiment of joint 3

由于本文是在机器人关节空间上实施导纳控制，且施力点在最后1个关节末端上，这使得操作者需要通过关节3间接对关节2进行施力拖动，导致关节2拖动效果并没有关节1和关节3好。基于机器人笛卡尔空间进行导纳控制的示教方法可以有效解决这个问题。

起动规划算法生成的摩擦估计补偿是十分短暂的，需要操作者在关节起动阶段不断施加外力才能使得关节进入较高速度的运动状态，否则关节容易减速并回到静止状态。这个特性使得关节在起动阶段具有一定的抗干扰能力。通过对机器人关节3进行连续3次轻敲，实验结果如图12所示。可以发现，虽然在关节起动阶段产生了大幅的外力估计值，但由于没有持续的外力，关节最终收敛回静止状态。

5 结论

(1)基于广义动量的外力估计和导纳控制算法，在免力矩传感器的条件下实现对工业机器人的拖动示教。使用弹性摩擦模型对关节的摩擦值进行估计，通过在弹性摩擦模型中引入Stribeck摩擦项，提高关节在低速时的摩擦估计精度，实现关节在低速和静止状态下的关节摩擦估计。

(2)提出了一种机器人起动规划方法，结合弹性摩擦模型的内在变量，对关节的起动意向进行判断并增加关节的摩擦估计值，实现关节的轻松起动。起动规划算法不会对机器人的其他运动阶段造成影响。

(3)实验表明，采用起动规划可以有效增加关节的外力估计值，规划后外力估计力矩可达26 N·m以上。使用规划算法可以缩短关节起动的时间，其中关节1减少70.81%，关节3减少74.90%。同时，机器人的拖动示教方案使得关节在起动阶段具有一定的抗干扰能力。