利用探针法研究二次电子发射过程中介质材料的表面电位

殷明,翁明,刘婉,王芳,曹猛

(西安交通大学电子物理与器件教育部重点实验室,710049,西安)

自从1899年Campbell发现了二次电子发射现象[1]之后,人们一直在对二次电子的发射特性和机理进行研究[2-4],并将其应用到各个领域。一方面,在电子倍增管、扫描电子显微镜等器件中均需要利用二次电子发射[5-6];另一方面,在微波器件、粒子加速器等领域中则需要避免二次电子发射,以防止微放电效应的发生[7-9]。

目前,虽然对于金属材料二次电子发射的研究已经有了长足的进步[10-11],但是对介质材料二次电子发射过程的研究尚不完善。因此,为了实现对介质材料二次电子发射特性的研究,首先需要了解介质材料带电后的表面电位变化情况。开尔文探头(Kelvin probe)作为一种非接触无损振荡电容装置,是目前测量导体材料的功函数或半导体、绝缘体表面电位最为常用的方法,并且已经在研究介质材料二次电子发射方面得到了一定程度的应用[12-14]。但是,在测量介质材料的二次电子发射特性及其表面电位时,由于Kelvin探头的尺寸较大,会阻挡电子束照射样品。若电子束先照射样品,然后再将Kelvin探头从照射区外移动至照射区,这不仅无法实现原位和在线测量,而且增加了真空设备的复杂性,使研究成本上升。

本文基于课题组的实验平台[15-17],将二次电子发射系数(SEY)的测量与介质表面电位的测量联系在一起,提出了一种简便的能实现原位和在线测量介质表面电位的探针法,并对其原理和合理性进行了仿真与实验验证。最后,基于探针法对PMMA材料的表面电位及其影响因素进行了研究。

1 探针法原理的仿真与验证

Computer Simulation Technology公司的CST软件是面向3D电磁、电路、温度和结构应力设计工程师的一款全面、精确、集成度极高的专业仿真软件包,其中的粒子工作室含有固定能量、空间电荷限制流、温度限制流、场致发射、二次电子发射和爆炸发射等多种粒子发射模型,主要应用于电真空器件、高功率微波管、粒子加速器、聚焦线圈、磁束缚、等离子体等自由带电粒子与电磁场自洽相互作用下相对论及非相对论运动的仿真分析[18-19]。本文利用CST软件,对探针法的原理和正确性进行了仿真。

1.1 实验装置与软件建模

实验装置是在课题组原有的介质材料二次电子发射特性测试平台[15]的基础上加以改进得到的,如图1所示。真空室内的真空度为7×10-4Pa,真空室内置有电子枪、金属桶形收集极、平板金属样品托、样品以及金属探针。利用电池供电的LM317集成电路模块作为可调电压源,可为收集筒、探针和样品托分别加上不同的偏压Vc、Vp、Vs,并由万用表Fluke 117C测得。电子枪自上而下发射束流大小为IPE的电子束,穿过探针并轰击到样品,由样品出射的二次电子被收集筒收集。在此期间,流过收集桶、探针和样品的电流Ic、Ip、Is经过50 kΩ的取样电阻后,由示波器Hantek DSO3104相应的通道CHc、CHp和CHs检测出,用于计算SEY。

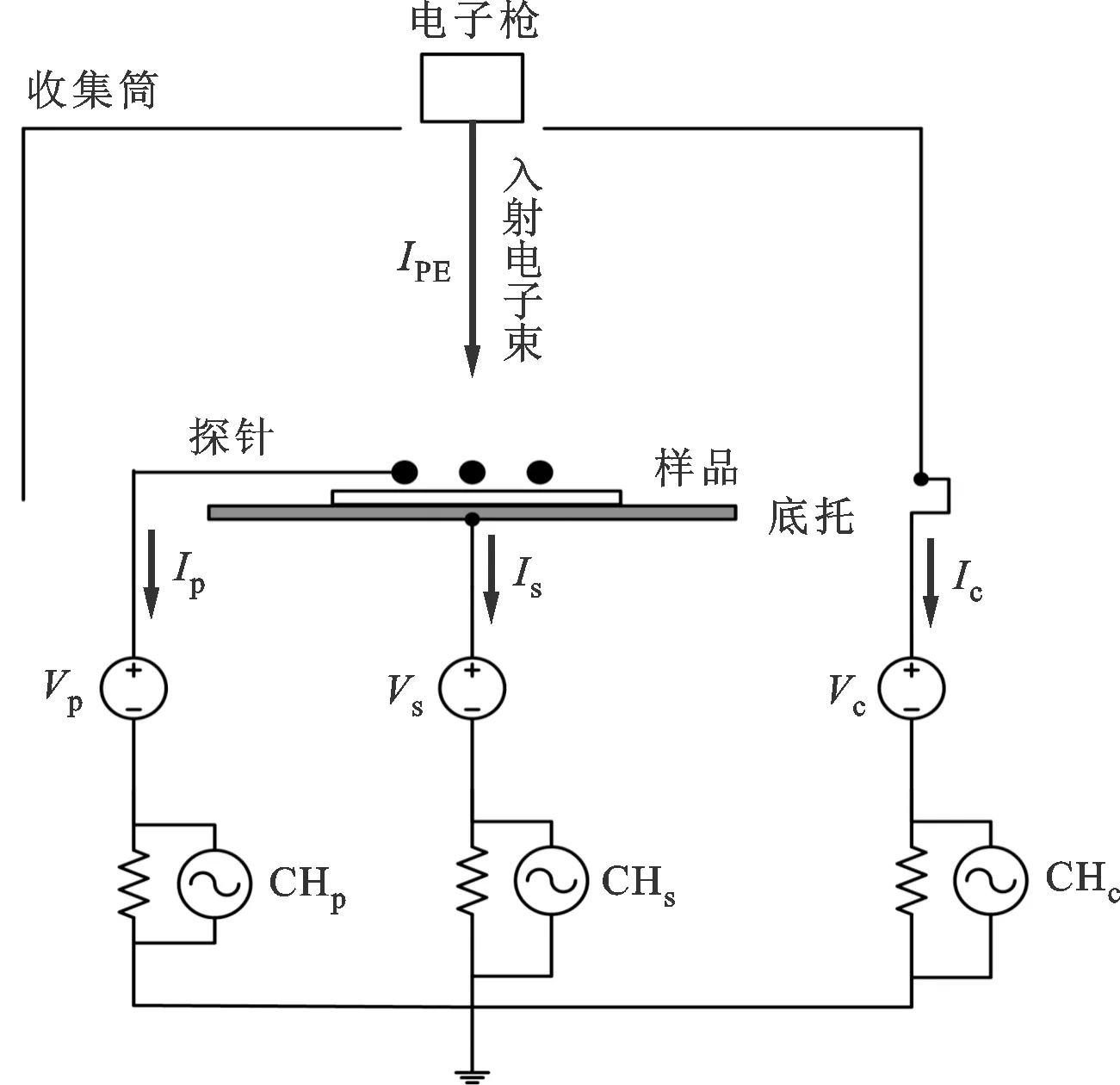
图1 实验装置图

根据实验装置,利用CST软件中的几何模型以及各种布尔操作进行了建模。在实际仿真中发现,单根探针对二次电子出射的影响较小,实验结果不够明显,因此在电子束束斑直径为14 mm时,选用直径为1 mm、轴线在样品上方0.9 mm处、相互间距为5.9 mm的3根圆柱体为3根探针,以取得较好的效果。在材质方面,仿照实验装置中将收集筒、探针、样品托的材质均设置成铜,并且忽略它们的二次电子发射。而为了给样品设置想要的表面电位Us,将其定义为导体材料,在这种情况下设定的样品托的偏压Vs即为样品的表面电位Us,设置二次电子发射特性为Vaughan模式,设置电子枪的发射模式为直流,电子束流大小IPE设置为10-6A。

当改变探针上所加的偏压Vp,可以研究Vp对探针附近电场的影响,并跟踪二次电子的运动情况,最终研究SEY与Vp的关系。

1.2 探针附近的电位分布

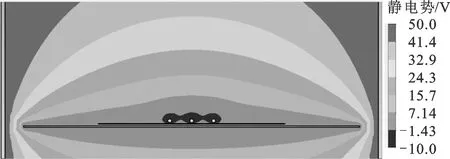
(a)Vp=-10 V

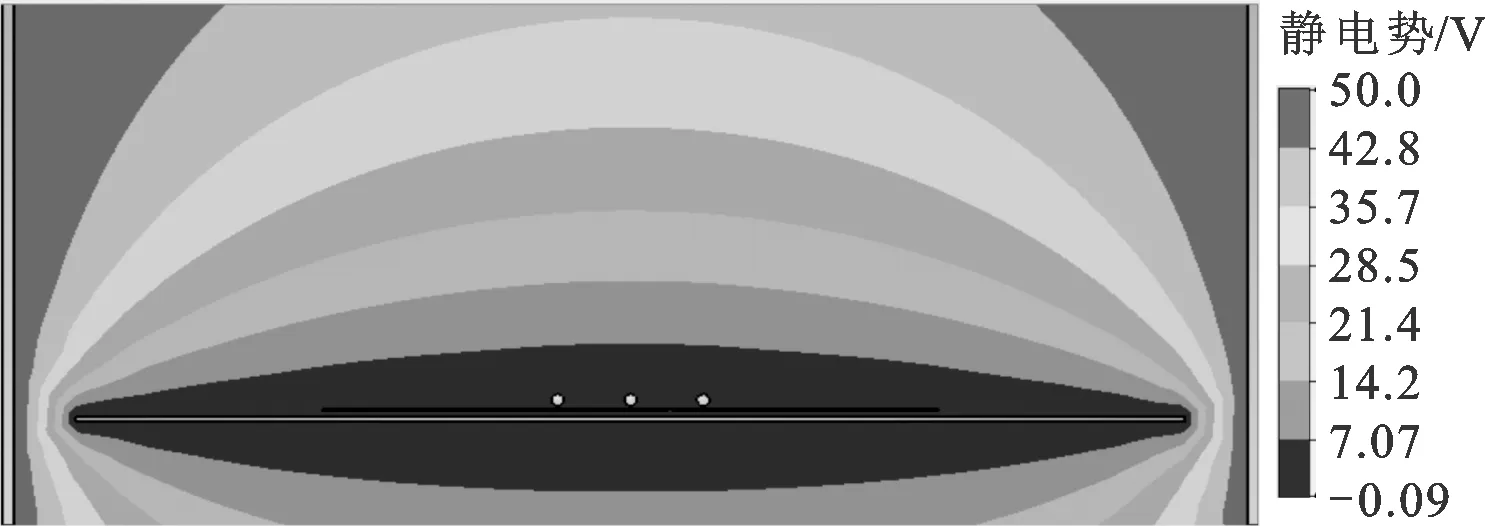
(b)Vp=0 V

(c)Vp=10 V图2 探针附近的电位分布图

当Us为0 V,Vp分别为-10、0、10 V时,CST仿真得到的探针附近电位分布情况如图2所示。由图2可知:当Vp为-10 V时,探针附近的电位低于Us,该处出射的部分二次电子会被压回样品表面,最终造成SEY减小;当Vp为0、10 V时,探针附近的电位分布有利于该处二次电子的出射,由样品出射的全部二次电子均可被收集筒收集到。因此,当Vp等于或高于Us时,对于SEY没有显著影响,而当Vp低于Us时,会抑制二次电子的出射,使得SEY降低。

1.3 样品表面电位测量的仿真

在进行了探针附近电位分布对二次电子出射影响的定性分析后,进一步利用CST软件的功能,定量仿真电子束入射、电子束轰击样品、由样品表面出射二次电子、二次电子受探针附近电场的影响以及二次电子最终被收集桶收集这一系列过程。

首先,在CST粒子工作室中设定好样品表面的二次电子发射特性,当电子轰击到样品表面时,CST软件会根据内置的理论模型发射出对应的二次电子,而这些出射的二次电子又会根据空间电位分布有着不同的运动方式,最终一部分被收集筒收集到。通过监测最终收集筒上接收到的所有碰撞电流Ic,即可计算出仿真实验中的二次电子发射系数

(1)

由于探针的遮挡效应,所以本文中研究的SEY均为样品与探针混合的二次电子发射系数。在设定Us为-5、0、5 V时,通过改变Vp来观察δ1的变化,结果如图3所示。由图3可知,δ1随Vp变化的曲线与前面定性分析的相同,当Vp小于Us时,δ1明显降低,而当Vp大于等于样品表面电位时,δ1基本保持不变,所以选取Vp相比Us较高时的δ1,求均值后得到恒定值(称为拐点)。图3中δ1与Vp关系中的拐点位置由垂直虚线标出,它们基本上与样品预先设定的Us相同,这说明δ1与Vp关系中的拐点对应的Vp实际上就是待测的样品表面电位。

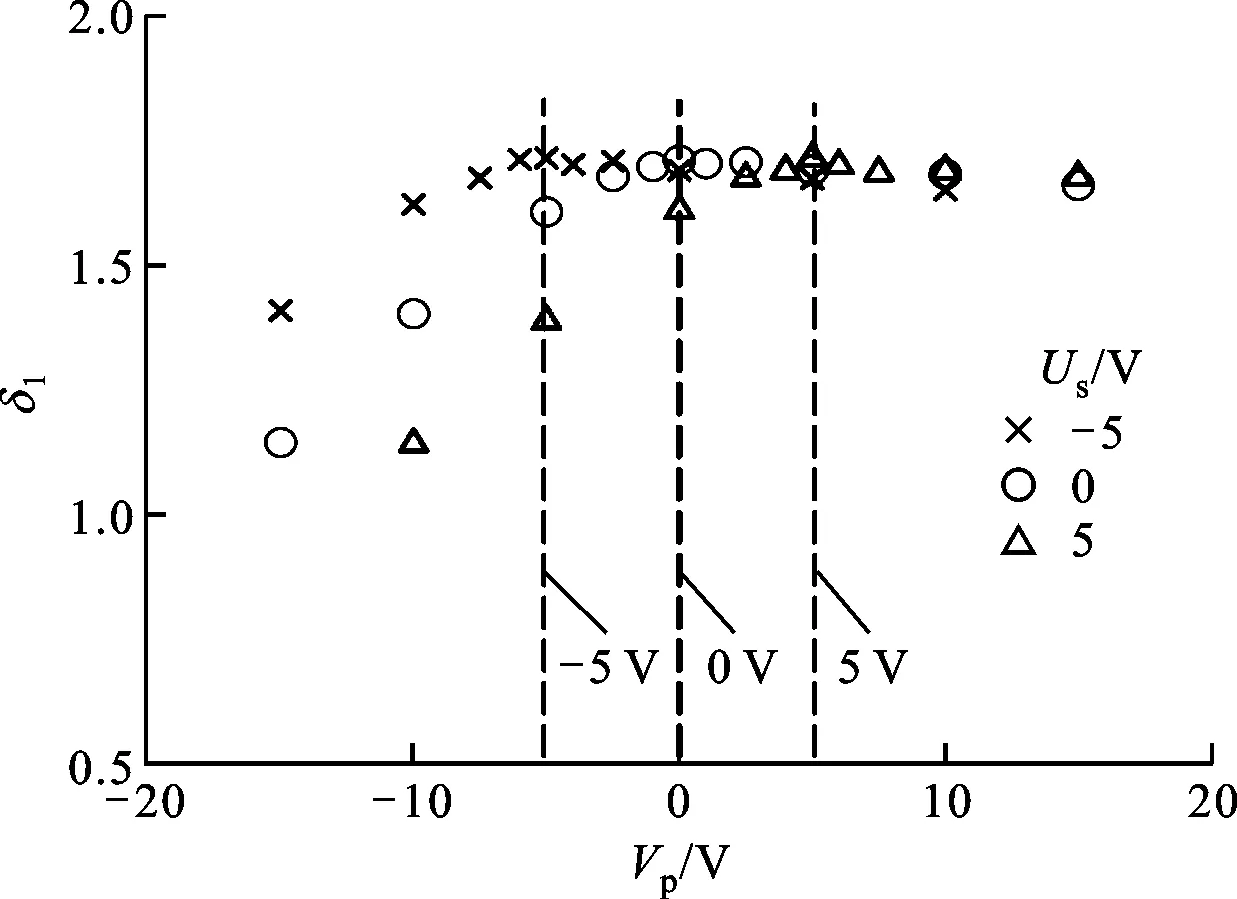
图3 仿真中不同Us下δ1与Vp的关系

1.4 探针法的实验验证

本文用图1所示实验装置,对探针比较法测量样品表面电位的原理进行了验证。在实验中,将探针与样品分开约0.4 mm的距离,并设定入射电子能量为300 eV,收集桶电压为40 V,铜样品的表面电位Us由样品托的偏压Vs决定,分别为-5、0、5 V。流过收集桶、探针以及样品的电流Ic、Ip和Is分别由示波器测出,验证实验中的二次电子发射系数为

(2)

测量结果如图4所示,可知δ2与Vp关系中的拐点均在对应的Us附近。仿真与实验所测得的Us均与实际给定的表面电位相同,这说明利用探针法测量表面电位是合理可行的。

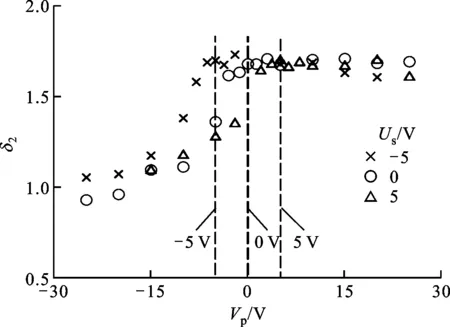
图4 铜样品在不同Us下δ2与Vp的关系

2 PMMA样品表面电位及影响因素

本文将探针法应用于介质材料表面电位的测量,被测样品为厚度1 mm的PMMA材料,保持样品托的偏压Vs为0。在图1所示装置中,若样品为介质材料,那么电子束照射样品后,其表面将积累电荷。当入射电子能量位于样品SEY与一次电子能量关系曲线中第1、2交叉点之间时,样品SEY大于1,意味着样品表面将建立起正的表面电位,这一电位将会抑制样品表面出射的二次电子,使SEY值下降,直至SEY值等于1,并最终使样品的表面电位Us恒定,这说明样品的Us与入射电子能量EPE、样品本身的二次电子发射特性等因素有关。

2.1 PMMA表面电位的测量

用探针法测量样品Us的基础是对SEY的测量,而对于介质材料SEY的测量,采用了课题组以往的测量思路[15-17],SEY的测量分2步完成。第1步,对样品进行中和,中和的目的是让样品带电,并达到稳定状态,使其具有相应的Us,而且保证每次测量后,样品的Us能够保持固定,不受测量过程的影响,为了让样品带电均匀,本文在探针上方5 mm处放置了一个由金属网构造的平面栅网,尽可能保证栅网和样品之间有一个均匀电场,以使得最终样品表面的电位分布均匀;中和时保持收集桶偏压不变,为40 V,并给定一个栅网偏压Vg,让电子枪输出连续脉冲照射样品,同时探针处于悬浮状态。第2步,当中和完成之后,保持收集桶与栅网相连并设偏压为40 V,然后设定一个Vp,让电子枪输出一个单脉冲,照射样品,同时用示波器记录下相应Ic、Ip、Is的电流波形,并按照式(3)计算测量实验中的二次电子发射系数δ3。这两步交叉进行,直至获得完整的δ3和Vp关系曲线。由于平面栅网的引入,式(2)将变化为式(3),其中t是由栅网的几何结构决定的电子透过率,在本文实验中t约为0.9。同时,为了降低在测量过程中样品的带电造成δ3下降而带来的测量误差,采用脉冲电流的峰值Icmax、Ipmax、Ismax计算δ3,即

(3)

2.2 PMMA样品表面电位的确定

入射电子能量为300 eV,Vg分别为-10、-5、0、5、10 V时测量得到的δ3随Vp的变化曲线,如图5所示。由图5可知,曲线的变化规律与图3、图4中仿真与验证实验的趋势相同。因此,按照前述方法找到拐点,确定出不同情况下的表面电位并在图5中用虚线标出。

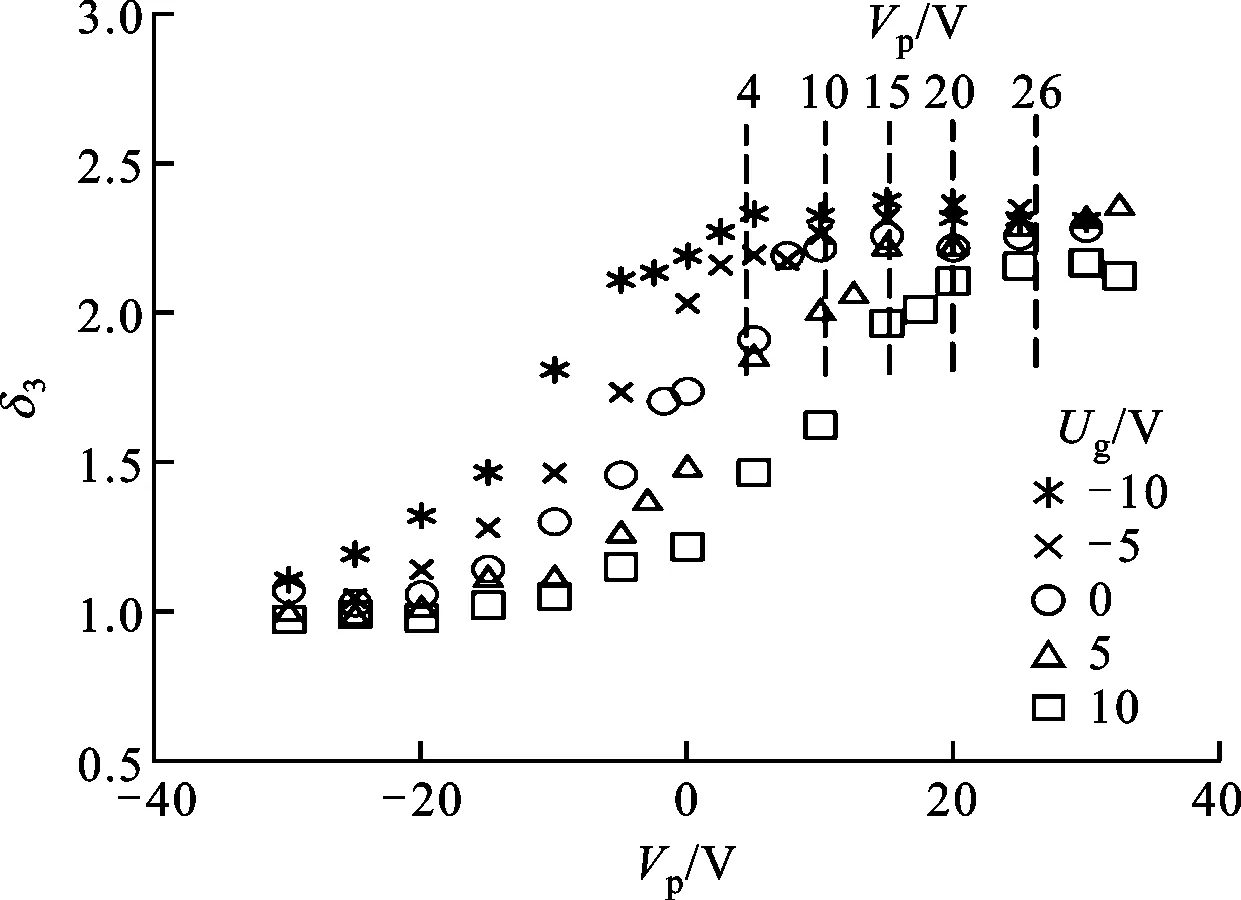
图5 PMMA样品在不同Vg下δ3与Vp的关系

探针的存在使得电场分布有一定的不均匀性,介质材料的表面电位会有一定的差别,所以严格地说,本文研究的表面电位是电子束轰击区域内样品表面电位的平均值。

2.3 栅网偏压对表面电位的影响

按照2.2节的方法测量入射电子能量EPE分别为100、200、300、500、700 eV时,Us与Vg的关系如图6所示。由图6可知,Us与Vg均可近似为线性关系。将数据点进行线性拟合后得到各直线的解析式,其斜率都在1附近。

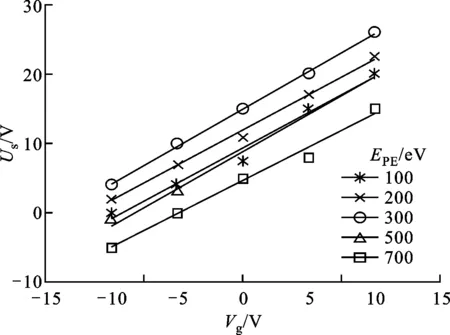
图6 不同EPE下Us与Vg的关系

在给定的Vg下对样品进行中和后,样品的表面电位达到稳定,此时二次电子发射系数为

(4)

式中:δ0为对应入射电子能量下,样品表面无拒斥场时(即Vg-Us≥0)的二次电子发射系数;N(E)为样品的二次电子能谱分布函数;E为二次电子的能量。由式(4)可知,当样品表面积累了一定的表面电荷后,在能谱曲线中只有能量高于Us-Vg的二次电子才可以被收集筒和栅网接收。测量SEY时,收集桶与栅网相连并且偏压较高为40 V(高于本文测量相应的样品表面电位Us),在入射电子能量固定的情况下,δ0不变,且与Us-Vg无关,说明能量高于Us-Vg的二次电子所占的比例固定。在入射电子能量固定的情况下,因为能谱分布N(E)本身与Us-Vg并不相关,所以只有当Us-Vg为一固定值时,才能保证式(4)成立,样品的Us与Vg成线性关系,且斜率为1,即

Us=Vg+a

(5)

这与测量结果相符,说明将探针法应用于介质材料表面电位的测量是可行的。

2.4 入射电子能量对表面电位的影响

不同Vg下Us与EPE的关系如图7所示。由图7可知,即使Vg不同,但是Us随入射电子能量的变化趋势是大致相同的,随着入射电子能量从100 eV增高到700 eV,Us都呈现出先升高后下降的关系,并用式(4)进行分析,随着入射电子能量的增加,二次电子发射系数δ0呈现先增大后减小的趋势,能量高于Us-Vg的二次电子所占的比例应先减小后增大。若能谱分布N(E)与入射电子能量无关,则当Vg确定时,Us变化趋势为先增大后减小,这与图7的实验结果相同,进一步证明了将探针法应用于介质材料表面电位的测量之中是可行的。

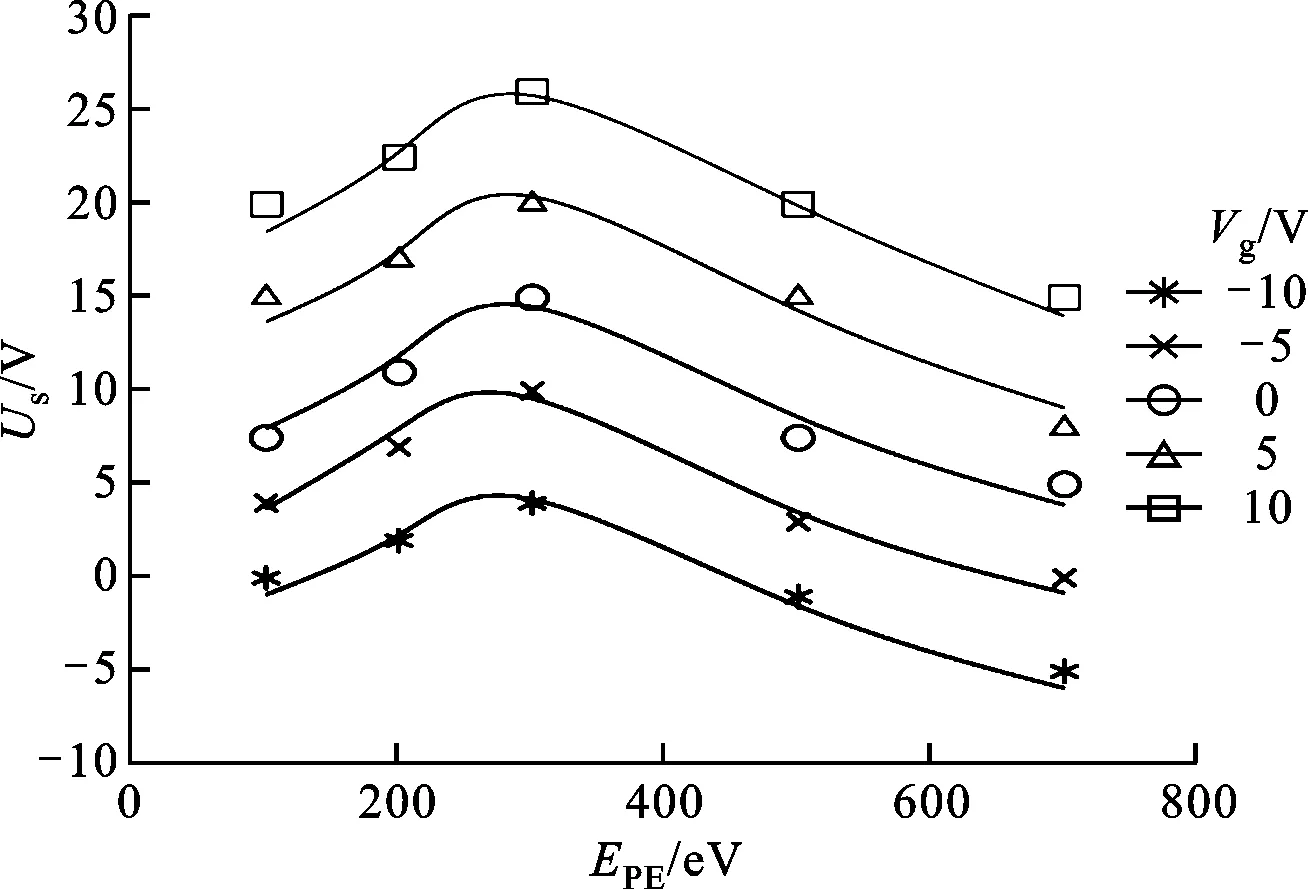
图7 不同Vg下Us与EPE的关系

3 误差的讨论

探针法测量样品表面电位时引起的误差来自于SEY的测量,而SEY的测量误差主要来自两个方面。

(1)由于介质材料SEY的测量必须建立在电子束以单脉冲照射的工作情况下,所以整个测量系统的脉冲响应是造成SEY测量误差的主要原因。在当前的实验环境下,除了尽可能提高系统响应速度之外,在读取示波器记录的脉冲电流时,可以读取脉冲电流的峰值,以尽量降低在测量过程中由于样品带电造成SEY下降而带来的测量误差。

(2)电子束照射样品时必然照射到探针,所以真正测量到的SEY并不是样品的SEY,而是样品与探针混合的SEY。此外,随着探针偏压的变化,电子束照射到探针那部分的比例也会相应的发生变化,这些因素都会引起SEY测量误差。一般而言,探针遮挡样品的几何面积越小,由探针带来的SEY的误差会减小,但是探针偏压对出射二次电子的影响也会随之减小,导致δ3与Vp关系中拐点越不明显。因此,在测量表面电位时,探针遮挡样品的几何面积与出现明显拐点之间需要进行优化选择。

4 结 论

基于介质材料SEY的测量,本文提出了一种简单易行的原位在线测量样品表面电位的新方法,即探针法。CST软件仿真和对金属样品的实验测量表明,这种方法的原理合理可行。在此基础上,本文将探针法应用于介质材料PMMA表面电位的测量之中,结果表明,在稳定状态下入射电子能量和栅网偏压对PMMA表面电位有直接的影响。随着入射电子能量的增加,PMMA表面电位呈现先升高后下降的趋势,PMMA表面电位高于栅网偏压时两者呈线性关系。研究分析表明,PMMA的带电程度与SEY、能谱分布密切相关。