WSNs 中基于TW-ToA 测量的目标定位算法*

刘 潇，倪艺洋

（江苏第二师范学院数学与信息技术学院，南京 210000）

0 引言

微型的、能量受限的具有数据感知能力的传感节点组成的无线传感网络WSNs（Wireless Sensor Networks）［1-2］已在医疗、环境监测、军事等领域得到广泛应用。这些应用均以节点有效地收集数据为前提，并且节点所感知的数据需配备准确的位置才具有价值，换言之，无准确位置的感测数据是无价值的。因此，WSNs 中的节点定位已成为研究焦点［3-4］。

而基于测距定位算法［5-6］受到广泛关注。现有多种测距技术，如（Different Time of arrival，DTOA）、角度信息（Angle of Arrival，AOA）以及基于接收信号强度（Received signal strength Index，RSSI）、双向时间到达（Two-way time of arrival，TW-ToA）。其中TWToA 测距算法中，目标节点记录信号传输时间［7］。尽管TW-ToA 测距算法对时钟偏差具有一定的强健性，但是它仍遭受因时钟差（Clock Skews，CSs）、不明的周转时间（Turn-around Times，TATs）问题而引起的测距精度下降问题。

目前，研究人员提出不同的基于TW-ToA 测距定位算法。文献［7］利用线性最小二乘LLS 估计CSs和目标位置，并利用回绕测试法（Loop Back Test）估计TATs。文献［8］提出基于欧式距离矩阵（Euclidean Distance Matrix，EDM）的协同定位算法，联合估计TATs 和目标位置。类似地，文献［9］引用半定锥规划（Semidefinite Cone Programming，SDP）估计目标位置。

尽管这些算法能够提高定位精度，但存在较高的计算成本。因此，本文所提基于双向到达时间测量的目标定位算法（Target Localization-based on TW-ToA，TL-TW-ToA），其目的在于平衡定位精度和计算成本。TL-TW-ToA 算法通过强健的平方测距、权重最小平方（Weighted Least Squares）标准将非凸问题转化成广义信赖域次优问题，再利用二分法获取解，进而消除缓解时钟偏差和周转时间（Turn-around Times，TATs）对定位精度的影响。

1 问题描述

在k 维无线传感网络中（k=1，2，3），存在N 个锚节点和一个目标节点，其中锚节点位置已知，而目标节点需利用测量与锚节点的距离估计自己的位置。假定x 表示目标节点位置、αi表示第i 个锚节点位置，且i=1，2，…，N。

目标节点依据TW-ToA 测距协议［10-11］测量离锚节点的距离。锚节点的处理时间称为TAT，通常是未知的。具体而言，第i 个锚节点所测量的TW-ToA时间表示为ti，其定义如式（1）所示：

对式（1）两边乘以c，并减去cμ'/2，可得测距模型，如式（2）所示：

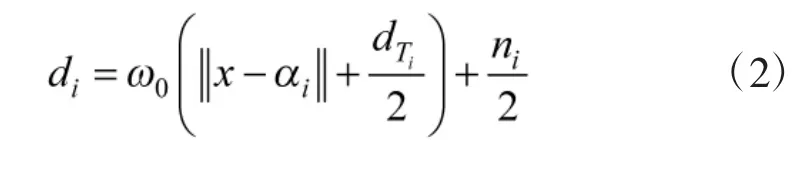
依据式（2）的测距模型，再利用文献［13］的最小二乘ML 估计，便可获取x、ω0和dTi的估计值：

然而，由于ML 估计为非凸、且无闭合解，无法直接求解式（3）。为此，引用ML 的近似估计，并且通过二等过程获取确认解。

2 TL-TW-TOA 算法

2.1 基于GTRS 的目标函数

本节利用所提出的TL-TW-TOA 算法估计目标位置，即利用TL-TW-TOA 算法求解式（3）。观察到式（3），由于未知数（N+k+1）高于观察数（N），因此，可利用一些近似算法求解式（3）。

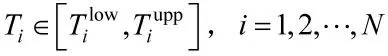
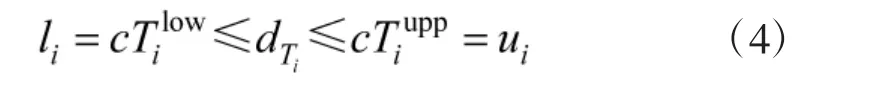
再利用式（2）可得：

因此，式（5）右边第2 项可转化为：

因此，式（5）可近似为：

考虑到ei值，并利用三角不等式，可将其转换不等式，如式（11）所示：

因此，依据式（11），式（10）可表示为：

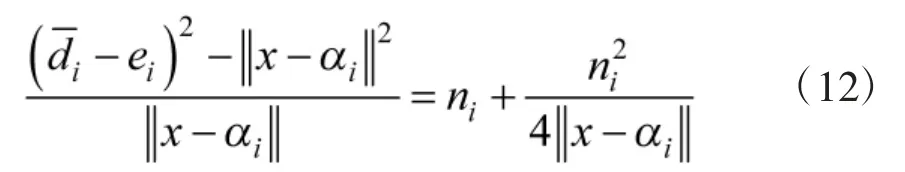
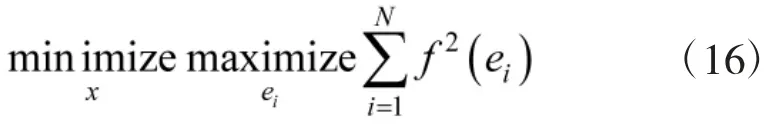
不直接处理式（15），而是求式（15）上限的最小值：

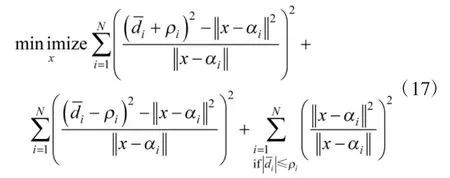
最后，便可得到GTRS［14］形式的解：

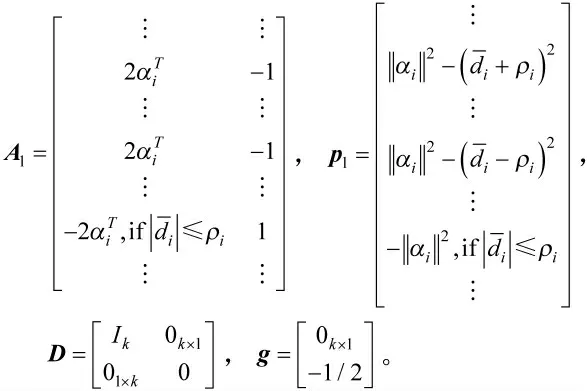
2.2 CS 和测距估计

其中，k 为迭代次数。

2.3 定位

3 性能仿真

3.1 仿真环境

利用MATLAB7.1 软件建立仿真平台，并进行Monte Carlo 实验分析TL-TW-TOA 算法的性能。在每个Monte Carlo 实验中，一个目标节点随机分布于［-B，B］×［-B，B］km2区域，且8 个锚节点的位置估计，且8 个锚节点位置分别为：［0.4，0.4］T，［0.4，-0.4］T，［-0.4，0.4］T，［-0.4，-0.4］T，［0.4，0］T，［0，0.4］T，［-0.4，0］T，［0，-0.4］T。

在仿真实验中，总运行的Monte Carlo 次数Mc=3 000。同时，CS 设定为ωi=1+δi，且δi在区间［-δmax，δmax］随机取值，且δmax=10-4。理想的TAT 设为T0=0.5 ms，K=30，光速c=3×108m/s。

同时，为了更好地分析TL-TW-TOA 性能，选择文献［7］的LLS 算法、EDM［8］、CCCP-SOCP［10］、SDP［9］、R-SOCP［11］和EGTR［12］进行比较。同时，EDM、SDP 和R-SOCP 利用MATLAB 软件的CVX编程工具实施。此外，引用均方根误差（Root Mean Square Error，RMSE）作为性能指标：

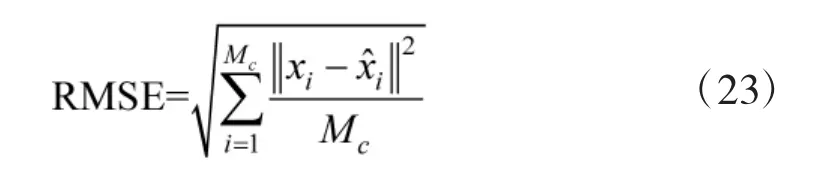
3.2 实验数据分析

首先分析噪声方差σi对RMSE 的影响，且σi从2～10 变化，锚节点数为8。实验数据如图1 所示。

从图1 可知，σi的增加，增加了RMSE，原因在于：σi的增加，增加式（2）的噪声值，加大误差项。此外，从图1 可知，EGTR、LLS 和EDM 算法的RMSE相近，远低于SDP、R-SOCP 和TL-TW-TOA 算法。相比于同类算法，TL-TW-TOA 算法的RMSE 是最低。这主要是因为：TL-TW-TOA 算法先利用GTRS获取定位模型，并充分考虑到TW-ToA 的CS 和TAT 时间。

接下来，分析锚节点数对RMSE 的影响，σi=6 m，锚节点数N 从5～8 变化，实验数据如图2 所示。

从图2 可知，锚节点数的增加，有利于RMSE的降低。这主要是因为：锚节点数越多，目标节点越容易获取离锚节点的距离信息。与EDM、SDP 算法相比，提出的TL-TW-TOA 算法的RMSE 得到有效控制。与R-SOCP 算法相比，TL-TW-TOA 算法的RMSE 并没有下降。但是，当锚节点数大于7 后，TL-TW-TOA 算法的RMSE 低于R-SOCP 算法。

最后，分析TL-TW-TOA 算法的复杂性，如表1所示，其中K 表示迭代次数，而N 表示锚节点个数。从表1 可知，TL-TW-TOA 算法的复杂度为3×O（KN），高于LLS 算法和EGTR，但是低于EDM 和CCCP-SOCP、R-SOCP 算法。

表1 算法的复杂度

4 结论

本文针对TW-ToA 测量的时钟偏差、周转时间问题，提出基于双向到达时间测量的目标定位算法TL-TW-ToA。TL-TW-ToA 算法将定位的凸优问题转化为广义信赖域次优问题，再利用二分法求解，进而降低了周转时间和时钟偏差对定位精度的影响。实验数据表明，提出的TL-TW-ToA 算法的定位精度优于同类算法，并且算法复杂度也得到有效控制。