弹道导弹列车遭核攻击下的生存能力建模分析*

代海峰，毕义明，刘 倩，韩慧华

（火箭军工程大学，西安 710025）

0 引言

核导弹铁路机动作战是陆基核力量部署的重要样式，自出现之日起就备受关注，这种设想最初由纳粹德国1937 年提出，其发展计划最终随着二战结束而失败。1959 年～1969 年十年间美国曾两次提出过导弹列车计划，虽开展了一些探索论证，但未进行实际部署。直到20 世纪80 年代，前苏联依托广阔的陆域纵深和完备的铁路网，率先部署了铁路机动作战样式的核导弹，文献［1-3］等研究普遍认为弹道导弹列车的出现大大增强了苏俄的陆基核力量，弹道导弹列车也被冠以“死亡列车”、“陆地核潜艇”等诸多极具恐怖和神秘色彩的称号。随着冷战的结束，俄罗斯铁路机动的核导弹2005 年退役。直到2014 年俄罗斯宣布重启弹道导弹列车计划（“巴尔古津”项目），并预计到2019 年部署5 个团的30 余套铁路机动作战系统，这种核作战样式又将重现于世。文献［4-7］表明在核导弹铁路机动作战样式的发展过程中，弹道导弹列车的作战效能和生存能力曾被不断评估和论证，其中生存能力的评估方法和过程总体来看较为粗糙，评估结果存在较大的局限性，因此，也遭受到很多质疑。由此出发，对弹道导弹列车遭核攻击下的生存能力建模分析很有意义。

1 弹道导弹列车生存能力定性分析

弹道导弹列车是铁路机动核导弹武器系统的结构主体和功能载体，是核导弹武器效能发挥的重要平台，其生存能力显得十分重要。在此，以部署弹道导弹列车的一方为A 方，对弹道导弹列车发动攻击的一方为B 方，由于弹道导弹列车武器系统属于战略重器，通常在两国核对抗的背景下运用，所以评估A 方弹道导弹列车的生存能力通常想定B 方采取的是核导弹攻击（其他攻击方式也具有威胁，在此不作讨论）。美国空军曾提出弹道导弹列车生存能力的设计战标是抵抗横向0.034 MPa 的冲击波超压，文献［8］研究认为在考虑最佳爆高和命中CEP 的影响下，0.4 Mt 和0.5 Mt 当量的核弹头将破坏约4.5 km 和7 km 铁路线上的列车。这些指标仅仅是从核爆炸毁伤能力和列车车体抗毁能力两方面来进行的粗略估计。

事实上，在战场条件下，影响弹道导弹列车生存能力的因素是复杂多样的。从A 方角度来说，弹道导弹列车的防护能力、机动能力、伪装能力、快速反应能力、行动策略和反导能力等直接影响弹道导弹列车的生存能力；从环境角度来说，地形地貌天候条件的好坏，电磁环境的利弊，交通条件，尤其是国家铁路网络的战时通达程度和保障水平会显著影响弹道导弹列车的生存能力；从B 方角度来说，侦察识别能力、核武器攻击的强度、核武器性能、攻击策略等给弹道导弹列车的生存能力造成严重威胁。弹道导弹列车遭受核攻击时，其毁伤有两方面，即直接毁伤和间接毁伤，直接毁伤包括：在毁伤半径内，核爆冲击波会摧毁列车主体结构、掀翻车体、破坏车厢内武器系统、杀伤作战人员等；核电磁脉冲则会毁坏车载电子设备和指控车厢内的信息系统等。间接毁伤包括：核攻击造成铁路毁坏、重要节点要道（铁路桥、岔路口）切断、山体塌陷、河流改道等等带来的二次毁伤。

B 方的核导弹攻击想定方面，根据攻击频次可分为：单次攻击和多次攻击，根据核攻击策略可分为点攻击和弹幕攻击，根据核导弹弹道末端是否可修正分为：可修正弹道型攻击和不可修正弹道型攻击。

通过以上定性分析，将B 方攻击武器设定为核导弹攻击，简化处理侦察探测环节和反导对抗环节，且适当忽略复杂环境和路况对生存能力计算的影响，为以下定量化建模分析奠定基础。

2 列车生存能力定量化建模分析

2.1 基础模型建立

2.1.1 弹道导弹列车实体建模

A 方弹道导弹列车车体为长条形状，假设列车有N 节车厢，每节车厢长度为l，列车机动速度为v，每节车厢根据功能不同，对列车的生存能力贡献度也不同，用贡献度因子ω 来表示。机动距离较大时，将每节车厢抽象为质点，质点位置为各车厢的几何中点，第i 节车厢质点坐标为（xi，yi），如图1 所示。

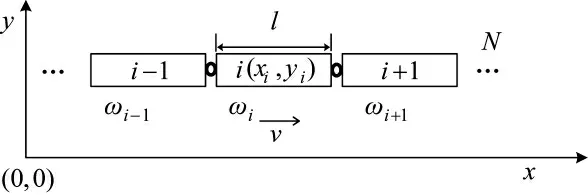
图1 列车实体模型

用抗毁概率来描述列车遭攻击后的保存实体，保持性能的能力。设列车总的抗毁概率为PKH，第i节车厢的抗毁概率为Pi，则满足公式：

对于各节车厢的重要度因子ω，作以下分析：假设弹道导弹列车系统具有“四个不确定”和“两个确定”，“四个不确定”：一是列车车厢数量不确定；二是各种功能类型车厢的重要度不确定（即因子ω 值不确定）；三是各种类型车厢数量比例不确定；四是各重要度不同的车厢在列车车厢序列中的位置不确定。“两个确定”：一是所有车厢的重要度加和为1；二是车厢类型数量为4 种，（即指控车厢、保障车厢、发射车厢、其他车厢）。通过以上分析，列车系统的这些不确定和确定混杂及定性定量转化问题，适合用云模型和相邻优属度熵权［9］的方法来统一分析，以获得每节车厢抗毁概率对于列车整体抗毁概率的权重值。基本步骤为：1）确定车厢集并用相邻优属度熵权法初步确定各车厢权重ωi'；2）建立车厢集的云模型并求加权综合云重心向量；3）用加权偏离度来衡量云重心的改变，建立评价评语集；4）根据云评测，获得各车厢权重最终取值ωi。

2.1.2 核爆冲击波毁伤模型

核攻击的毁伤效应主要有冲击波、核辐射和核电磁脉冲3 种，其中核冲击波是主要的杀伤效应，其能量释放可达核爆反应释放总能量的50%以上。一定距离上地面核爆（落点已知）冲击波超压经验计算公式为：

其中，Δp 冲击波超压值，d 为目标到爆心的距离，Q为核弹头当量。可见距离越大，冲击波超压值越小，假设存在毁伤临界距离r 和生存临界距离R，则核弹杀伤模型简化如图2 所示。

图2 核冲击波毁伤模型

再根据目标遭核弹攻击后生存概率计算的简化经验公式：

其中，RD为毁伤半径，CEP 为圆概率偏差。根据式（3）若给出毁伤临界概率和生存临界概率，可确定r和R。所以以距离关系来刻画的目标被毁伤概率PH公式为：

2.1.3 弹道导弹列车生存能力总体模型

弹道导弹列车生存能力以概率的形式来刻画为PSC，公式描述为：

其中，PZ为列车被侦察概率，PD为B 方攻击核弹抵达概率。B 方攻击核弹抵达概率是考虑了B 方打击决策变量和突防能力后的综合量化值。

2.2 典型核攻击想定下的生存能力

弹道导弹列车作为一种机动发射系统，当面临B 方核导弹攻击，弹道导弹列车生存能力的高低和列车与核弹落点的距离息息相关，若只考虑列车作单向匀速行驶，则这个距离的远近又可以用列车逃避攻击而行驶的时间Δt 来衡量。假若B 方来袭的核导弹不具备末端弹道修正能力，则其飞行的时间较长，在A 方有预警的情况下留给弹道导弹列车规避的时间Δt 较大，相反若来袭导弹具备末端弹道修正能力，则Δt 较小。在此先将这两种情况一并考虑，建立统一的描述模型。

2.2.1 单枚攻击

单枚攻击即B 方只发动一枚核导弹对A 方弹道导弹列车进行攻击。借鉴文献［9］中对曲线路径上的公路机动目标生存概率求解的作法，如图3所示。

图3 列车遭单枚核弹攻击图

图3 中曲线为导弹列车行驶的轨道线路，已知曲线方程为y=f（x），列车运行速度为v，列车初始时刻tc和机动规避后的时刻tz满足：tz-tc=Δt，为求列车第i 节车厢的初始位置C（xci，yci）和机动规避后位置Z（xzi，yzi），处理如下：假设第i 节车厢从C 点到Z点行驶的距离即曲线段弧长为S（x），则对于光滑曲线有：

式（6）与曲线方程y=f（x）联立可得曲线上任意一点的坐标为：

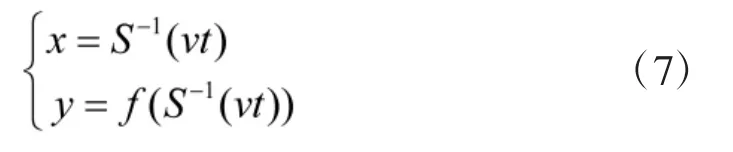
将tc和tz时刻代入式（7）可求得第i 节车厢的初始位置C（xci，yci）和机动规避后位置Z（xzi，yzi）。

假设B 方核导弹以列车第i 节车厢的初始位置C（xci，yci）为瞄准点，则其落点E（xe，ye）服从二维正态分布N（xci，yci；σ2；σ2；0），概率密度表示式为：

结合式（4），列车第i 节车厢的抗毁概率Pi为：

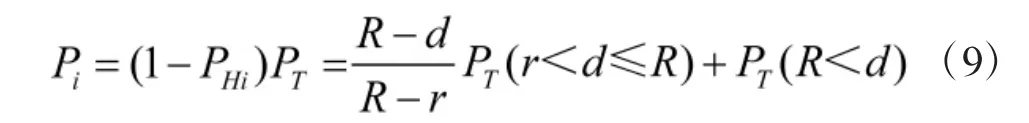
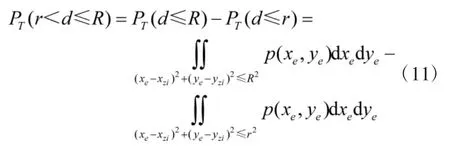
由于式（11）铺开较为冗长，基本方法与式（10）相同，在此不再赘述。根据以上分析，只需要给出列车机动时间Δt 和二维正态分布的方差σ，就可以求出列车第i 节车厢的抗毁概率Pi，根据2.1.1 中获得的第i 节车厢的重要度因子ωi，进一步结合式（1）和式（5）可求得列车总的抗毁概率PKH和生存能力PSC。其中，在B 方核导弹圆概率偏差CEP 已知的条件下，方差σ 可由经验公式：CEP=1.177 4σ 求得。

2.2.2 多枚连击

多枚连击是指B 方的多枚核导弹有先后的连续发动攻击，为简化研究，认为B 方目标毁伤评估和再探测过程耗时为零，即前一枚导弹攻击落地之后，若列车未被摧毁，则后一枚核导弹攻击立刻发起，且其瞄准点位为前一枚落地时刻A 方列车的坐标。如图4 所示。

对于B 方的前后两次攻击，假设两个攻击事件的概率计算相互独立，所以对于PHi取值条件的概率PT来说有：

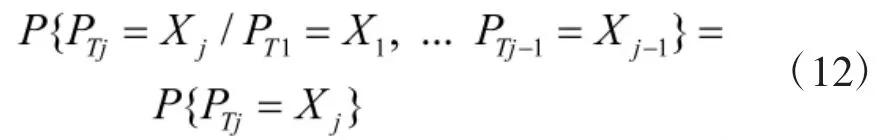
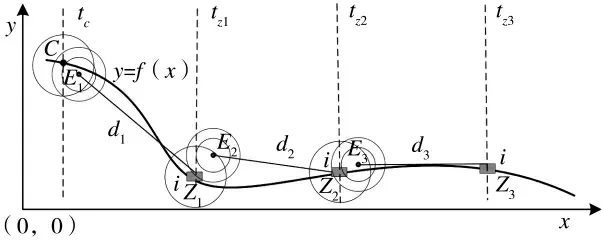
图4 列车遭多枚核弹连击图

所以每一次攻击后的生存概率都可以用2.2.1中的方法来计算，但是多枚连击的攻击方式会对列车的生存能力产生累积影响效应，例如两次攻击后的生存概率为：

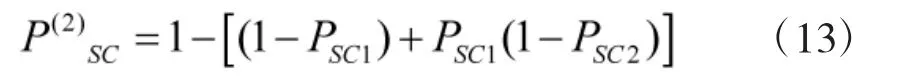
其中，PSC1和PSC2分别为第1 次和第2 次攻击后的生存概率。

则n 次攻击后列车的生存概率为：

其中，PSCk和PSCj分别为第k 次和第j 次攻击后的生存概率。

2.2.3 弹幕攻击

弹幕攻击又叫多枚同时攻击，是B 方对弹道导弹列车的机动区域进行面覆盖式的打击。若多枚核弹落点较近，落地时间相差不大，通常存在互毁效应。对此先建立不考虑互毁效应的导弹列车生存概率计算模型，而后再加上互毁效应带来的约束条件，进行方程联解即可。

由于先不考虑B 方核弹头间的互毁效应，则列车机动区域均会同时遭受打击，在不考虑其他特殊路段情况（例如山体隧道掩护）的条件下，列车的机动规避对自身的生存没有意义，只是列车机动的速度不同，会影响B 方对其机动区域大小的判断，进而攻击耗弹量也会有所改变。

对B 方导弹的落点分布的分析如下：落点区域为以轨道线路为中心的条带如图5 所示。

图5 列车遭核弹弹幕攻击图

从横切面来看服从一维正态分布N（yci，σ2），其分布密度函数为：其中，σ 的值可以2.2.1 中提到的方法CEP=1.177 4σ来确定。而沿曲线方向则服从弧段［ci，zi］上的均匀分布，分布密度函数为：

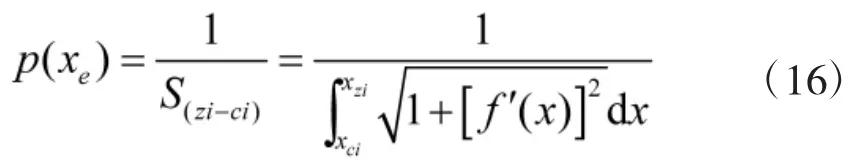
所以核导弹在条带上的分布即为一个联合分布，假设沿曲线方向的均匀分布与横切面的正态分布相互独立，则联合分布密度函数为：

之后求取每一枚核弹攻击后列车总的抗毁概率PKH和生存能力PSC方法与2.2.1 相同。

最后，求m 枚核弹进行弹幕攻击后的导弹列车生存概率PSC（m）为：其中，PSCi为第i 枚核弹攻击后导弹列车的生存概率。

在以上模型的基础上，如果考虑互毁效应，假设B 方在规划核弹落点时，存在距离约束条件或时间约束条件为：

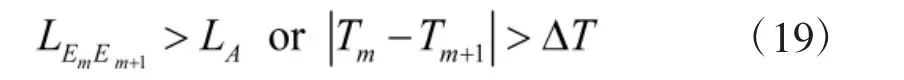
所以结合式（18），弹幕攻击下导弹列车生存概率计算总体模型为：

综合以上模型的分析，计算导弹列车在各种典型攻击想定下生存能力时都受到列车机动规避时间Δt 的影响，所以在其他变量合理设定的情况下，Δt 即为求解导弹列车生存能力的关键参数，而Δt的大小与B 方核导弹是否具备末端修正能力相关。

3 算例分析

3.1 计算结果

假设给定如下参考数据：B 方核弹头当量为0.3 Mt～10 Mt，弹道可修正的核弹攻击下，导弹列车可规避机动的时间Δt 为3 min～6 min，弹道不可修正的Δt 为30 min～60 min（不考虑B 方杀伤链其他环节的时延），借鉴文献［5，7］，设导弹列车机动速度为50 km/h～100 km/h，列车车厢数为6 节～8 节，计算结果见图6 ～图10（其中矩形点表示不可修正弹道的攻击，三角形点表示可修正弹道的攻击）。

图6 当量0.5 Mt 的单枚攻击（1 枚）

图7 当量0.5 Mt 的多枚连击（4 枚）

图8 当量0.5 Mt 的弹幕攻击（10 枚）

图9 当量0.5 Mt 的弹幕攻击造成列车0.9 的毁伤概率

图10 弹幕攻击造成速度60 km/h 的列车0.9 的毁伤概率

3.2 结果分析

综合分析图6 ～图8 可见，在B 方核弹头当量和其他条件一定时，A 方导弹列车遭受3 种攻击方式的生存概率随其机动速度的增加而增加，说明适当增加列车速度，有利于列车的生存。而且可以看到，B 方弹道可修正的攻击比弹道不可修正的攻击，A 方列车生存概率更小。此外，如果忽略耗弹量，B方单枚攻击的方式对列车的生存威胁较小，尤其是不可修正弹道的攻击，对机动的列车几乎不具备打击能力。相比之下，多枚连击较好，而弹幕攻击的方式在确保毁伤方面更具优势，同时，弹幕攻击在一定条件下可降低对弹道修正的要求。

进一步观察图9 可知，攻击核弹当量一定时，B方对A 方的导弹列车造成0.9 的毁伤概率所需的耗弹量随列车机动速度的增加而增多，同时也体现出弹道可修正与否的区别。观察图10 可知，当列车机动速度一定（60 km/h）时，B 方对A 方的导弹列车造成0.9 的毁伤概率所需的耗弹量还与核弹的当量有关，当量较大时，达到同等毁伤效果的耗弹量可适当减少。

4 结论

采用定性与定量相结合的方法，先通过对导弹列车生存能力影响因素的定性分析，提取主要因素并对一些条件作了限定，而后建立定量描述模型和几种攻击想定之下的生存能力计算模型。最后设置合理参数，计算结果并绘图，对其作了详细的分析。通过建模分析，能对弹道导弹列车这种复杂的武器系统的生存能力进行有效的量化评估，可为列车战场生存能力综合评估提供参考。

本文的研究未考虑列车变速、变向和车厢分节机动问题，铁路线路较为简单，没有考虑一些复杂路况，B 方攻击条件也被限制为核导弹攻击，而且导弹列车的战场生存能力应该是一个交战双方动态对抗的过程，其中还会掺杂大量不确定的因素，这也会影响导弹列车的生存能力，在这种情况下，文献［11］基于作战过程的生存能力评估的思路是值得借鉴的。