基于主客观组合赋权的PSSA 安全性指标分配方法

柳 平，延 黎，刘东亮，赵树恩，宋 刚

（1.重庆交通大学航空学院，重庆 700074；2.解放军95949 部队，河北 沧州 061736；3.重庆交通大学机电与车辆工程学院，重庆 700074；4.解放军61255 部队，山西 侯马 043000）

0 引言

欧美发达国家在军用和民用飞机的系统安全性设计中有较为完善的规范和流程，其中规范包括MIL-STD-882E，MIL-HDBK-516B，SAE ARP4761和SAE ARP4754 等［1-3］。飞机系统安全性设计和验证采用“V”字型流程，包含了飞机功能危险分析（FHA）、初步系统安全性评估（PSSA）、系统安全性评估（SSA）等环节［3-4］。其中，初步系统安全性评估（Preliminary System Safety Assessment，PSSA）是飞机安全性设计的关键环节，也是第一个定量化的环节，主要用来确定故障如何导致功能危险分析（FHA）中的功能危险，以及确定FHA 提出的安全性要求怎样被满足。PSSA 最为核心的问题是所建故障树的安全性指标分配问题。目前，安全性指标分配是由工程人员根据主观判断或类比法得出，具有较大的主观性，亟需一种可以综合历史数据和主观分析的定量研究方法。

区间层次分析法（IAHP）［5］具有容易理解、直观、计算方便等特点，是一种常用的主观评价方法。粗糙集理论（Rough Set，RS）是处理不精确、不一致和不完整等各种不完备信息的有效工具，具有不需要先验知识、数学基础成熟、易用性强等特点，与处理其他不确定问题的理论具有很强的互补性［6］。主、客观组合赋权法具有既能客观反应各指标的重要性，又能反应决策者主观愿望的优势，近年来得到了广泛应用［7］。针对PSSA 安全性指标定量分配的难点问题，本文提出了一种基于主客观组合赋权的初步系统安全性评估（PSSA）安全性指标分配方法，应用粗糙集理论（RS）和区间层次分析（IAHP）法分别确定客观和主观权重。

1 PSSA 的主、客观指标权重计算方法

1.1 基于IAHP 的主观指标权重计算方法

指标体系中的主观指标具有不确定性，而区间层次分析法（IAHP）［5］处理不确定性的决策信息，具有容易理解、直观、计算方便等特点，因此，本文采用该方法来确定定性权重。

表1 判断矩阵比较尺度表

1.2 基于粗集可辨识矩阵的客观权重确定

粗糙集理论最先由波兰科学家Pawlak 提出，其最大优势是无需提供除问题所需处理的数据集合之外的任何先验信息。此外，粗糙集的另一个优势是能够有效地去除冗余［9-12］。在PSSA 安全性指标分配中，获取的各分项的权重值往往是连续的，是一个具体概率值。而由Z Pawlak 提出的以不可分辨关系为核心的粗糙集方法处理的是离散属性值，因此，在PSSA 安全性指标分配中应用粗糙集理论时，必须将连续值进行离散化。离散化方法都应尽可能满足以下两点［13］：1）属性离散化后的空间维数应尽量少；2）属性值被离散化后丢失的信息尽量少。

为了计算过程的简便，本文采用等宽度离散化方法进行连续属性值的离散化。等宽度（Equal Interval Width）离散化方法就是将连续属性值分成k个等宽度的值域。离散间隔数由决策者根据实际的数值确定，则每一区间的宽度为

式中，vmax，vmin分别表示连续属性值的最大值和最小值。这样，t 构成了一个区间的边界，也称阀值，每一个区间中的值为vmin+it（i=1，2，…，k-1）。

可辨识矩阵（Discernibility Matrix）是粗糙集理论中的一个重要概念，这种表示方法具有许多优点，特别是用它可以方便地解释和计算信息系统的核和约简。文献［13］提出了利用可辨识矩阵计算属性重要性的方法，为权重的确定或属性约简提供了一种简便有效的方法。

定义：令S=（U，A，V，f）是一个知识表达系统，|U|=n。S 的可辨识矩阵是一个n×n 的矩阵，其任一元素为

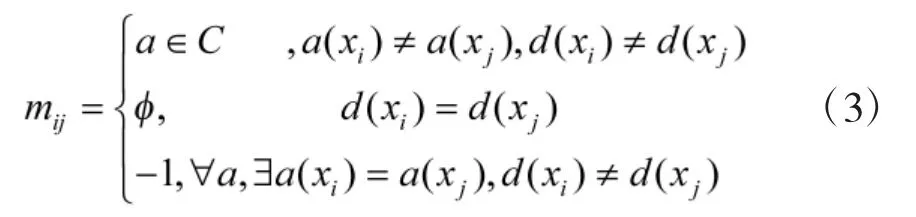
式中，a（x）是对象x 在属性a 上的值，d（x）是记录x在D 上的值。

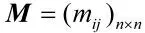
2 主客观组合赋权的安全性指标分配

为了尽量降低主观赋权法和客观赋权法各自带来的权值偏差，以下采用一种基于离差平方和的组合赋权方法［7，14］，将IAHP 法计算所得的主观权重和粗糙集方法计算所得的客观权重进行优化集成，计算最终权重。

其中，θ 为对主观赋权结果的信任度；1-θ 为对客观赋权结果的信任度；表示第j 个指标属性的权重。最优化模型式（5）存在最优解，其中

基于前面对指标权重确定方法的研究，本文提出基于主客观组合赋权的PSSA 安全性指标分配方法，如图1 所示。

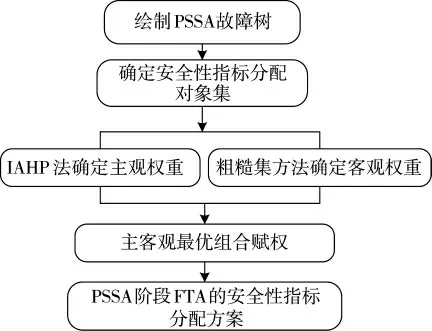
图1 PSSA 阶段FTA 安全性指标分配流程

具体步骤如下：

2）利用区间数特征向量法确定主观权重。根据表1 的指标比较尺度，确定区间数判断矩阵，运用IAHP 法计算各指标a（jj≤m）的权重向量。

3 PSSA 指标分配应用案例分析

某新型飞机的设计采用了系统安全性的流程和方法。其中，普遍采用了故障树（FTA）进行安全性分析。传统的PSSA 安全性指标分配方法是按照主观经验和类比法开展。本节采用第1 节的理论和第2 节的具体步骤，基于9 型同类飞机的经验数据开展案例分析。

以该型飞机“丧失对两个平尾的滚转控制功能”为例建立PSSA 的故障树模型（如图2 所示），以第1 层安全性指标分配为例进行研究。造成“丧失对两个平尾的滚转控制功能”顶事件的可能原因事件主要包括：动作筒卡死、驾驶杆失效、直流电源功能完全丧失、两套液压系统全部失效和左右平尾位置指示功能丧失5 类事件。

图2 “丧失对两个平尾的滚转控制功能”的FTA 模型

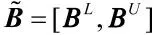
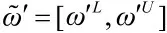
根据第2 节的步骤3），属性集C 为动作筒卡死、驾驶杆失效、直流电源功能完全丧失、两套液压系统全部失效、左右平尾位置指示功能丧失5 项指标，论域U 为选取的9 型飞机的设计可靠性指标，其设计可靠性指标如下页表3。

为了计算简便，这里采用式（1）等宽度离散化方法进行连续属性值的离散化处理，将各分项性能的取值分为好、中、差3 个等级，分别用3、2、1 表示，这样就建立了一个离散化二维信息表S=（U，A，V，f），见表4 所示。

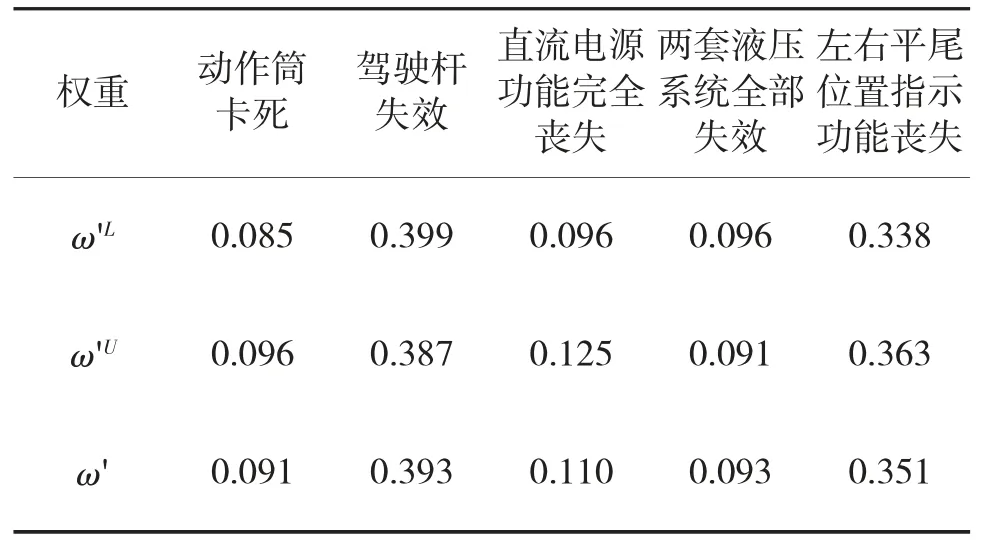
表2 各指标主观权重系数

各指标得权重系数排序为：驾驶杆失效＞左右平尾位置指示功能丧失＞电源完全丧失功能＞动作筒卡死＞两套液压系统全部失效，可见，驾驶杆失效和左右平尾位置指示功能丧失所占权重较大，安全性指标分配结果符合实际。“丧失对两个平尾的滚转控制功能”属于灾难级（Ⅰ级），因此，其顶层的安全性根据文献SAE ARP4761“FHA 的等级划分标准与概率要求”可得为：＜10-9/h。设该型飞机对于出现“丧失对两个平尾的滚转控制功能”的顶事件可接受指标定为0.9×10-9/h，则安全性指标分配结果如表6 所示。

表3 9 型飞机可靠性指标数据

表4 PSSA 安全性指标分配信息表

表5 各指标客观权重系数和最优组合权重系数

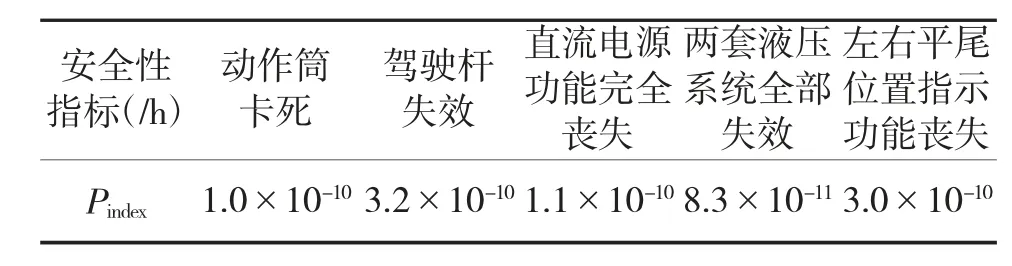
表6 PSSA 安全性指标分配结果

4 结论

当前我国新型民用和军用飞机均开展了系统安全性设计，其中涉及一些核心理论方法亟待突破。本文针对飞机系统安全性设计流程中PSSA 安全性指标定量分配的难点问题，综合采用粗集可辨识矩阵、区间层次分析法、主客观组合赋权等方法，提出了PSSA 安全性指标定量分配的一套方法步骤，以某型飞机“丧失对两个平尾的滚转控制功能”为例进行了案例分析和验证。本方法具有较强的可行性，在飞机系统安全性设计中具有良好的工程应用前景。