基于双层Voronoi 图的常规导弹多波次打击模型

吴闰平，刘卫东，杨 萍，陈 鹏，李晨旭

（火箭军工程大学，西安 710025）

0 引言

随着军事科技的高速发展，导弹武器作为集地理学、物理学、计算机科学、化学、材料学和军事战略学为一体的高科技作战武器，作战距离远、隐蔽性强、威力大，已经成为各国作战的首选方式。在导弹武器作战方式中，大弹量、多波次的常规导弹打击策略成为当下主要研究方向之一。这就涉及到了作战区导弹部队的任务分配与机动问题。常规导弹多波次打击流程为：中心库装弹→待机阵地待机→发射阵地第1 波次发射→转载阵地第1 次转载→发射阵地第2 次发射→……→发射阵地第n 次发射，在机动过程中，如何合理安排各个发射装置的机动路径与相应阵地，使的机动路径总体较短，暴露时间最短，降低被敌侦查设备发现的概率，以增大生存概率具有重要意义。

在之前的常规导弹多波次打击问题的研究中，汪民乐［7］研究了多波次对地攻击的火力分配问题；王桐［9］运用马尔科夫链解决了多波次打击敌方目标的效果评判问题；杨萍［5］运用军事运筹学与不确定理论，对多波次导弹打击的战前运输问题进行了建模分析，王鹏［11］根据军事公路运输的特点，建立了基于GIS 的路线选择模型，给出了相应的求解方法。总体来看，前人所做的研究主要集中在导弹发射装置的机动路径优化方面，以及在给定机动路径的基础上进行机动调度，解决了多波次导弹作战的路径规划与机动调度基本问题。但以上研究基本都是对于较小规模作战路径选择调度的研究，而对于大弹量、多波次打击中的发射装置机动问题研究较少。且使用全局优化搜索方法会使得算法复杂度增加，算法效率降低，因此，本文首先采用双层Voronoi图模型对发射阵地进行了动态聚类，由专门的转载阵地对其发射阵地转载服务，将多中心优化问题转化为单目标优化问题。其次建立双层规划模型，上层使的总体机动路径最短，下层使的第1 波次发射完毕后，导弹发射装置从发射阵地到转载阵地再到发射阵地的机动距离最短，最后设计了适用于此问题的遗传算法进行了求解。

1 基于双层Voronoi 图的发射阵地动态聚类

Voronoi 图模型对于解决较大规模的路径优化问题具有较大优势，本文运用双层Voronoi 图模型对各个发射阵地进行聚类，并通过双层规划理论构建多波次发射路径全局优化模型，并使的整体算法复杂度降低，得到最佳的机动路径。

1.1 Voronoi 图构建方法

本文通过构建Delaunay 三角网的方式建立Voronoi 图模型，步骤为：

1）离散的发射阵地自动构建Delaunay 三角网。对离散的发射阵地和形成的三角形进行编号，并记录每个三角形是由哪3 个离散的发射阵地构成的。

2）计算并记录所有三角形的外接圆心。

3）遍历三角形链表，寻找与当前三角形的三边共边的相邻3 个三角形。

4）如果找到，则把寻找到的三角形的外心与该三角形的外心连接，存入维诺边链表中。如果没有找到，则求出最外边的中垂线射线存入Voronoi 边链表中。

5）遍历结束，所有Voronoi 边被找到，根据边画出Voronoi 图。

生成Voronoi 图的基本方法是构建Delaunay 三角网，基本步骤为：

1）将所有的发射阵地构建超级三角形，并放入三角形链表。

2）将发射阵地依次插入，找到可以将此发射阵地包含的两个已存在的三角网的外接圆，删除公共边，并将新插入的发射阵地与其余4 个发射阵地连接，形成新的Delaunay 三角形链表。

3）对新形成的三角网进行优化设计，并置入Delaunay 三角形链表。

4）重复第2）步，使得所有发射阵地插入。关键步骤2）的实施流程如图1 所示。

图1 Delaunay 三角形实施流程

1.2 转载阵地双层Voronoi 图模型

1.2.1 建立双层Voronoi 图

本节通过引入一个点和一条线的K 环Voronoi邻居的概念来介绍双层Voronoi 图，如下页图2 分别表示两个不同发射阵地的Voronoi 距离，一个点的Voronoi 邻居以及一条线的Voronoi 邻居。

建立双层Voronoi 图，上层Voronoi 图粗略地定义了每个转载阵地的初始覆盖区域，较低层次的Voronoi 图定义了发射阵地的Voronoi 邻居，这有助于通过将局部搜索空间限制为K 环Voronoi 邻居来优化每个转载阵地的发射装置路线问题。

1.2.2 算法实施

通过BVDH［1］算法对此问题进行求解，算法基本步骤为：

1）求解初始解

得到此问题的初始解，如果发射阵地位于上层转载阵地Voronoi 图的Voronoi 区域，则该发射阵地最初被分配到该转载阵地。分配给转载阵地的发射阵地的路线通过单个转载阵地的“集群优先，路线优先”VRP［2］算法生成。

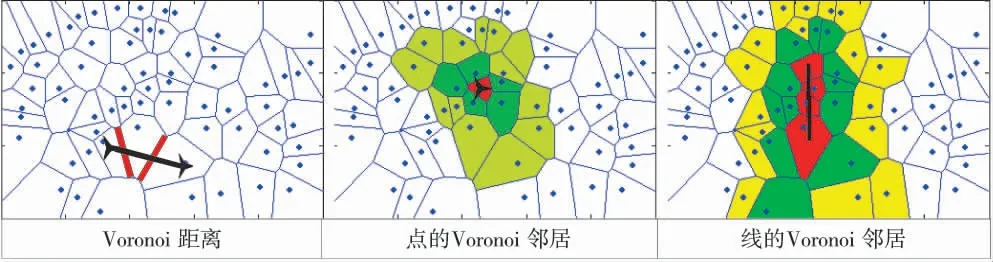
图2 Voronoi 图

图3 双层Voronoi 图模型

2）初始解改进

运用SA 算法改进初始解，改进阶段分为两部分，为在一个转载阵地的范围内的路线和转载阵地之间的路线。首先为了改善一个转载阵地范围内的路线，该算法通过将局部搜索空间限制为K 环Voronoi 邻居内并使用3 个流行的邻居结构1-0 交换移动，1-1 交换移动和2-opt 移动［3］来将发射阵地从一个路线重新排列到另一个路线。其次为改善在转载阵地交汇间的发射装置路径，本文采用1-0交换方式和1-1 交换方式对初始解进行改进，这两种方式是在上层Voronoi 图的Voronoi 边缘的K 环Voronoi 邻居中实现的。不选用2-opt 移动是因为它可能会在站点上生成许多路由而增加当前解决方案的总路线长度。算法改进过程如图4 所示。

图4 SA 算法改进步骤

BVDH 算法流程如下页表1 所示。

3 双波次打击双层规划模型建立

3.1 模型建立

本文以双波次打击为例，建立双层规划模型，上层为整体最短机动路径，下层为从第1 波次发射阵地到达转载阵地进行转载并机动至第2 波次发射阵地进行第2 波次发射的最短路径。即

表1 BVDH 算法流程

其中，l1与l2分别表示第1 波次与第2 波次总的机动距离表示a 类发射装置k 从待机阵地d 到发射阵地f1的距离；表示a 类发射装置k 从发射阵地f1到转载阵地z 的距离；表示a 类发射装置k从转载阵地z 到发射阵地f2的距离；为1 时表示a 类发射装置k 从待机阵地d 到发射阵地f1，为0 时表示a 类发射装置k 未从待机阵地d 到发射阵地f1；为1 时表示a 类发射装置k 从发射阵地f1到转载阵地z，为0 时表示a 类发射装置k 未从发射阵地f1到转载阵地z；为1 时表示a 类发射装置k 从转载阵地z 到发射阵地f2，为0 时表示a 类发射装置k 未从转载阵地z 到发射阵地f2。

在第1 波次齐射过程中，每个发射点位的使用不得超过一次：

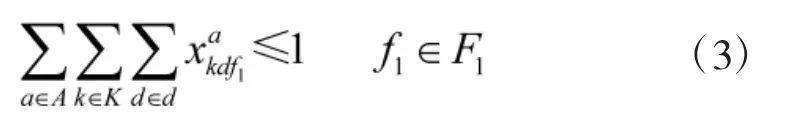
在第1 波次齐射完毕后，通过在转载区域转载后到达第2 波次发射点位，发射阵地只能使用一次：

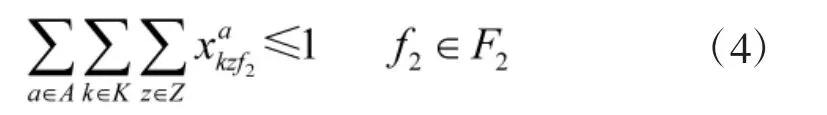
第1 波次与第2 波次发射点位不得重复：

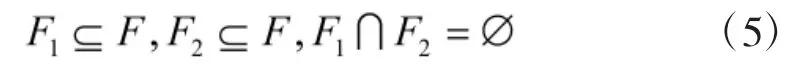
同一时刻，转载阵地容纳的发射装置数量上限为s

其中，s 表示转载阵地可以同时作业的发射装置的数量，对于给定的作战对象，s 是已知的。参与作战的发射装置总数少于各个待机阵地的发射装置的总数

其中，S 表示发射装置的总数，对于给定的作战对象，S 是已知的。构建双层规划模型为：

3.2 算法设计

设计适应于此问题的遗传算法求解最佳的机动路径并进行机动调度，算法流程为：

Step1：确定染色体配置方案。将两个波次的打击任务分别定义为第1 波次发射编码段，第2 波次发射编码段及转载阵地编码段如图5 所示。

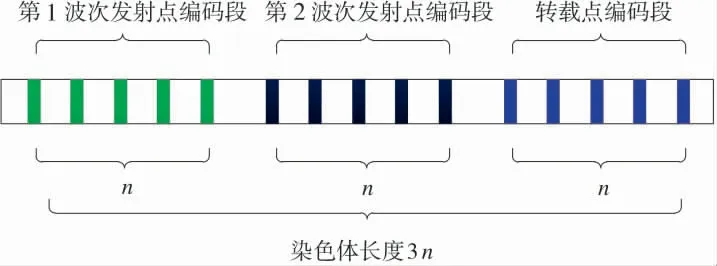
图5 染色体编码图

Step2：确定目标函数。对于不同的发射装置，不同的道路情况，求解出所有发射装置的最短机动路径；以所有发射装置的最短机动路径为适应度函数，并使得两个波次发射点位于同一转载阵地的服务区内，通过求解最小适应度值来搜索最优的机动方案。染色体编码如图6 所示。

图6 染色体编码图

Step3：算法适应性改造

1）随机初始化种群方案；

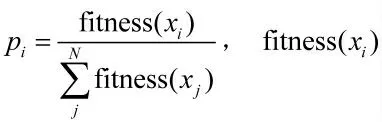
3）交叉。从种群中随机选取两个个体，首先根据交叉概率判断是否交叉，然后进行交叉操作。当需要对发射阵地进行交叉时，首先判断需要交叉的发射点是否与本染色体的发射点基因重复，如果重复，则放弃交叉操作；

4）变异。从种群中随机选择一个个体进行变异，当需要对发射阵地变异时，首先判断发射点位是否重复，如果重复，则放弃变异；

5）算法实施。根据遗传算法特点及本问题的特殊性，建立算法实施框架如图7 所示。

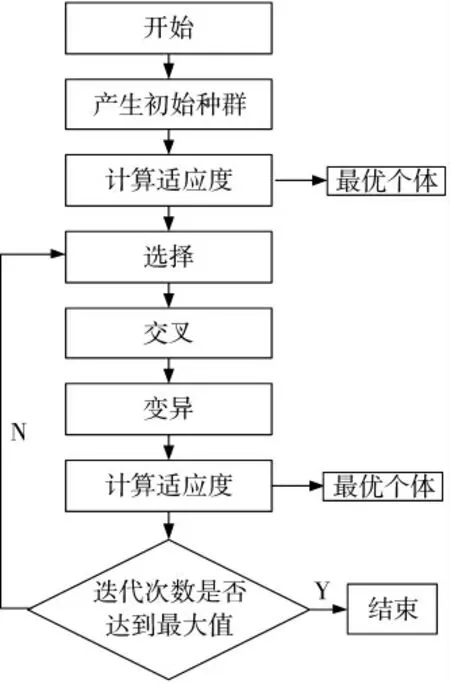
图7 算法流程图

4 算例分析

对于有2 个待机阵地、5 个转载阵地、60 个发射阵地及62 个道路节点的给定路网如图所示的具体路网进行两个波次打击问题的路径规划，每个波次使用24 辆发射装置。其中，各个节点分别表示待机阵地（D）、转载阵地（Z）、发射阵地（F）和道路节点（J），蓝色的道路表示单行道，红色的道路表示双行道。

图8 作战路网

第1 阶段：得出初始解［12］。

创建转载阵地、发射阵地的Voronoi 图以及发射阵地分布线的K 环Voronoi 邻居。得出每个转载阵地对于发射阵地的初始配属如下页图9 所示。

初始阵地配属关系如下页表2 所示。

初始机动方案如表3 所示。

机动总距离为5 017.231 km。

第2 阶段：改进阶段。

运用Voronoi 图算法改进后的阵地配属关系如表4。

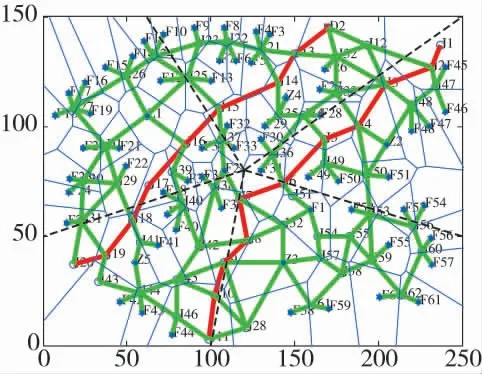
图9 阵地初始配属图

表2 初始阵地配属

表3 初始机动配置

表5 改进机动配置

改进后的机动方案如表5 所示。

机动总距离为4 352.837 km。相比初始方案减少了15.26%。

5 结论

常规导弹多波次作战过程中合理高效的波次转换是取得战争主动权的有效方式，针对全局优化过程中出现的算法复杂度高，优化效率低的问题，建立常规导弹多波次打击时发射阵地与转载阵地的双层Voronoi 图模型，对各个发射阵地归属于某一特定的转载阵地，将多中心优化问题简化为单中心优化问题。在此基础上构建上层为全局最短路径下层为第2 波次最短路径的双层规划模型，设计适合于此模型的遗传算法，有效降低了算法的复杂度，求解效率较高。