基于光流的组织应变估计算法
【作 者】辛莉莉,张勇德
中国医科大学公共基础学院,沈阳市,110122
0 引言
通常,正常组织和病灶组织之间存在弹性差异,而这种差异在弹性成像模式中清晰可见,超声弹性成像这种能反应组织力学属性的性能弥补了医学成像模态的不足[1-2],在近些年得到了迅速发展。
超声弹性成像按照组织激励方式的不同可分为准静态弹性成像和声辐射力弹性成像等[3]多种方式,其中准静态弹性成像是最基本的方法,很多其他方式的超声弹性成像也是用同样或类似的方法进行位移估计或者应变估计[4]。在准静态超声弹性成像中,当用探头对组织施加压力时,组织作为一种线弹性体[5],不仅有平移运动,而且还有形变。基于位移梯度的准静态超声弹性成像算法可分为两步:假设局部组织运动只存在平移,首先计算压缩前、后射频回波信号在时域上的相对位移;根据相对位移利用差分求出组织应变[6]。该类算法一般都假设压缩后的信号是压缩前信号的时移,忽略了形变。当信号形变较大时,会出现严重的去相关,进而导致位移估计过程中会引入去相关噪声,而位移到应变的差分过程会进一步放大噪声[7]。因此,该类算法的应变图像质量较差,信噪比低。
仿射变换是一种六参数组织运动模型,它综合了平移、旋转、缩放、切变等线性变换[8-9],既包含了位移,又包含了形变,更符合局部组织运动,而且基于该模型的算法可以同时得到位移和应变信息,避免了位移到应变的差分过程对噪声的放大。
光流法是运动估计的重要算法之一,光流计算是利用相邻两帧图像中像素强度信息的时域变化和相关性来确定各个像素的运动[10-11]。光流法本身有良好的并行性,并且可得到亚像素单位的位移[12]。该研究综合了仿射变换和光流法,在先验估计的思想下[13],在小范围内进行运动追踪,提高了算法成像质量和运行速度。
1 方法
1.1 光流法
光流法实际上是一种根据要检测图像像素灰度随时间的变化来了解物体的移动速度和方向的手段[10]。根据图像灰度一致性假设,可推导出光流的基本约束方程。在光流基本方程的基础上,HORN和SCHUNCK[11]提出了全局平滑性约束;LUCAS和KANADE[10]引入了局部平滑约束,即假设在一个很小的空间邻域内光流保持恒定。在一个小的空间邻域上,假设邻域内数据点个数为n,对不同的点赋予不同的权值,光流估计误差为:
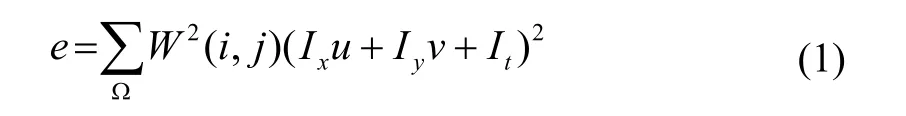
其中,Ix,Iy,It是图像灰度在x,y,t方向上的偏导数,u,v是像素在x,y方向上的位移,由此可知,式(1)只有两个未知运动参数,即光流法是假设组织在施压时的局部运动是平移运动。
在准静态超声弹性成像中,当用探头对组织施加压力时,以探头为参考点,与探头直接接触的区域相对位移较小,满足光流法的基本约束条件,可直接用光流法进行计算。随着深度的增加,组织与探头的相对位移也增加,尤其是远离探头的边缘区域,形变较大,此时如果直接用光流法进行估计,成像质量差。
1.2 改进措施
为了补偿压缩后信号的形变影响,CESPEDES等[14]提出对压缩后的信号进行拉伸,从而增加压缩前后信号的相关性。但是该补偿措施是在组织局部的运动为平移的假设条件下进行的,忽略了组织的形变,即使对信号进行补偿,最后估计的运动也存在误差。
1.2.1 仿射变换模型
仿射变换是一种组织运动模型,可用来估计组织运动[15-17]。假设点A是某一窗口的中心点,B是窗口内的除中心点的任意一点,A’是窗口形变后的中心点,B形变后是B’。B到B’的形变可以用仿射变换来表示[17]:
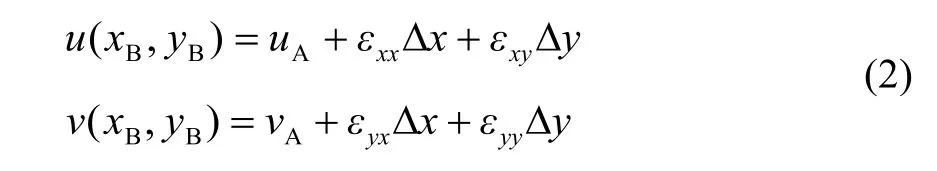
其中,xA和yA,xB和yB分别表示点A和点B在x轴和y轴的坐标,Δx=xB-xA,Δy=yB-yA表示A和B在x方向和y方向的距离,εxx, εxy, εyx, εyy分别表示横向应变,横向剪切应变,轴向剪切应变和轴向应变。该算法可同时得到位移和应变信息。
把仿射变换等式代入到式 (1) 中即可得到新算法的基本方程:

此时,加权系数全部为1,利用最小二乘法对6个未知参数进行求解。
1.2.2 先验估计
由于基本约束方程中的假设,光流法在大位移情况时会估计失败[12]。为了解决该问题,有学者在Lucas-Kanade光流法的基础上利用金字塔分层技术[18-19]来求解位移。首先把数据进行金字塔分层,从最顶层开始求解光流,将其结果作为下一层的初始值,重复上述过程直至最底层,这种由粗到细的方法很好地将大位移分解成小位移。
有些学者在仿射变换的基础上进行组织的运动估计,如LIU等[15]用Powell方法迭代求出位移和应变;MERCURE等[16]基于拉格朗日斑点模型,利用Levenberg-Marquardt方法迭代求解,实现无创血管超声弹性成像;PAN等[17]提出了两步光流法可同时得到位移和应变信息。
然而,由于原始射频回波信号的数据量大,上述方法的实时性都不高。该研究采用了先验估计的思想,利用相邻点已知位移作为当前点位移估计的先验值[13],缩小搜索范围,既满足了光流法的小位移条件下的假设,又大大提高成像速度。但由于算法中存在窗移,因此需要对位移和应变数据进行二维线性插值。算法流程如图1所示。
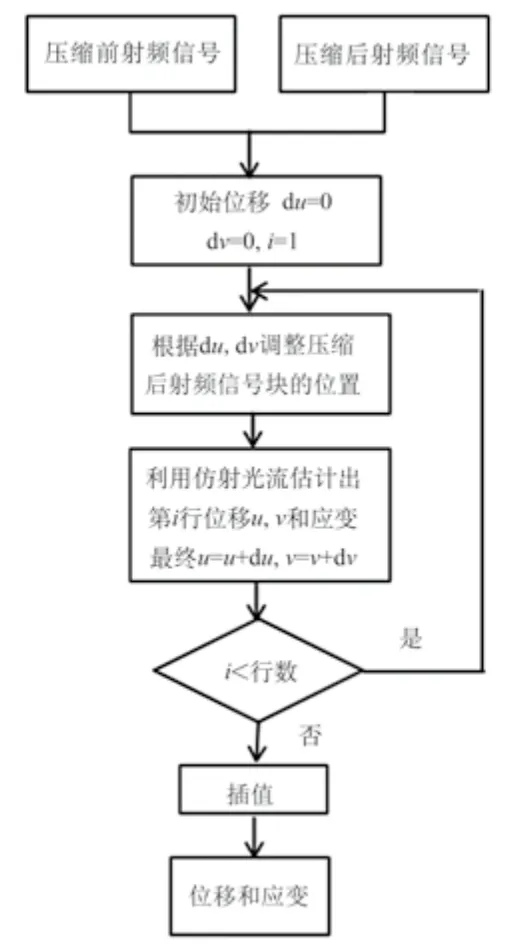
图1 算法流程图Fig.1 The flow diagram of algorithm
为了方便定量分析,新提出的算法与一种局部图像形变算法[20]的成像质量进行对比。对比算法首先用块匹配法获得初始整数位移,然后假设组织局部形变为仿射变换,利用光流法对初始位移进行修正。
1.3 评价指标
本文主要从应变成像质量和算法速度两方面对算法性能进行评价。通常利用信噪比(SNRe)和对比度噪声比(CNRe)来评价应变图像质量和病灶的检测能力[15,17,21],用时长来评价算法速度。
SNRe定义为:

其中,es和σs是在均匀弹性模量区域的平均值和标准差,在该文中均匀弹性模量区域有嵌入物目标区和背景区。除了SNRe外,CNRe也常用于在弹性成像中, CNRe的值越高表示检测病变的能力越好。
CNRe定义为:
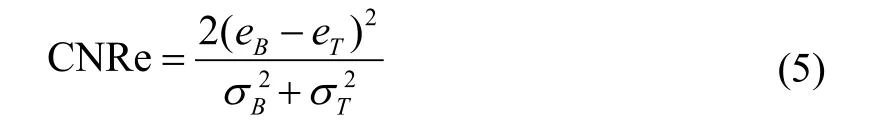
其中,eB和σB别是背景区域的均值和标准差, eT和σT是目标区域的均值和标准差。
1.4 仿真实验
利用Comsol Multiphysics5.2软件构建一个大小为100 mm×10 mm×50 mm的三维模型,中心处有一个半径为5 mm的球,球形区域的弹性模量为基质区域的10倍,泊松比为0. 495。由于压缩量过大没有实际应用意义,所以本文仿真了2%,5%,8%三种压缩量的数据。设置边界条件,上表面分别指定位移为-1 mm、-2.5 mm和-4 mm,即代表压缩量为2%、5%和8%,下表面固定,其他表面为自由边界条件。FieldⅡ模拟超声场,获取压缩前后的射频回波数据。仿真数据的中心频率为7.5 MHz,采样频率为100 MHz,散射点个数为50 000,最终的仿真数据大小为6 501×449。信号保存之后在MatLab离线处理。本研究只对比两种算法的轴向运动,即沿着超声探头发射方向。
2 结果
在MatLab平台上用仿真射频回波数据对两种算法进行实验,其中本研究算法中的窗口大小为3.08 mm×2.87 mm,窗口之间的重叠率为63%。从图2和图3中可以看出,在2%和5%压缩量下两种算法估计的位移和应变差别不太明显。在8%压缩量情况下,如图4(c)所示,对比算法得到的位移图中间部分出现大的噪声斑块;应变图中间硬物部分整体边界不规则,背景区域噪声过多,整体位移和应变成像质量差。从图2,图3和图4无法直接得到应变图成像质量的好坏,因此,需要对两种算法估计得到的应变图成像质量进行定量分析,结果如表1所示。
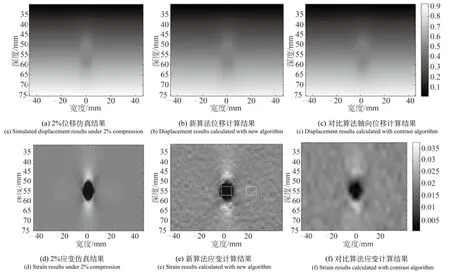
图2 2%位移和应变计算结果Fig.2 Displacement and strain calculated results at 2%

图3 5%位移和应变计算结果Fig.3 Displacement and strain calculated results at 5%

图4 8%位移和应变计算结果Fig.4 Displacement and strain calculated results at 8%
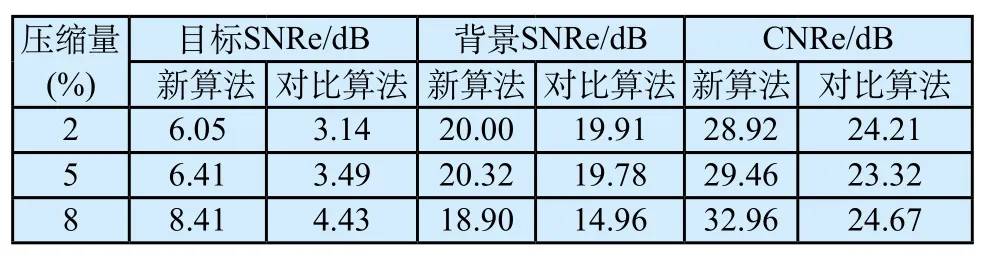
表1 信噪比和对比度噪声比结果Tab.1 The result of SNRe and CNRe
计算信噪比和对比度噪声比时,在应变图的目标区域和背景区域选取两个等大矩形,如图2(e)所示,大小为4.61 mm×8.00 mm,定量指标结果如表1所示。在2%和5%压缩量时,新提出的算法估计得到的应变图在目标区域的信噪比和对比度信噪比都高于引用算法,但两种算法的背景区域的信噪比相差不大,说明在小应变情况下,虽然两种算法对病灶的检测能力不同,但应变图的背景区域成像质量相差不大。在8%压缩量时,新提出的算法应变图定量指标明显优于对比算法,其中目标区域的信噪比高出3.98 dB,背景区域的信噪比高出3.94 dB,表明该研究算法在8%大压缩量下应变成像质量较好;对比度噪声比高8.29 dB,说明本研究算法对病灶的检测能力较强。对比上述结果,说明本文算法可以在大压缩量情况下相对准确地估计出轴向位移和应变结果。
在相同的计算环境下(Dell,内存8 GB,处理器Inter(R) Xeon(R)CPU E5-2665 0 @2. 40 GHz 2.40 型号PrecisionT7600)对两种算法进行实验,随着压缩量的增加,对比算法的计算时间明显增加,如表2所示,主要由于对比算法中第一步利用块匹配来估计整数位移,当压缩量增加时,为了相对准确地估计出初始位移,块匹配搜索参数也要增大,所以对比算法在未知压缩量情况下使用时存在劣势。本文算法计算时间基本稳定在8.3 s左右,其远远小于引用算法,因此,本文算法在实时显示上更有优势。

表2 两种算法在不同压缩量下的时长Tab.2 The time of two algorithm under different compression
3 总结
本文阐述了一种基于仿射变换的光流超声弹性成像算法,引用了先验估计的思想,不仅克服了光流法只能进行小位移估计的缺点,而且削弱了基于位移梯度的算法中由于模型不精确造成位移估计误差,同时估计出位移和应变信息。仿真实验证明,本研究算法在大压缩量情况时,应变图信噪比、对比度噪声比和算法时长与对比算法相比都有明显提升,对实时超声弹性成像的应用有良好的推进作用。

