纵向增强体新型土石坝稳定性研究

侯奇东， 梁 军， 李海波， 戚顺超

(1. 四川大学 水力学与山区河流开发保护国家重点实验室， 四川 成都 610065；2.四川省水利厅， 四川 成都 610016； 3.四川大学 水利水电学院， 四川 成都 610065)

1 研究背景

土石坝因其对地质地形条件适应性强、坝体材料可从当地获取，以及施工方法成熟等优点，在国内外受到广泛应用[1]。图1展示了世界范围及四川省内的坝型及规模统计。国际大坝委员会针对全世界59071座典型大坝的统计数据显示，土石坝占比达到65%。我国西南地区地质条件复杂，且受到地震影响，建坝条件差，土石坝则更加受到学者们的关注。四川省水利普查公报显示，截至2013年，四川省土坝数量占比达88%。事实上，土坝只是土石坝的一种，若将堆石坝、浆砌石坝也计入土石坝范畴，其占比将更高。由此可见，土石坝应用的广泛程度及其对社会经济的影响程度远非其他坝型可比。我国已建大坝以小型坝为主，统计显示，四川省小型坝占比超过96%。综上所言，在我国西南地区，绝大多数大坝为小型土石坝，其安全与稳定举足轻重。

另一方面，此类小型土石坝多建于20世纪60、70年代，受当时经济技术条件不完善的制约，现如今不少坝体存在渗漏、开裂、滑坡、白蚁侵蚀等隐患[2]。因此，改造和维护工作势在必行。然而大坝数量颇多，维护工作繁琐且难以开展，若拆除重建，造价与工期又大大增加。

针对上述问题，相关学者提出了一种新型土石坝的修建思路：先整体填筑坝体，随后中间掏槽浇筑混凝土心墙作为防渗体，谓之纵向增强体土石坝[3]。图2展示了纵向增强体土石坝设计原理。所谓纵向增强体，指的是作为刚性结构体的混凝土心墙，其贯穿整个土石坝坝体中部，底部插入基岩并结合帷幕灌浆达到防渗目的。为缓解变形不协调问题，在坝壳料与心墙之间设置过渡料，如图2所示。此新坝型的最大创新之处在于将防渗墙技术运用于整个坝体，并通过理论研究将刚性防渗墙从单一的防渗体上升为可抵抗变形的结构体[4]，从而带来土石坝防渗技术、施工方法与安全性能的变革。

据此方法，对于有隐患须改造的土石坝，无须拆除原坝体，直接在老坝基础上加固或加高，随后再掏槽浇筑混凝土心墙，则效率提升，事半功倍。再者，纵向增强体土石坝施工工艺简单、工序简捷，坝体填筑不受心墙施工的影响，施工速度更快。在坝区无满足要求的黏土心墙料，且工期紧、投资省的情况下，新坝型具有推广意义。综上，相对于传统黏土心墙坝，以及工艺繁复容易因控制不当而出现变形开裂、水力劈裂的沥青混凝土心墙坝[4-5]，纵向增强体土石坝都更具优势。

位于四川省通江县的方田坝水库是国内首例采用纵向增强体土石坝的工程，目前已竣工，也有相关的设计总结[6]，但均属初步研究。对于这一没有采用传统黏土心墙的土石坝，其防渗效果也尚未得到实际蓄水的检验。而在柔性坝壳料中插入刚性心墙这一思路，必然带来不可忽视的变形协调性问题，进而可能诱发心墙开裂的不利情况；另外，此新型土石坝抵抗水力劈裂的能力也缺乏相关研究。因此，新坝型的合理性亟需相关科研和工程人员的深入探讨。针对以上问题，本文将基于方田坝水库实例，采用数值模拟方法，对纵向增强体新型土石坝的稳定性展开研究；同时，由于新坝型的坝坡坡比缺乏相关设计规范和相似的工程可借鉴，本文也将对其可优化性展开讨论。

2 方田坝水库工程概况

方田坝水库位于小通江河右岸一级支流冯家沟上游河段，坝址位于通江县民胜镇方山村境内，距通江县城约8.0 km。工程原为小(2)型水库，大坝为粘土心墙坝，坝顶高程556.60 m，坝高约15 m。后根据相关规划、水库建设条件以及周边综合利用要求，将其扩建为具有城乡供水、农业灌溉等综合利用功能，并作为抗旱应急水源的小(1)型水库。水库大坝在原大坝基础之上加高，采用C25刚性混凝土作为防渗心墙。

扩建后大坝正常蓄水位577.50 m，坝顶高程581.00 m，坝顶宽6.0 m，坝顶轴线长365.00 m，最大坝高41.50 m。混凝土心墙位于坝体中部偏上游1.5 m，心墙厚0.80 m。施工时，大坝先整体填筑坝壳料至575.00 m高程，利用该高程上宽为31.50 m平台作为混凝土心墙的施工平台，然后通过中间掏槽、泥浆固壁的工艺浇筑防渗心墙。575.00 m高程至坝顶采用现浇混凝土心墙，两种施工方式的心墙之间采用钢筋连接。

3 纵向增强体新型土石坝稳定性计算

3.1 分阶段建模

选取方田坝水库大坝的典型横断面进行建模时，为使结果更客观，充分考虑到现场施工次序，分为5个阶段，分别为：尚未填筑、填筑至575 m高程、混凝土心墙掏槽浇筑、坝体填筑至坝顶、蓄水，如图3所示。随后即采用Phase2软件对坝体及心墙的安全性进行有限元(Finite Element Method)分析。模型采用3节点的三角形单元，并设置为变密度网格，总节点数为9 578，总单元数为1 8174。坝体表面为自由边界，左右两侧约束水平方向，底部约束水平及竖直方向。坝体各部分材料基于摩尔-库仑理论的计算参数见表1。需要注意的是，强度参数在蓄水后有一定的折减。相关学者已对岩石浸水后强度降低的性能，也即岩石的软化性进行了研究，并且指出吸水能力强的岩石受水的侵蚀作用更大[7-8]。另一方面，坝体堆石料为散粒体结构，若将其看作非饱和土体，根据非饱和土力学，其抗剪强度也会随含水率上升而下降[9]。

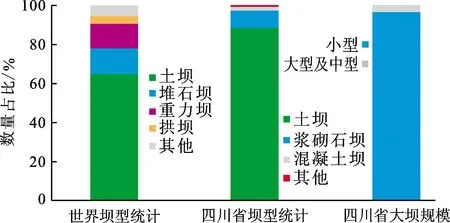
图1 世界及四川省内坝型及规模统计

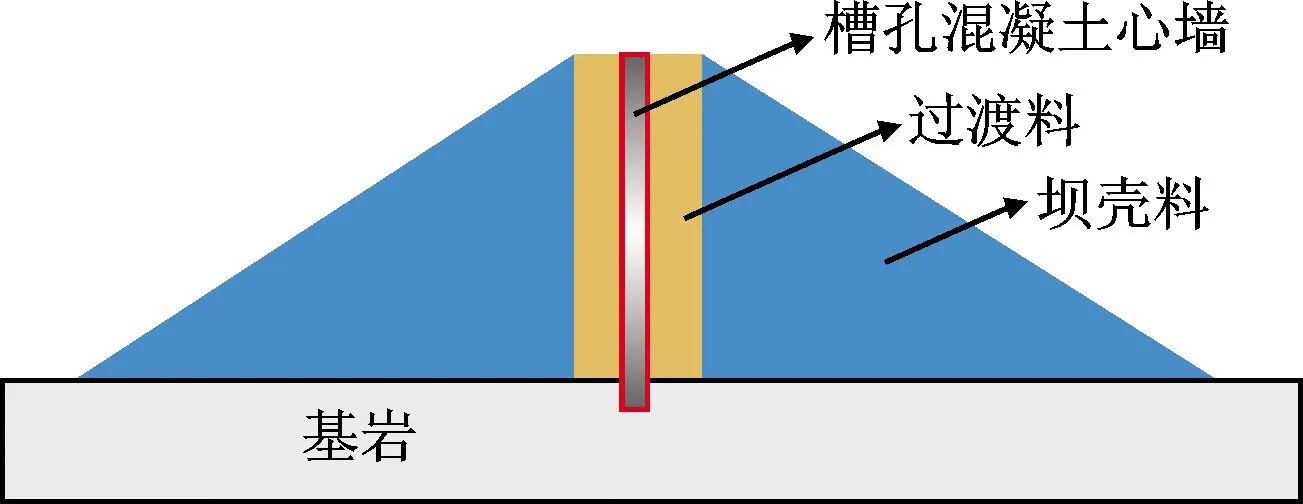
图2 纵向增强体土石坝设计原理

在依托上述理论的基础上，结合现场工程经验，本文计算有水作用时，砂泥岩堆石料的折减系数为0.8，其余受水影响的坝体材料的折减系数为0.9，基岩、混凝土心墙以及未接触水的坝体材料不折减。

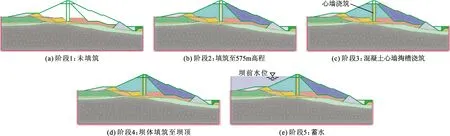
图3 坝体分阶段建模

3.2 渗流稳定分析

对于土石坝而言，良好的防渗效果是其维持稳定和发挥功用的前提，因此渗流稳定也是最核心的问题。方田坝的渗流模拟结果如图4所示。其中，右上角的空白部分表示负孔隙水压力，可以理解为基质吸力[10-11]，也即右上角土体处于非饱和状态，位于自由水面以上。显然，坝体孔隙水压力分布呈现出与传统土石坝显著不同的特征：坝体浸润线在心墙处急剧下降。混凝土心墙虽只有80 cm厚，但因其渗透系数极小，几乎不透水，浸润线直接从上游水位下降至心墙底部约539.00 m高程处。此后浸润线近似水平，直接经堆石排水带和堆石棱体进入下游。

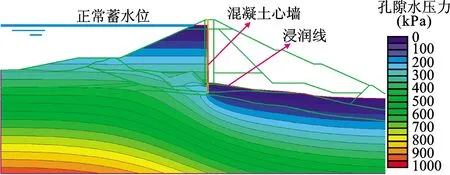
图4 坝体孔隙水压力模拟云图

由此可见，混凝土心墙的防渗效果极佳，下游坝壳料几乎免受渗透水流的作用，从而规避了困扰传统土石坝的流土、管涌等渗透破坏问题，也为工程的顺利运行奠定基础。

3.3 心墙结构稳定分析

纵向增强体土石坝的最大创新之处在于扬弃了黏土防渗心墙，在坝体填筑完成后通过掏槽浇筑混凝土心墙防渗。上节的计算结果已经表明，新坝型的防渗效果是不足为虑的。其真正的问题在于：混凝土材质的心墙在杨氏模量上与两侧堆石体差异颇大，超过两三个数量级，坝体在沉降过程中，必然会有变形不协调的问题；同时蓄水期在上游静水压力的推动下，心墙难免会产生挠曲。然而混凝土材料抗压不抗拉，一旦心墙因变形产生拉应力超过其抗拉强度，进而产生裂缝，则防渗效果陡降，大坝安全风险剧增。

计算完成后，本文选取心墙中心轴进行变形分析。参考3.1节的分阶段建模可知，心墙在第3阶段完成浇筑(图3(c))，则心墙变形分析应以第3阶段为基准计算相对变形。结果显示，心墙沉降值很小，在1 cm左右，研究的重点应是水平变形。图5清晰地显示了心墙水平变形随着蓄水水位抬升的变化规律：竣工期几乎无变形，蓄水后在静水压力的推动下，同时受到底部基岩、两侧土压力的作用，呈现出从底部到顶部逐渐增加的“J”型的挠曲；同时随着蓄水水位的抬升，水平变形略有增加。

显然，混凝土心墙在蓄水后出现了挠曲变形，上下游边界可能出现拉应力。为验证猜想，在此分别选取了心墙上、下游边界的大、小主应力进行分析，如图6所示(图中以压应力为正，拉应力为负)。最大压应力体现在大主应力中，而拉应力则体现在小主应力中。分析主应力可知，最大压应力出现在心墙上游边界约541 m高程处，蓄水后在水压力影响下明显增大，且随蓄水水位的抬升而缓慢增加，校核洪水位时达到最大值3 340 kPa，但仍不足以对心墙结构产生威胁。而拉应力仅出现在心墙下游边界，并且随着蓄水水位的抬升，拉应力有所增大。最大拉应力出现在539.5 m高程，校核洪水位工况时达到最大值-174.01 kPa。最大压应力与拉应力几乎出现在同一高程，正好验证了图5中的心墙变形规律，即心墙的“J”型挠曲导致下游出现拉应力。不过，拉应力尚小，在可控范围内；且拉应力出现位置在填筑料底部，即使此处防渗效果骤减，对于大坝整体防渗效果的影响也有限。

图7展示了混凝土心墙的拉应力出现位置及其受力变形特性。进一步观察可知，拉应力最大值出现在心墙下游断面覆盖层与过渡料的分界处。对于这一规律，本文提出4点原因：

(1)心墙底部插入基岩，近似于固定端，几乎无变形；

(2)静水压力随水深增加而增加，因此心墙下部出现较大弯曲，上部近似竖直；

(3)上、下游两侧土压力对心墙中上部变形的限制作用；

(4)覆盖层与过渡料弹性模量差异较大，心墙在分界处上下发生变形的容易程度不同。

在上述4个影响因素的综合作用下，心墙下游会出现一个拉应力危险点(图7中已标出)。然而，数值模拟的结果表明水平总变形较小(图5)，变形所致的心墙拉应力不足以威胁坝体结构。其中，心墙两侧土压力的作用对于维持变形不至于过大最为关键。在竣工期心墙几乎没有水平变形，因此，两侧堆石体施加的力可以看作静止土压力。蓄水后，心墙向下游变形，上游堆石体作用转化为主动土压力，下游则转化为被动土压力[12](图7)。此时被动土压力的量值大于主动土压力，且被动土压力随着墙体向下游位移的增大会继续增大[13-15]，如图8中墙体位移与土压力的关系曲线所示。这一规律很好地限制了混凝土心墙的水平变形，也将心墙下游出现的拉应力控制在可接受的范围。

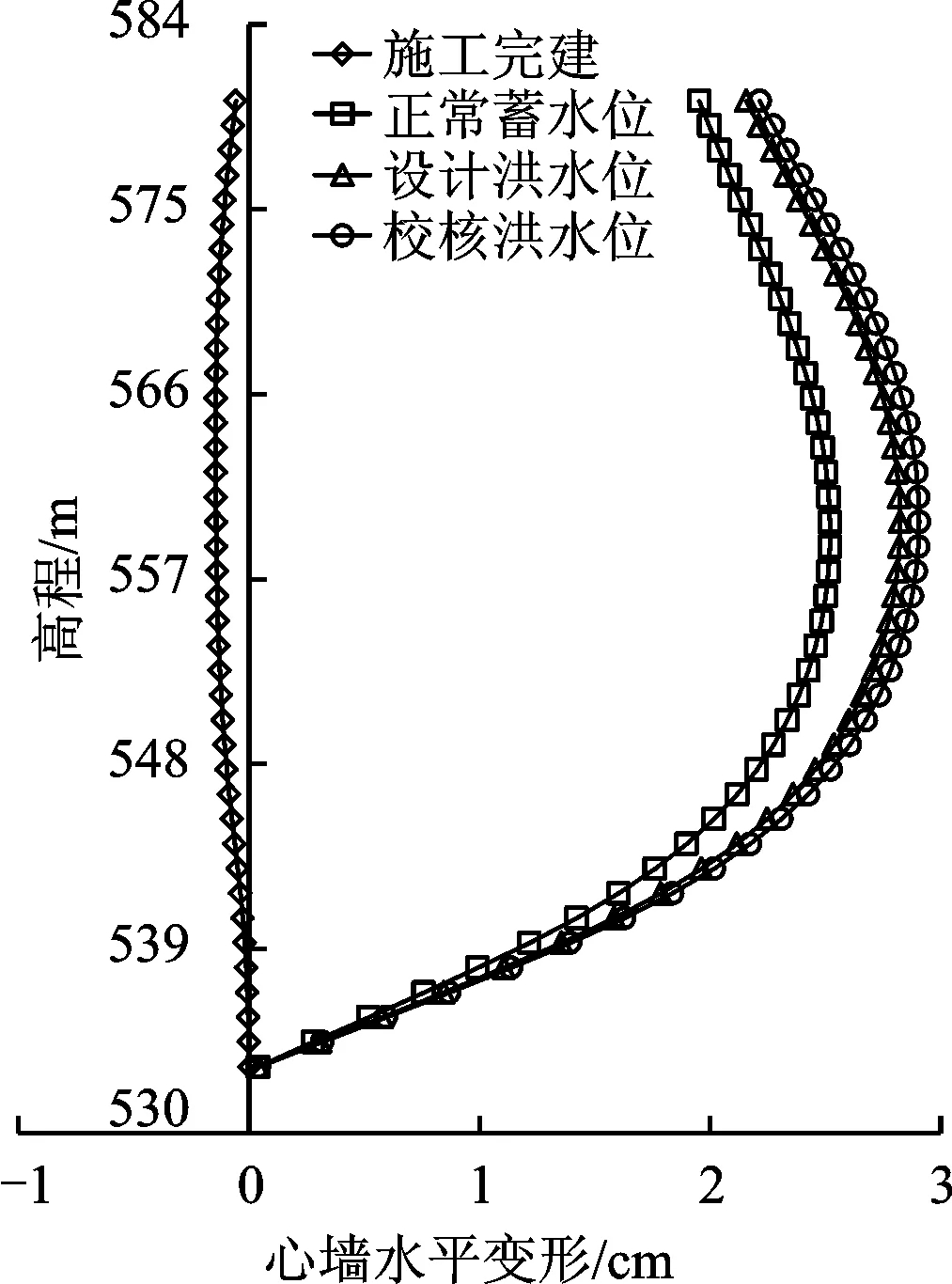
图5 蓄水后不同蓄水位心墙水平变形随高程的变化

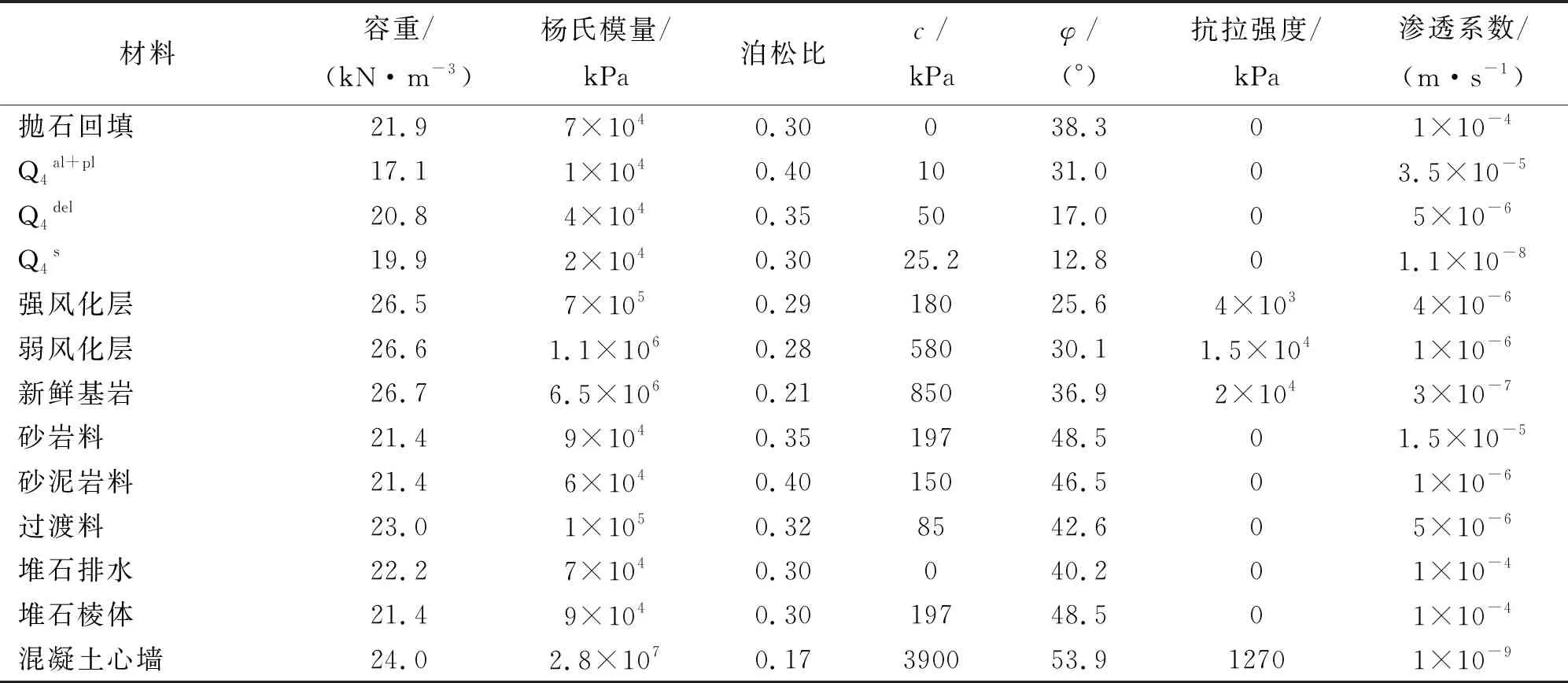
表1 坝体各部分材料计算参数取值

注：Q4al+pl为冲积洪积堆积层； Q4del为地滑堆积层； Q4s为人工堆积层。

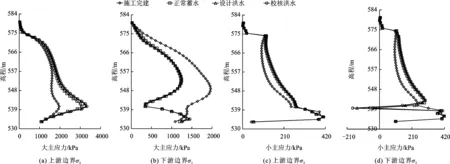
图6 不同蓄水位心墙上、下游边界大、小主应力随高程变化

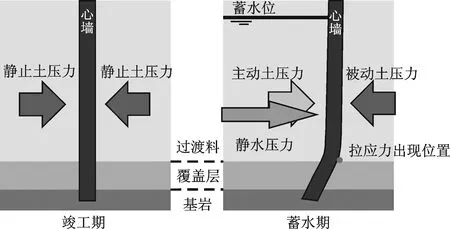
图7 蓄水期心墙结构稳定分析

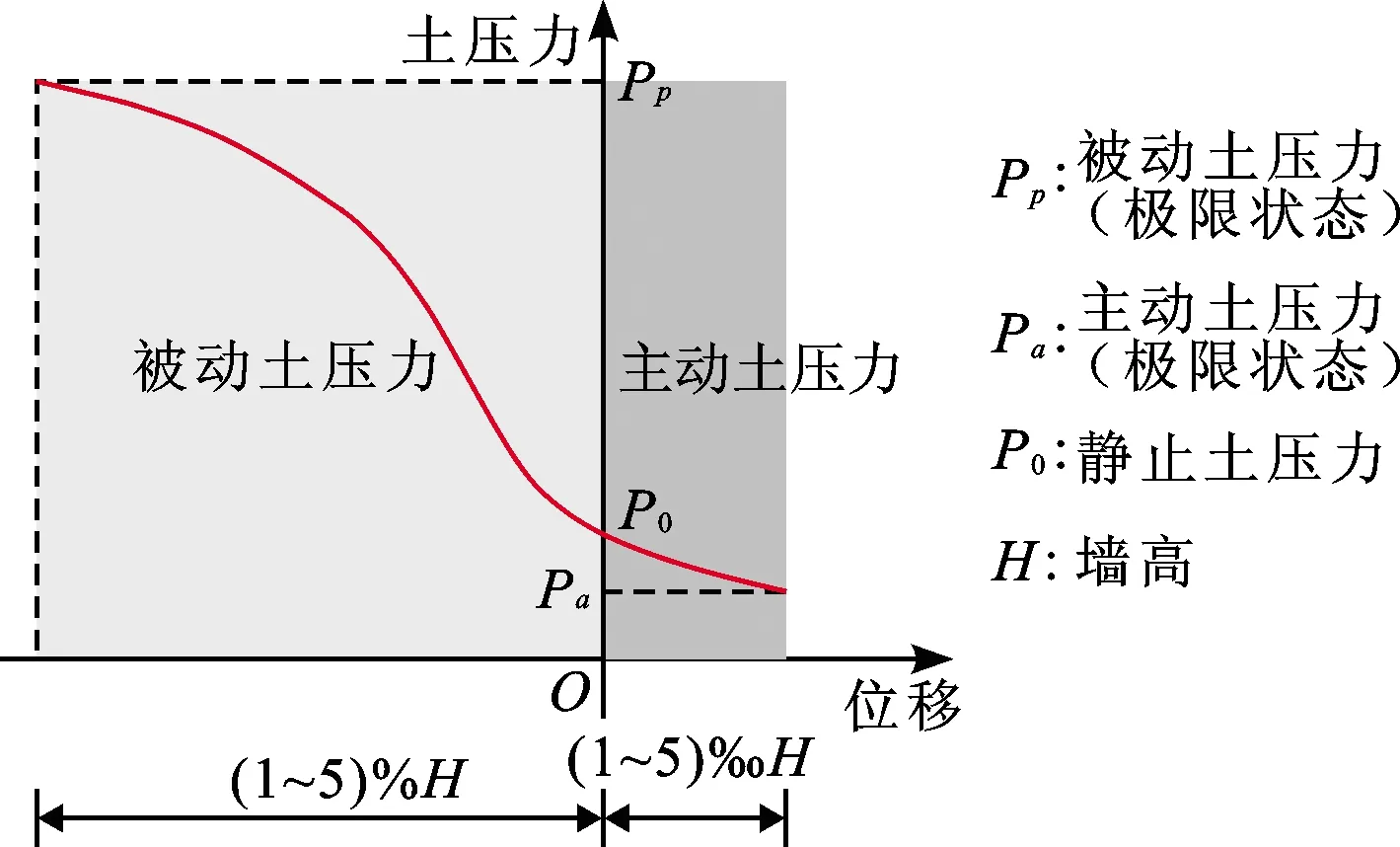
图8 墙体位移与土压力关系曲线

3.4 水力劈裂风险分析

对于传统土石坝而言，水力劈裂问题是一重大隐患。同时，传统黏土心墙与坝壳料之间也存在变形协调问题，若坝壳料沉降完成后心墙仍在沉降，坝壳料就会支撑心墙产生“拱效应”，加剧水力劈裂的风险[16]。简而言之，水力劈裂就是水压力超过土体中的应力而将土体劈开的现象[17]。因此，众多水力劈裂的判定准则都是基于水压力与土中应力的关系而得。这样的判定方法对于黏土心墙适用，对于混凝土心墙却相差甚远。原因在于：与黏土相比，混凝土材质的心墙是具有抗拉强度的。因此，本文采用黄文熙[18]提出的判定准则：如果心墙某点上的竖直方向主应力(σy)与土的抗拉强度之和小于该点处的孔隙水压力，心墙就会因水力劈裂产生裂缝。采用此方法，在正常蓄水位下的计算结果如图9所示。图9还简明表示了心墙水力劈裂的过程。显然，孔隙水压力远小于竖直方向主应力σy与心墙抗拉强度之和，也即孔隙水压力不足以沿垂直于σy的方向“劈开”心墙，如图9所示。因此，混凝土心墙在抵抗水力劈裂方面有显著优势。在坝高较小时，蓄水水位不足以提供过大的孔隙水压力，从而几乎免除了水力劈裂的风险。

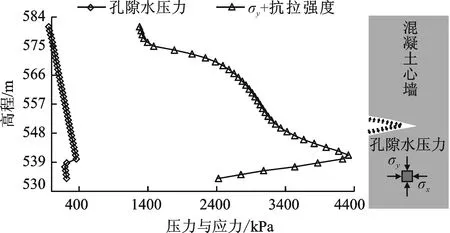
图9 水力劈裂风险分析

4 纵向增强体新坝型坝坡坡比可优化性探讨

4.1 工况设置

通过上节的数值模拟结果可知，基于方田坝工程所建立的实例模型安全稳定性良好。但作为纵向增强体新型土石坝，其坝坡坡比是否可以优化，即是否可采用更陡的坝坡比，从而节省建筑材料、提高施工效率还不明确，也没有相关规范和相似工程可借鉴。因此，在方田坝水库大坝模型的基础上，本节将分4种工况对纵向增强体土石坝的最优坝坡坡比展开探讨。具体工况设置见表2。其中，工况0即为方田坝工程实际的坝坡坡比，其作为一个参照工况参与分析。其余3种工况即在工况0的基础上改变坝坡坡比所得，坝高以及坝体材料等均保持一致，计算模型参见图10。

表2 工况设置

注：工况0中，下游坝坡坡比在第1级马道以上为1∶2，之下为1∶2.25。

4.2 坝坡稳定性对比

坝坡变陡后，首先考虑到坝坡作为一种土质边坡，其安全性必然变差。而坝坡稳定是土石坝整体结构稳定的基础，稳定的坝坡是土石坝坝体牢固屹立于河道之中的保证。因此，本节依托Flac3D软件，通过有限差分法(Finite Difference Method)，并按照强度折减法计算坝坡的安全系数[19]。在每一种工况下，分别考虑竣工期、正常蓄水以及水位骤降下的安全系数。其中水位骤降为假想状态：即上游水位从正常蓄水位577.5 m骤降至564.4 m，上游坝坡内水位来不及下降，坝坡内和坝坡外形成水位差。在水库的运行过程中，这一状态是有可能存在的。进行坝坡稳定分析时，为简化计算，假定心墙结构稳定，足以发挥正常防渗作用。

计算过程中可以发现，上游覆盖层相对较厚，以致施工完建后上游沉降较多，因此竣工期上游坝坡相对更危险；而蓄水后，尽管上游坝体材料的强度参数会因浸泡有所软化，但孔隙水压力的作用有利于其保持稳定[20]，下游坝坡却由于静水压力的推动而更为危险；当发生水位骤降时，坝坡内和坝坡外形成水位差，产生指向坝坡外的渗流，因此上游坝坡安全形势恶化[21-23]。安全系数的计算结果见表3，其数值为分别计算各工况上下游坝坡后得出的最不利值。因此，竣工期和水位骤降状态下展示的是上游坝坡的安全系数，而正常蓄水时则为下游坝坡的安全系数。显然，坝坡安全系数随坡度变陡而减小，并且水位骤降为坝坡稳定最不利的状态。最大剪应变增量可以反映出潜在滑动面的位置[24]。图10展示了各工况在水位骤降时的最大剪应变增量，由图10可以发现，随着坝坡逐渐变陡，潜在滑动面逐渐贯通，安全系数自然随之减小，工况3时安全系数达到最小值1.48(表3)。

4.3 心墙结构稳定性对比

坝坡坡比改变后，除了坝坡自身的稳定性，另一个亟需关注的问题是心墙的结构稳定性。上节的分析结果表明：心墙之所以能维持相对较小的变形和可接受范围内的拉应力，是由于下游堆石体被动土压力的限制。而当坝坡坡比改变后，下游堆石体的形态和质量都发生了改变，心墙的结构稳定性有待验证。同样采用有限元法对比分析后，得出正常蓄水位下，心墙水平变形结果如图11所示：显然，坝坡越陡，蓄水后心墙水平变形越大，且增长趋势显著，无收敛迹象。结合上节对于心墙水平变形的分析，即可得出推论：坝高及蓄水水位一定时，下游坝坡越陡，心墙在上游水压力推动下发生相同的水平位移时，受到的被动土压力越小。换言之，坝坡越陡，心墙的结构稳定性越得不到保证。同时可见，坝坡越陡，心墙挠曲变形的曲率越大，心墙内应力的波动也更大。通过上节的分析已知：心墙拉应力会出现在下游边界。因此，选取4种工况下心墙下游边界的小主应力进行对比，结果如图12所示。由图12可看出，最大拉应力出现在同一高程(539.5 m高程)，且随坝坡变陡而逐渐增大。坝坡变陡带来的增大效应显著，工况1相对于工况0拉应力增长了4.2倍，工况2相对于工况1增长了1.3倍，工况3相对于工况2增长了0.6倍。当坝坡坡比升至1∶1.5时，最大拉应力已经达到-877.7 kPa。

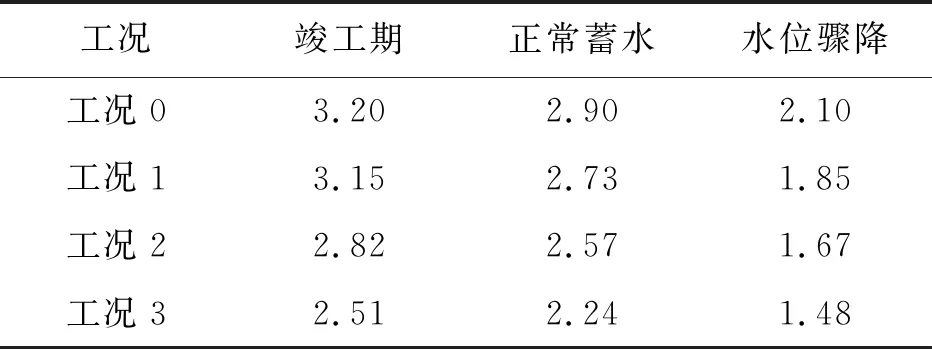
表3 各工况不同状态下坝坡安全系数

4.4 可优化性探讨

根据碾压式土石坝设计规范[25]，方田坝作为小(1)型水库，坝坡安全系数不应小于1.25。规范中的安全系数虽是依据极限平衡法所得，但有学者指出其数值与按强度折减法所得之值相差不大[26]，因此可作为参考。由于表3中的安全系数均大于规定的最小值，所以坝坡稳定性在各工况下都可以得到保证。另一方面，心墙下游边界拉应力随坝坡变陡而逐渐增大，工况3时达到最大值-877.7 kPa。坝坡变陡后拉应力增长虽快，但其值仍在可接受的范围内，且均只出现在填筑料底部，对坝体威胁有限。综上所述，数值模拟的结果表明，坝坡优化、坡度变陡在理论上是可行的。

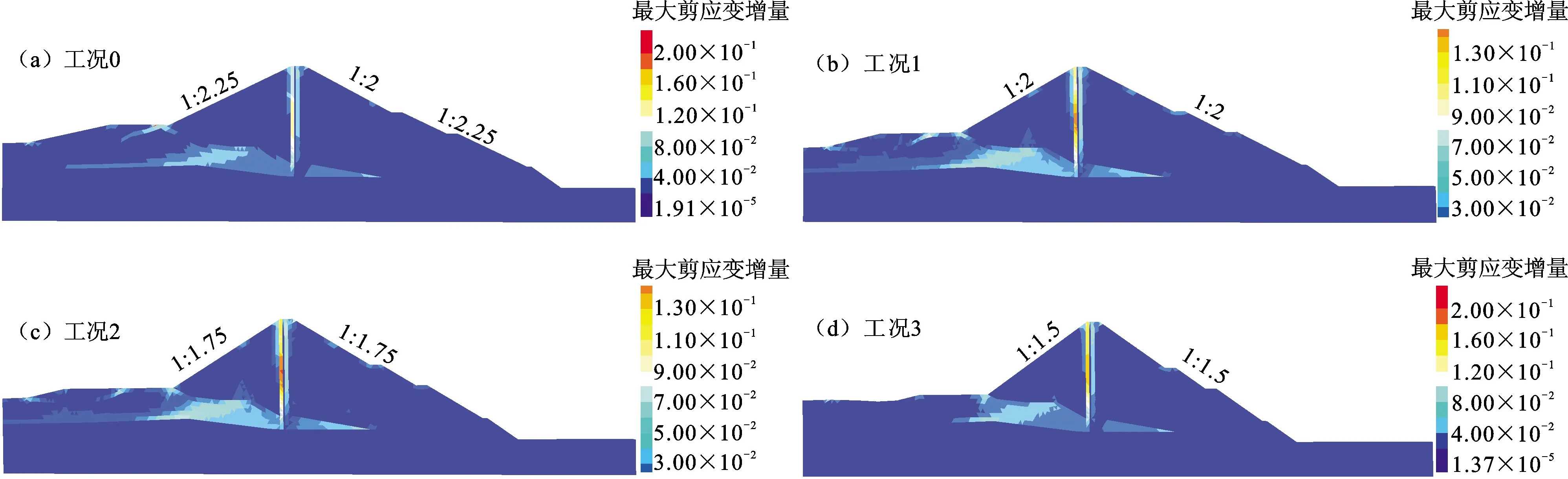
图10 水位骤降时各工况坝体最大剪应变增量云图

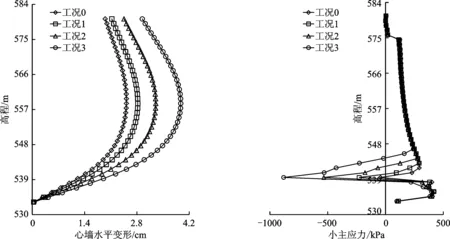
图11不同工况下的心墙水平变形 图12不同工况下心墙拉应力垂向分布

然而，在复杂的自然环境下，实际运行过程中必然存在大量威胁大坝稳定的不确定性因素，而坝坡变陡带来的心墙拉应力快速增长可能孕育更多的潜在威胁，这些都难以通过计算机准确而全面地模拟。纵向增强体土石坝作为一种新坝型，工程经验极其缺乏，又没有相关的监测数据可借鉴。其坝坡能否真正维持稳固、心墙能否保证不开裂，都有待方田坝水库实际蓄水运行的检验。因此，方田坝水库作为开拓性的首例采用新坝型的工程，并未选择坝坡优化、坡度变陡，而是选择了一种更为稳妥的方案，从而留有足够的安全储备。不过随着土石坝理论和工程技术的发展，新坝型因其工序省、效率高等优点必然会得到推广。而随之获取的丰富监测数据以及积累的新坝型工程经验，将使得坝坡比的优化真正得到应用。

5 结 论

本文基于方田坝水库工程实例，结合数值模拟方法，对混凝土心墙纵向增强体新型土石坝的稳定性展开了研究，并对新坝型坝坡比的优化展开了探讨。研究结果表明：

(1)混凝土心墙的防渗效果显著，下游坝壳料几乎免受渗透水流的作用，从而在一定程度上规避了困扰传统土石坝的流土、管涌等渗透破坏问题；

(2)蓄水后在静水压力、土压力、底部基岩和覆盖层的综合影响下，心墙呈现“J”型挠曲，从而在下游边界产生拉应力。但拉应力尚小，在可控范围内；且拉应力出现位置在填筑料底部，即使此处出现裂缝，大坝整体防渗效果遭到破坏性影响的可能性也较小；

(3)混凝土心墙在抵抗水力劈裂方面有显著优势，在坝高较小时，很大程度上减缓了水力劈裂的风险；

(4)坝坡优化、坡度变陡在理论上虽然可行，但需要经过长时间工程实践的检验。因此，方田坝水库作为首例采用新坝型的工程，为稳妥起见并未优化坝坡。随着经验积累和技术提升，新坝型坝坡的优化有机会在将来得到应用。

综上所述，在坝高较小，且维持合理而安全的坝坡坡比，并保证施工质量的前提下，纵向增强体土石坝具有相对较好的稳定性。