径流序列变异诊断的近似熵与样本熵法对比研究——以新疆叶尔羌河为例

薛嵩嵩， 高 凡， 何 兵

(1.新疆农业大学 水利与土木工程学院， 新疆 乌鲁木齐 830052 ；2.西安理工大学 省部共建西北旱区生态水利国家重点实验室， 陕西 西安 710048)

1 研究背景

河川径流是水文循环的基本环节，可以直接反映气候变化和人类活动对水文循环的影响[1]。受变化环境影响，径流序列若发生变异将导致水文资料一致性破坏，不利于水文分析与模拟及水资源规划与利用工作。识别径流序列变异点是进行径流序列重构与一致性再建立的关键技术环节，对于认知变化环境下水文序列形成、演变及响应机理和应对径流变化进行水资源适应性管理具有重要意义[2]。传统的水文数理统计方法，如Mann-Kendall法，滑动T检验，滑动F检验，贝叶斯变点分析法，pettitt检验法等，多倾向于识别径流序列的突变点。如祁文燕等[3]采用Mann-Kendall法对湟水干流近60年径流进行突变特征分析；陈立华等[4]采用有序聚类法和滑动T检验法对西江干流近60年径流资料进行突变分析；王琪森等[5]采用时序累计值相关曲线法识别南四湖流域突变点。黄强等[6]认为，突变点不等同于变异点。由于传统的径流序列突变点诊断方法对参考数据序列长度要求严格和对噪声有较强敏感性等特点，应用于非线性、非稳定性的径流时间序列变异点诊断尚存在一定的局限性。伴随非线性理论的发展和不断完善，Pincus于1991年提出近似熵(ApEn)法，以其较强抗干扰抗噪能力、所需数据序列短、能获得稳定的计算成果等优势得到广泛应用[7-8]。在近似熵法基础上，2000年Richman和Moorman提出一种新的时间序列复杂性度量方法——样本熵法，该方法是近似熵的改进算法，能更好地维持计算结果的一致性[9]。

叶尔羌河流域是塔里木河流域四源一干水系格局的重要组成部分，叶尔羌河径流序列变化直接关系到塔里木河流域水生态安全和水资源开发利用。变化环境下，叶尔羌河流域气温、降水序列演变特征与新疆气候变化趋势一致，即呈暖湿化发展[10]，在此背景下叶尔羌河径流序列演变响应及变异点诊断研究成果较少。本文分别采用近似熵法和样本熵法对叶尔羌河源流区卡群水文站1957-2016年60 a的日径流序列进行变异诊断，并对比分析两种方法变异诊断效果，以期为气候变化和人类活动影响下干旱区内陆河流水文过程演变以及水资源的适应性管理研究提供科学决策支持。

2 研究区概况

叶尔羌河流域东依塔克拉玛干大沙漠，西接布古里、托格拉克沙漠，南以喀喇昆仑山为屏障，北与天山南麓余脉相毗邻，流域总面积8.57×104km2, 位于74°28′～80°54′E、34°50′～40°31′N[11]。叶尔羌河是喀什地区第一大河流，也是塔里木河的主要源流之一，发源于喀喇昆仑山北坡的拉斯开木河，全长1 179 km，多年平均年径流量65.45×108m3[12]。

图1 研究区示意图

3 数据来源与研究方法

3.1 数据来源

卡群水文站(海拔1 450 m)位于76°54′E、37°59′N，是叶尔羌河总水量控制站，多年平均径流量为68.75×108m3，其中，冰雪融水占70%左右[13]。本文采用叶尔羌河源流区卡群水文站1957-2016年60 a实测日径流数据序列，并收集同期气温和降水数据序列。数据资料均来源于新疆水文年鉴及叶尔羌河流域水文水资源局。

3.2 研究方法

本文采用累积距平法[14]分析研究区年径流序列的趋势性变化特征，采用突变检验法——Mann-Kendall法[15]识别径流序列的突变点。分别运用近似熵法和样本熵法诊断长系列日径流序列的变异点并进行方法对比，限于篇幅关系，本文仅介绍近似熵法与样本熵法，累积距平法、Mann-Kendall检验法详见参考文献[14-16]。

3.2.1 近似熵方法 近似熵(ApEn)法由Pincus于1991年提出，该方法基于时间序列复杂性角度度量信号中产生新模式概率的大小，即时间序列在模式上的自相似程度[17]。其值越大，表明产生新模式的概率越大，即时间序列的复杂程度越高[18]，复杂度的高低决定了序列是否存在变异情况，即最值点极可能成为序列的变异点。计算步骤如下：

(1)对时间序列{u(i),i=1,2,…,N}进行空间重构，重构维数为m，由此可以构造出一组维数为m的新向量X(1),X(2),…,X(N-m+1)，其中X(i)={u(i),u(i+1),…,u(i+m-1)},i=1,2,…,N-m+1；

(2)计算任意向量X(i)与其余向量X(j)之间的相对欧式距离d[X(i),X(j)]；

(5)维数m增加 1，重复步骤(1)～(4)，得Cim+1(i)和φm+1(r);

(6)近似熵的估计值定义为：

ApEn(m,r)=φm(r)-φm+1(r)

(1)

式中：ApEn的取值与m和r有关，Pincus建议取m=2，r=(0.1～0.25)σ，其中σ为原始数据的标准差[19]。

3.2.2 样本熵法 样本熵(SpEn)法由Richman和Moorman于2000年在近似熵法基础上提出，该方法克服了近似熵在计算时的偏差，近年来广泛应用于机械故障诊断和医学信号处理等领域[20]。该方法计算步骤与近似熵法类似，是对近似熵法的改进，详细计算步骤可参考文献[21]。

4 结果与分析

4.1 叶尔羌河源流区1957-2016年径流序列变化特征

1957-2016年卡群水文站年径流量变化过程线见图2(a)。从图2(a)可以看出，卡群水文站多年平均年径流量为67.08×108m3，年径流量序列呈锯齿状波动增加趋势，Mann-Kendall法检验统计量Z值为1.062，年径流量序列增加趋势不显著。由1957-2016年卡群水文站年径流量累积距平变化过程线(见图2(b))可以看出，1957-20160年年径流序列呈现出先下降后上升的“V”型阶段性变化特征。其中，1957-1963、2002-2016年呈显著上升，表明该阶段年径流量丰水期多于枯水期；1964-1976、1990-2001年呈显著下降，表明该时段年径流量丰水期少于枯水期；1967-1989年径流序列呈频繁波动，表明该时段年径流量处丰枯交替阶段。

图2 1957-2016年卡群水文站年径流量变化过程线及年径流累积距平变化过程线

4.2 Mann-Kendall法突变点诊断

运用Mann-Kendall法对卡群水文站1957-2016年径流量年序列进行突变点检验，结果见图3。

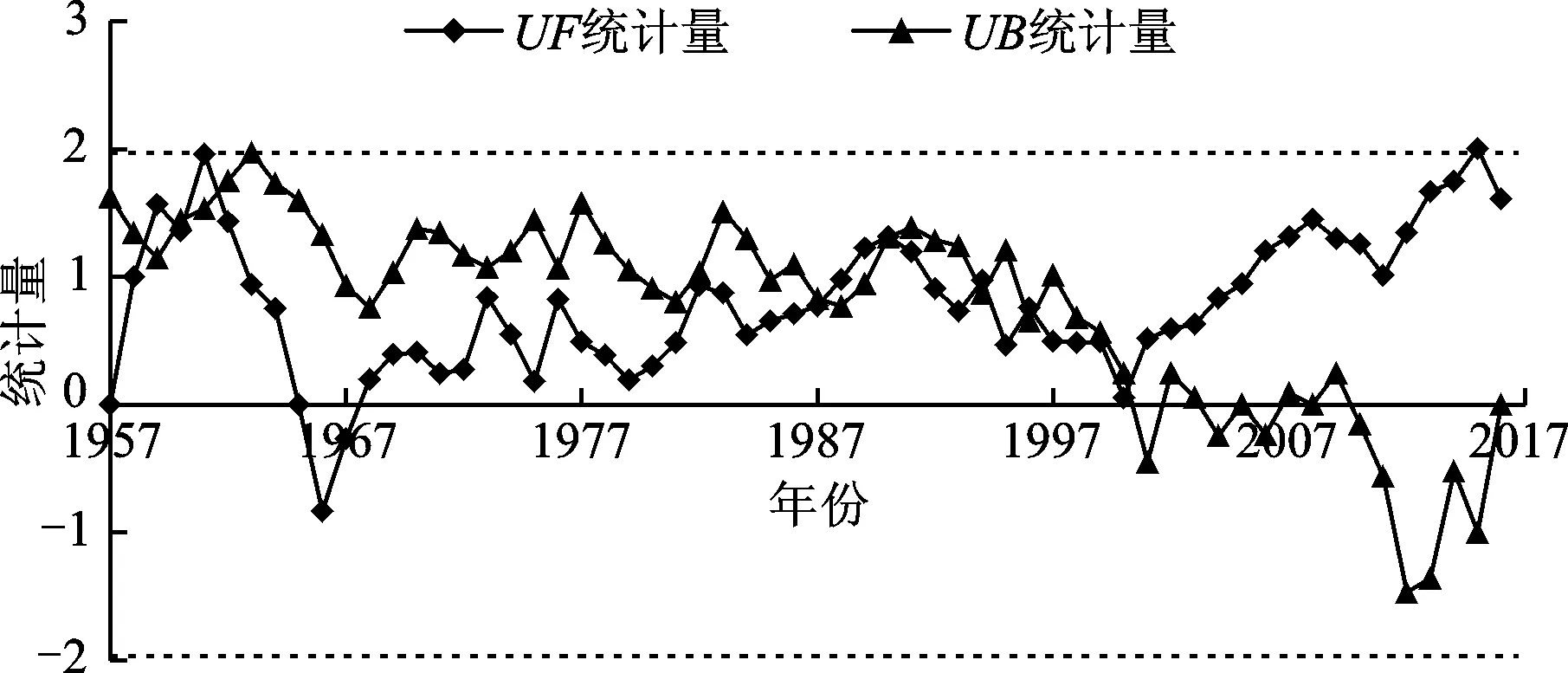
图3 叶尔羌河卡群水文站年径流Mann-Kendall突变检验过程线

由图3可以看出，在检验线之间(±1.96)UF和UB曲线共产生9个交点，分别为1958、1959、1960、1982、1987、1990、1994、1996、2000年，即该序列存在9个突变点。由于1958、1959、1960年这3个年份距离该系列的起始时间较近，靠近边界的交点尚需更长的水文资料进行验证，且短时间内不会出现频繁突变现象，故将该3个年份视为一个突变点，即1959年。此外，UF和UB曲线在20世纪80年代至90年代末产生多次交点，表明该时段内年径流呈波动趋势，丰枯突变较频繁，突变点较多，与实际情况不相符，且均未超过95%显著水平，突变不显著。通过以上分析表明，Mann-Kendall法诊断得出的突变点无法拥有足够论据判定变异点。

4.3 近似熵与样本熵法变异点识别与对比

4.3.1 近似熵法变异点诊断 1957-2016年卡群水文站日径流量序列近似熵值(ApEn)变化过程线见图4。依据近似熵计算步骤及文献[22]，本文取m=2，r=0.15σ，(σ为原始数据的标准差)。由图4可以看出，研究区日径流序列近似熵值变化过程可以分为4个变化阶段，分别为1957-1959、1960-1987、1988-2004、2005-2016年。其中，1957-1959年近似熵值呈持续增加；1960-1987年间近似熵值呈波动递增变化，1987年近似熵值达极大值，其径流复杂程度极高；1988-2004年近似熵值呈波动递减变化，2004年近似熵值达极小值，其径流复杂程度最低；2005-2016年近似熵值均高于2004年，可预测性降低。结合曲线趋势及复杂度可以判断，1959、1987、2004年卡群水文站径流序列发生了变异。

图4 1957-2016年叶尔羌河卡群水文站年径流量序列近似熵变化过程

4.3.2 样本熵法变异点识别 1957-2016年叶尔羌河卡群水文站日径流序列样本熵(SpEn)变化过程线见图5。依据样本熵计算步骤及文献[23]，本文取m=2，r=0.15σ(其中σ为原始数据的标准差)。由图5可以看出，研究区日径流序列样本熵值变化过程可分为3个阶段，分别为1957-1987、1988-2004、2005-2016年，整体上呈先上升后下降再上升的阶段性变化特征。1987年样本熵出现极大值，其径流复杂度最高；2004年样本熵出现极小值，其径流复杂度最低，可预测性最高。结合曲线趋势及复杂度可以判断，1987、2004年卡群水文站径流序列发生了变异。

4.3.3 近似熵法与样本熵法变异点识别效果对比 数据量越大，近似熵值越小[24]，当数据量小于一定程度时，近似熵不能反映序列真实的波动状态；同理，样本熵也存在相同情况。因此，两种方法在维数一定，相同数据量的情况下，统计值越大，表明波动越接近真实状态[25]。近似熵与样本熵法诊断结果对比曲线见图6，由图6可以看出，样本熵值大于同期近似熵值，且样本熵值变化幅度较近似熵值明显，表明样本熵具有灵活的敏感度，可更好反映径流量时间序列的波动情况，即更加适应径流量时间序列的变异点诊断。

图5 叶尔羌河卡群水文站径流量序列样本熵变化过程

图6 近似熵法与样本熵法诊断结果数据对比曲线图

5 讨 论

为了进一步验证样本熵法识别研究区径流序列变异点的可靠程度，对图5中径流量样本熵变化过程3个阶段内的均值、方差及变差系数进行比较分析，计算结果见表1。

表1 卡群水文站1957-2016年径流量序列分阶段均值、方差、变差系数参数

由表1可以看出：(1)1957-1987、1988-2004、2005-2016年3个阶段的年径流量均值呈先减少后增加趋势，1988-2004年均值最小，1988-2004年径流量均值相对于1957-1987年减少了14.88%，而2005-2016年径流均值相对于1988-2004年增加了20.39%；(2)1957-1987、1988-2004、2005-2016年3阶段的方差差异性较大，1988-2004年间的年径流量序列方差最小，说明该阶段离散程度越小，且1988-2004年径流量序列的方差值较1957-1987年减少了103.71%，2005-2016年径流量方差相对于1987-2004增加了122.89%；(3)1988-2004年间变差系数最小，相对于1957-1987减少了80%，2005-2016年径流变差系数较1988-2004增加了70%。从整体来看，无论是均值、方差，还是变差系数，均具有相似的变化规律，即呈先减少后增加的趋势，进一步验证样本熵识别的变异点可靠程度。

叶尔羌河属于融雪与雨水混合补给型河流，夏季融雪径流大，冬季径流量稳定[26]。径流量变异是不同驱动因素(人为因素、自然因素)共同作用的结果，由于卡群站以上为高山分布区，人为干扰较小，自然因素成为影响研究区径流量变化的主要因素[27]。已有相关文献显示[28-29]，1986-1987年叶尔羌河流域气候转型显著，2001-2005年暖湿化趋势进一步加强。气温升高，水循环加快，使得上游冰川物质平衡处于波动状态，造成冰川融雪径流量增加及冰川阻塞溃坝型突发洪水。本文通过对1960-2016年叶尔羌河卡群站径流量、年平均气温和年降水量相关性分析以及数据统计(图7、8和表2)，所得结论与高鑫等[29]结果一致，即气温和降水量呈增长趋势，气温升高对径流量的影响远大于降水量的影响。

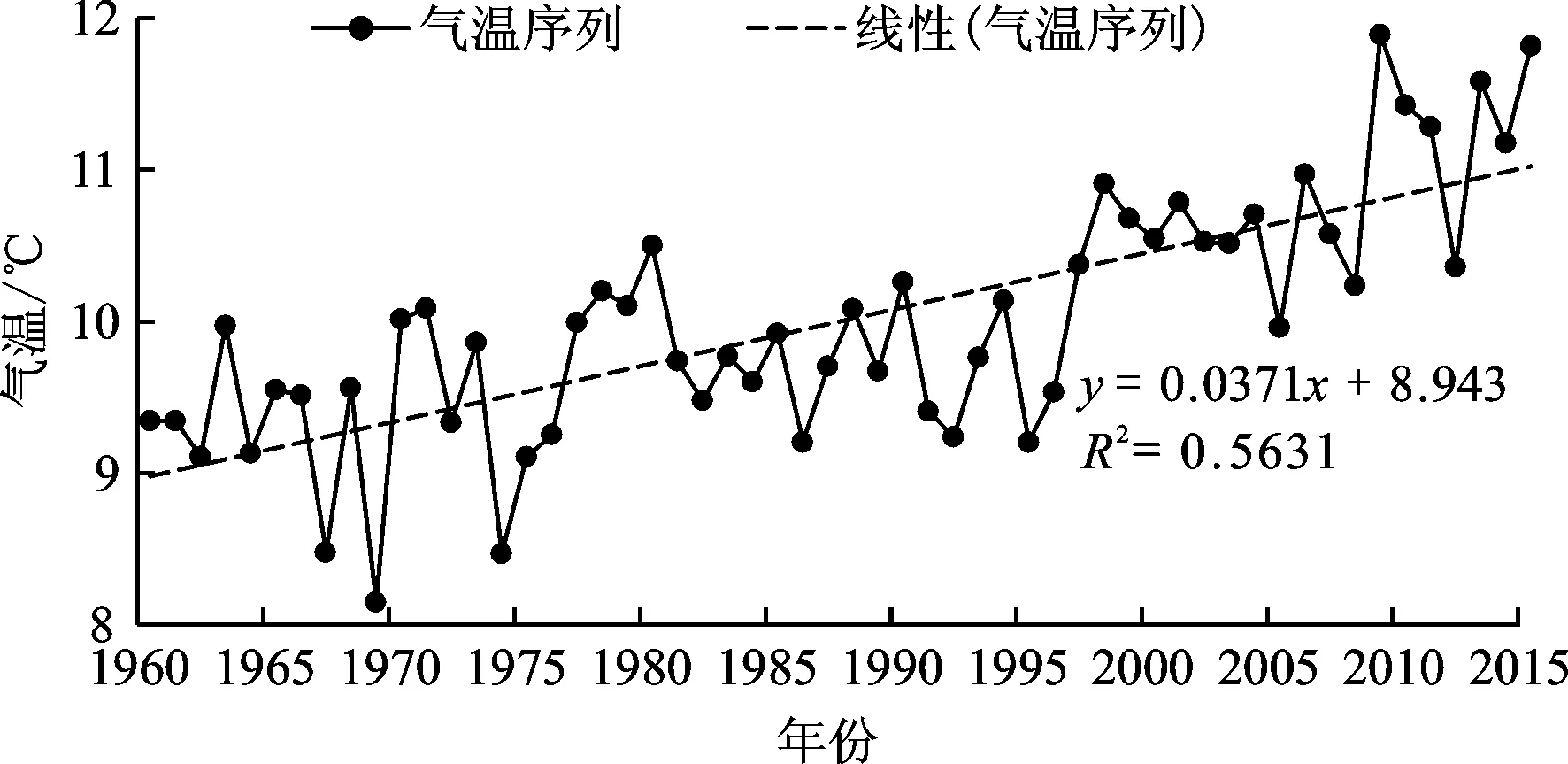
图7 1960-2016年叶尔羌河平均气温变化曲线

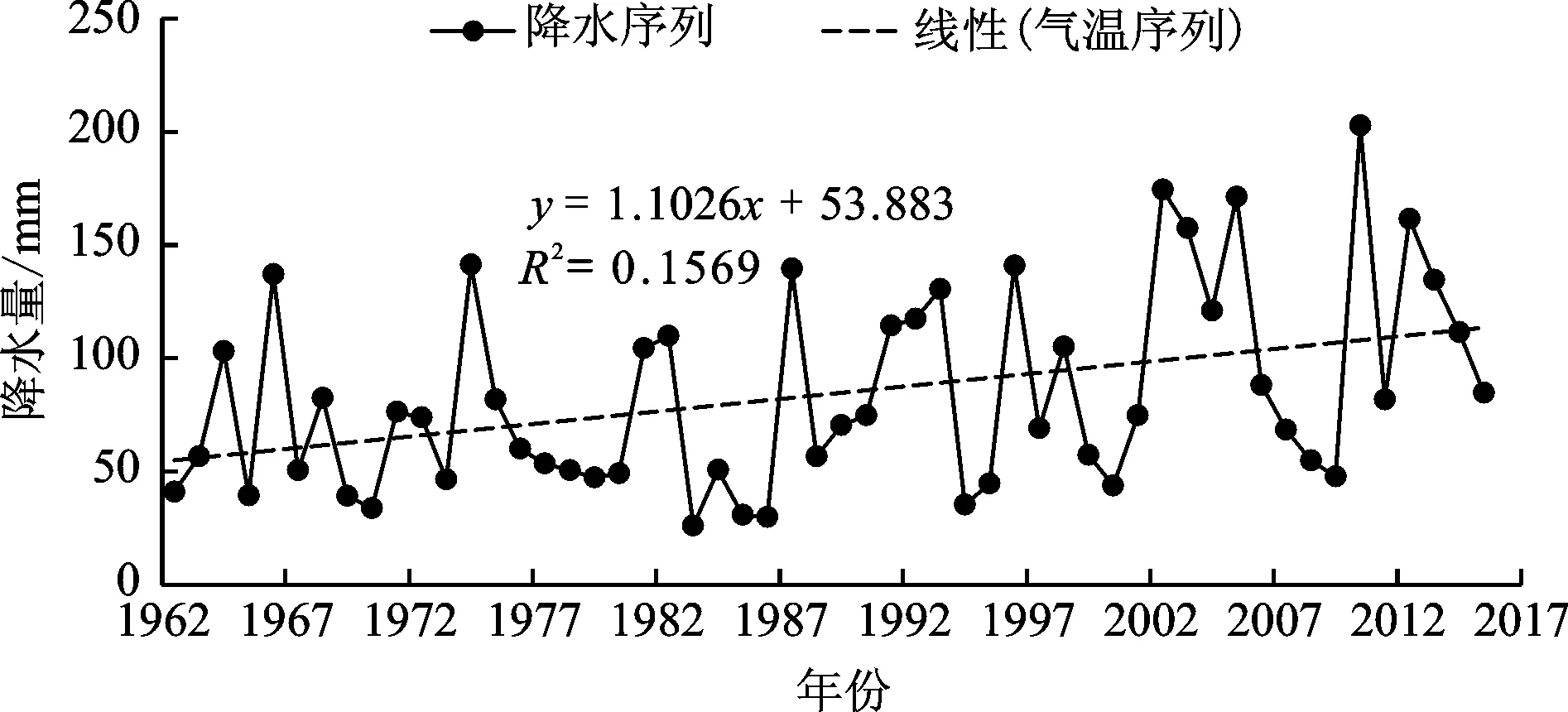
图8 1960-2016年降水量变化曲线

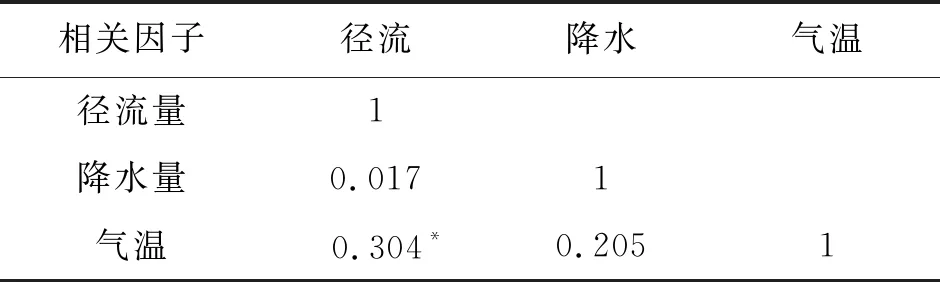
表2 1960-2016年卡群站径流量与降水量、气温因素相关系数

注：“*”表示通过0.05显著水平检验。

6 结 论

(1)采用传统的突变检验方法Mann-Kendall法对叶尔羌河出山口卡群水文站1957-2016年年径流量序列进行突变检验，发现出现多个虚假变异点，无法准确断定突变年份。

(2)采用近似熵法对径流量序列进行变异点诊断，发现1959、1987和2004年3个变异点，采用样本熵法对径流序列进行变异点诊断，发现1987和2004年两个变异点。通过两种方法的对比分析发现，在同一维度下，样本熵法较近似熵法能更好地反映径流量序列的波动情况，并且样本熵法具有更好的灵敏度。

(3)卡群站以上为高山分布区，人为干扰较小，自然因素成为影响研究区径流变化的主要因素。由于气候转型，气温升高，水循环加快，上游冰川物质平衡处于波动状态，造成冰川融雪径流增加及冰川阻塞溃坝型突发洪水。相关性分析结果表明，气温和降水量呈增长趋势，气温升高对径流量的影响远大于降水量增加的影响。