基于lp范数和融合字典的人脸识别算法
周 洋, 宋长明
(中原工学院 理学院, 河南 郑州 450007)
人脸识别是图像识别中研究最为广泛的一种技术,它通过比对人的脸部特征信息实现身份识别。但是,在光照、遮挡和采样不足等情况下,传统方法的人脸识别效果较差。因此,提高光照、遮挡和采样不足等情况下人脸识别算法的性能具有现实意义。
当前,稀疏表示方法在人脸图像识别领域得到了广泛研究[1-2]。WRIGHT等在2009年提出基于稀疏表示的分类(Sparse Representation-based Classification,SRC)框架[3],将稀疏表示成功引入图像识别领域。该算法以训练图像作为基准字典,采用稀疏表示对测试图像进行分类,能够较好地识别受噪声和遮挡等因素干扰的人脸图像。在WRIGHT等研究的基础上, DENG等在2012年提出了ESRC(Extended Sparse Representation-based Classification)算法[4]。该算法除基准字典外,以训练图像和测试图像之间可能的误差作为辅助字典,提高了采样不足情况下人脸识别算法的性能。2018年,DENG等受线性判别分析的启发,提出叠加线性表示分类(Superposed Linear Representation Classification,SLRC)的人脸识别算法[5]。该算法将测试样本表示为类中心矩阵和类内变化矩阵的叠加,有效地提高了对人脸单一样本图像的识别精度。以上算法在求解时均采用l1范数正则化方法,因此时间复杂度较高。而ZUO等研究认为,lp范数(0 目前很多主流的人脸识别算法都依赖于深度学习,例如DeepFace[9]、DeepID2+[10]、VGGFace[11]和FaceNet[12]等算法。虽然这些算法在实际应用中取得了很好的效果,但是深度神经网络往往需要大量的训练样本。此外,用于常规人脸识别的深度神经网络在遮挡等因素影响下并不具有很好的鲁棒性。 针对以上问题,本文从不牺牲算法运行时间的角度出发,在SLRC算法的基础上,基于lp范数正则化方法的优势,提出一种基于lp范数(0 在人脸图像识别应用中,稀疏表示方法是一种有效工具。通常情况是以给定训练图像来稀疏表示测试图像的。假设k类训练样本矩阵为A,且A=[A1,A2,…,Ak]∈Rn×m,其中,子矩阵Ai表示第i类样本,则任意测试样本y都可以通过训练样本矩阵A表示出来,即y=Ax。最初,在稀疏表示时,采用以下极小化目标函数,求得y=Ax的解。 (1) 式中:λ为正则化参数;‖·‖0为l0范数,用于计算x中非零元素的数量。 式(1)中l0范数极小化是NP难问题,研究者通常采用与l0范数最为接近的l1范数进行代替,即 (2) SRC算法采用式(2)作为目标函数,虽然在人脸识别方面取得了令人可信的结果,但是选取样本图像作为基准字典,在采样不足情况下的识别率仍会受到影响。在式(2)的基础上,SLRC算法首先将训练样本矩阵A∈Rn×m分解,得到类中心矩阵P∈Rn×k和类内变化矩阵V∈Rn×m,然后将测试样本表示为类中心矩阵和类内变化矩阵的叠加。该算法在描述样本差异的同时解决了单样本的字典完备性问题,改善了人脸识别算法在采样不足情况下的性能。 以上方法均采用l1范数求解稀疏性问题,虽然l1范数具有一定的有效性,但是并不能保证所获得的模型在多数情况下都具有最好的稀疏性。文献[13]认为,lp范数(0 (3) 目前,有许多求解lp范数稀疏编码的算法,如迭代重加权最小二乘(IRLS)[14]、迭代重加权l1极小化(IRL1)[15]、迭代阈值(ITM-lp)[16]、查找表(LUT)[17]和广义迭代阈值(GISA)[6]等算法。在某些情况下,前3种算法无法求得全局最优解,LUT算法需要计算存储查找表。相比之下,GISA算法更可靠,可以获得更精确的解。在文献[6]中,ZUO等采用GISA算法求解原始的SRC模型,展示SRC算法对于不同p值的识别率,取得了很好的效果。因此,在一定程度上,lp范数要优于l1范数。 本文基于lp范数(0 (1) 将训练样本图像矩阵A∈Rn×m分解为类中心矩阵 P=[c1,…,ci,…,ck]∈Rn×k (4) 和类内变化矩阵 (5) 式中:ci表示第i类的质心;ei=[1,1,…,1]T∈Rni×1。 (2) 融合类中心矩阵P和类内变化矩阵V,作为融合字典[P,V]∈Rn×(k+m),则融合字典可稀疏表示待测定的样本y,即y=[P,V][α,β]T。融合字典采用类中心矩阵描述光照、遮挡情况下样本的误差,采用类内变化矩阵来增强采样不足情况下字典的完备性。当一类训练样本不足时,融合字典中的类内变化矩阵V来自训练集外的其他图像。因此,基于lp范数(0 (6) (7) 即 (8) 这里借鉴文献[6]提出的一种泛化软阈值算法(Generalized Soft-Thresholding,GST),可以有效求解该问题。 给定p和λ,存在如下阈值: (9) (1) GST算法(算法1): (a) 输入:测试样本y,参数λ>0,p值,迭代次数J; 按照GST算法原理,式(8)可转化为如下形式: (10) (2) 求解式(6)的算法可总结如下(算法2): (a) 输入:测试样本y,参数λ>0,p值,迭代次数J; (c) 循环以下步骤: 在解决式(6)的求解问题后,与第i类相关的测试样本可近似表示为: (11) (12) 进而给出如下分类方法: label(y)=arg miniri(y) (13) 式中,label(y)为测试样本y的类标签。 综上所述,本文提出如下基于lp范数(0 (a) 输入:训练样本矩阵A=[A1,A2,…,Ak]∈Rn×m,测试样本y,参数λ>0; (b) 利用式(4)和式(5)计算融合字典[P,V]; (c) 利用主成分分析(PCA)法计算投影矩阵Φ∈Rd×p,并将融合字典[P,V]降维,[P,V]←ΦT[P,V]; (d) 将融合字典[P,V]归一化; (f) 利用式(12)计算残差ri(y); (g) 输出:测试样本y的类标签label(y)=arg miniri(y)。 为检验算法的性能,可选择SRC、ESRC、SLRC、SRC-p算法和本文算法进行仿真,并采用PCA法降低样本的特征维度。实验在Matlab R2011a软件环境下Intel Core i5-4200 M 2.50 GHz计算机上进行。 为了测试参数p取不同值时本文算法的性能,在Extended Yale B数据库上进行了实验。该数据库包含64种不同光照条件下38个人2 432张正面人脸图像,每张图像的分辨率为168×192。图1所示为Extended Yale B 数据库的部分图像。 图1 Extended Yale B数据库的部分图像 为了降低各种算法的计算成本和内存占用量,可将这些图像裁剪为32×32维。实验中针对每个人选择16张样本图像用于训练,剩余样本图像用于测试。本文选用100维的特征空间进行实验。p取不同值时的人脸识别率如图2所示。 图2 p取不同值时的人脸识别率 分析图2可知:SRC、ESRC和SLRC算法对应曲线为水平线,均是采用l1范数求解的,识别率不受p值影响;SRC-p和本文算法采用lp范数求解,因此识别效果会随参数p的变化而改变;从整体来看,本文算法的识别率在多数情况下要优于其余4种算法。具体来说,当p=0.5时,本文算法的识别率达到最高,为67.33%,分别较SRC、ESRC、SLRC以及SRC-p方法提高了5.15%、2.58%、1.43%、1.97%。因此,以下实验中将设置p=0.5。 为了检验采样不足条件下本文算法的性能,从Extended Yale B数据库中先后选择8张、12张、16张样本图像用于训练,剩余样本图像用于测试。图3所示为SRC、ESRC、SLRC、SRC-p和本文算法在采样不足条件下的识别率。 (a) 8张训练样本 (b) 12张训练样本 (c) 16张训练样本图3 采样不足条件下的识别率 从图3可以看出,对比其他4种算法,本文算法的识别率在不同特征维数下均有显著提高。由此可见,基于lp范数和融合字典的人脸识别算法是非常有效的。 为了进一步比较采样不足条件下各种算法的性能,本文选择4~16张不同数量的训练样本进行实验。图4为1 024维下5种算法对不同数量训练样本图像的识别率。 图4 5种算法对不同数量训练样本图像的识别率 从图4可以看出,在训练样本数量变化的情况下,本文算法较其他算法的识别率均有显著提高。由此可见,采样不足条件下本文算法具有更好的鲁棒性。 为了进一步对比不同算法的性能,本文将测试不同算法的总运行时间,并计算单张图像的运行时间。从Extended Yale B数据库中针对每个人,选择16张样本图像用于训练,剩余样本图像用于测试,并将图像裁剪为32×32维。表1所示为Extended Yale B数据库上不同算法的识别率和运行时间。 表1 Extended Yale B数据库上不同算法的识别率与运行时间 从表1可以看出,本文算法和SRC-p算法明显耗时较短,并且识别率均高于SRC、ESRC和SLRC算法。这是因为lp范数正则化方法容易求解,能够得到比l1范数更稀疏的解。与SRC-p算法相比,本文算法识别率提高了2.25个百分点,总运行时间缩短了5.58 s,单张图像运行速度提高了1.39倍(按8.21÷5.92计算)。这进一步表明,本文算法无论在识别率还是运行速度上均具有明显优势,更适合在大规模的人脸识别中应用。 同样,可在ORL数据库上进行实验。ORL数据库是由40个人、每人10张、像素92×112的正面人脸图像构成的。这些图像均受不同光照和面部表情的影响。图5所示为ORL数据库的部分图像。 图5 ORL数据库部分图像 实验时从ORL数据库中针对每个人选取5张样本图像进行训练,剩余样本图像用于测试。表2所示为ORL数据库上不同算法的识别率和运行时间。 表2 ORL数据库上不同算法的识别率和运行时间 从表2可以看出:SRC、ESRC和SLRC算法的识别率相同,这是因为本实验选用的是ORL数据库,虽然同类样本中间存在差异,但是差异并不明显;SRC-p算法的识别率较前3种算法提升了3.5个百分点;本文算法的识别率较前3种算法提升了4个百分点,仍为最优;从运行时间上看,SRC-p算法运行时间最短,本文算法次之,时间上毫秒级的延迟对于识别率的提升来说可以忽略。由此看出,本文算法同样适用于受光照、遮挡等因素影响较小的人脸识别。 为了测试本文算法在每人只有一个训练样本情况下的性能,实验方案按照经典文献中ESRC算法采用的AR人脸数据库实验[4]来确定。AR人脸数据库包括在表情、光照和遮挡等因素影响下的126人4 000多张正面脸部图像,每张图像的分辨率为165×120。图6所示为AR数据库部分图像。 图6 AR数据库部分图像 实验样本图像来自50名男性和50名女性构成的子数据库。首先选择80个人、每人13张样本图像,使用自然表情和光照的单张样本图像进行训练,而将其余12张受光照、表情和遮挡影响的样本图像用于检测;然后从剩余的20人中选择每人12张样本图像,组建类内变化矩阵。为方便测试,将图像裁剪为27×20维。表3所示为AR数据库上单一训练样本实验不同算法的识别率。 表3 单一训练样本的不同算法识别率 % 注:实验采用AR数据库。 SRC和ESRC算法的识别率与文献[4]中的数据相吻合。虽然SLRC算法将训练样本矩阵作为类中心矩阵,ESRC算法将训练样本矩阵作为类内变化矩阵,但由于二者均采用单一样本训练,因此SLRC和ESRC的识别率一样。本文算法的识别率,与SRC相比提高了34.9个百分点,与ESRC和SLRC相比提高了3.44个百分点,与SRC-p相比提高了34.48个百分点。因此,本文算法在单一训练样本的实验中具有更好的效果。 针对传统人脸识别算法在光照、遮挡和采样不足等情况下识别率低、运行速度慢的问题,本文提出一种基于lp范数(01 相关工作
1.1 稀疏表示模型
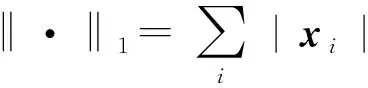
1.2 lp范数表示模型
2 基于lp范数和融合字典的人脸识别模型
2.1 模型提出
2.2 模型求解
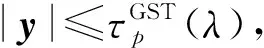


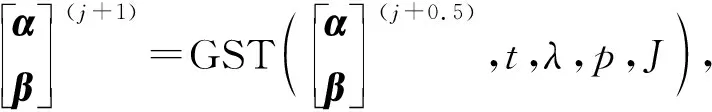
2.3 算法表示
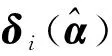

3 实验
3.1 p取不同值时的人脸识别


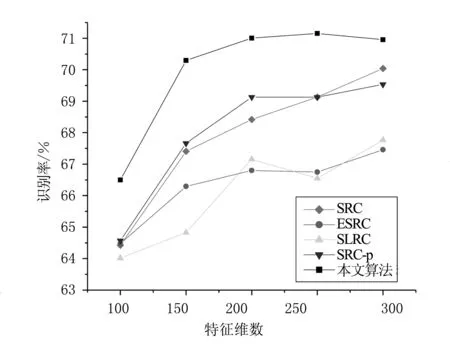
3.2 采样不足条件下的人脸识别



3.3 运行时间对比

3.4 ORL数据库上的人脸识别


3.5 单一训练样本的人脸识别


4 结语

