基于对抗自编码器的融合数据标签新奇检测研究

刘凤华， 李正伟， 刘小明, 杨 关

(中原工学院 计算机学院， 河南 郑州， 450007)

随着深度学习的发展，深度卷积网络在解决各种视觉识别问题上取得了显著进展。经典的图像识别网络有AlexNet(2012)、VGGNet(2014)、GoogleNet(2014)、ResNet(2016)、SENet(2017)等。在数据集IamgeNet分类识别任务中，机器已经超过了人类的识别水平。卷积神经网络模型在各种实现中逐渐成为图像处理的主流，这种具有多阶段图像特征的学习网络架构，通过监督大量的训练数据获得性能的提高。然而，在测试过程中，这种强监督学习的神经网络模型可能把不同于训练集中的类别实例当作异常数据给出不可靠的低预测置信度，或者当作正常类别给出较高的预测置信度。新奇检测能够解决这一问题。新奇检测是异常检测的泛化，它关注训练数据集中所没有的新奇类别。例如工业异常检测，流水线上的零件不可能都是合格的产品，需要设计图像处理算法识别出残次品。这就要求新奇检测模型不仅要对训练数据集中的正常类别对象进行准确识别，还要对训练数据集之外的异常类别对象进行有效处理。新奇检测是图像识别从闭集假设到开集假设的一个重要的研究方向。现实世界中的图像种类是无法穷尽的，训练数据集中不可能包括所有的图像类别。针对现实世界的图像识别任务，新奇检测模型投入使用时输入的图像数据不可能都是训练数据中的图像类别，这就需要图像识别模型能够允许在正常的数据中有其他类别的异常样本，测试时允许将未知的类别对象提交给算法。近几年研究人员探索了终身学习[1-2]、转移学习[3-4]、领域适应[5]、零样本[6-8]、单样本(少样本)学习识别[4，9]。这些研究领域均和新奇检测有着密切的关系。

1 研究现状

从统计学的角度来看，新奇检测通常发生在正常类别的数据分布是唯一可用的先验知识情况下。例如，在相关的工业故障检测现实场景中，工业故障的出现通常是毁灭性的和不可再现的，所以异常数据可能是非常罕见的，甚至是非常危险的，不可能依靠异常数据来评估工业机械的性能。因此，有必要依赖正常类别数据训练模型。

统计方法通常侧重通过学习概率模型的参数来建模正常类别的分布，将异常类别识别为概率较低的异常值。基于距离的新奇检测方法通过计算异常样本和正常样本的距离来识别离群点，假设正常类别相互接近，异常样本则远离正常类别的样本。BREUNIG等提出了LOF( Local Outlier Factor)算法,它是基于K近邻和密度估计的一种离群点检测方法，用来发现那些有意义的异常值[10]。PAUL等介绍了KNFST变换(Kernel Null Foley-Sammon Transform)的多类新奇检测,将每个已知类别的训练样本投影到核空间的一个点,通过计算测试样本和类代表的投影之间的距离来获得一个新奇测度[11]。LIU等改进了核零空间判别分析(KNDA)方法，提出了基于增量核零空间的判别分析(IKNDA)方法，显著降低了计算的复杂性[12]。

深度学习方法出现后，新奇检测的性能有了很大提高。由于异常数据点不具有稀疏表示，因此研究者们提出一系列自表示方法来检测异常对象。WANG等采用基于生成对抗网络(GAN[13])的方法，生成了与训练数据相似的新样本，证明了模型描述训练数据的能力，可将正常数据的隐式描述转换为一个新奇度评分[14]。XIA等通过减小自编码器的重构误差，从有噪声的数据中剔除异常数据，并利用自编码器的梯度大小使重构误差对正样本更具鉴别性[15]。然而，这些生成重建的方法在训练阶段都没有考虑数据集的标签信息。本文基于对抗自编码器的生成概率新奇检测[9]，通过学习一个自动编码器网络来刻画正常类别数据分布流形；在数据训练阶段融入图像的标签信息，采用生成概率进行新奇检测。因此，新奇检测成为对测试样本的概率评价：判断生成概率是否低于训练数据集中正常类别的概率阈值。

2 融合数据标签的新奇检测

2.1 对抗自编码网络模型

模型中的编码器g和解码器f组成自动编码网络。自动编码网络的训练应该尽可能地接近数据的真实流形。如果流形M表示描述某种图象类别的分布，编码器g和解码器f就能够通过训练学习重建生成此类图像。模型使用编码器g将图像实例x映射到潜在空间Ω中，用潜在空间向量z表示。为了使z的每个分量都具有最大的信息量，分量应为独立随机变量。判别器Dz使训练图像数据的潜在空间Ω接近一个正态分布N(0,1)，通过解码器f将潜在空间向量z重建成图像数据x||。经过大量数据的训练，模型的神经网络参数得到固定，程序可自动随机生成符合正态分布的向量z，将z输入解码器f，就可以生成正常类别的图像。这就意味着自动编码网络具有了利用符合正态分布的随机向量生成正常类别图像的属性。在潜在空间数据特征分布上进行采样，能够生成样例x∈M。将自动编码器重建生成的图像x||和原图像x输入判别器Dx，能进一步提升重建生成的图像质量。模型的总体架构如图1所示。

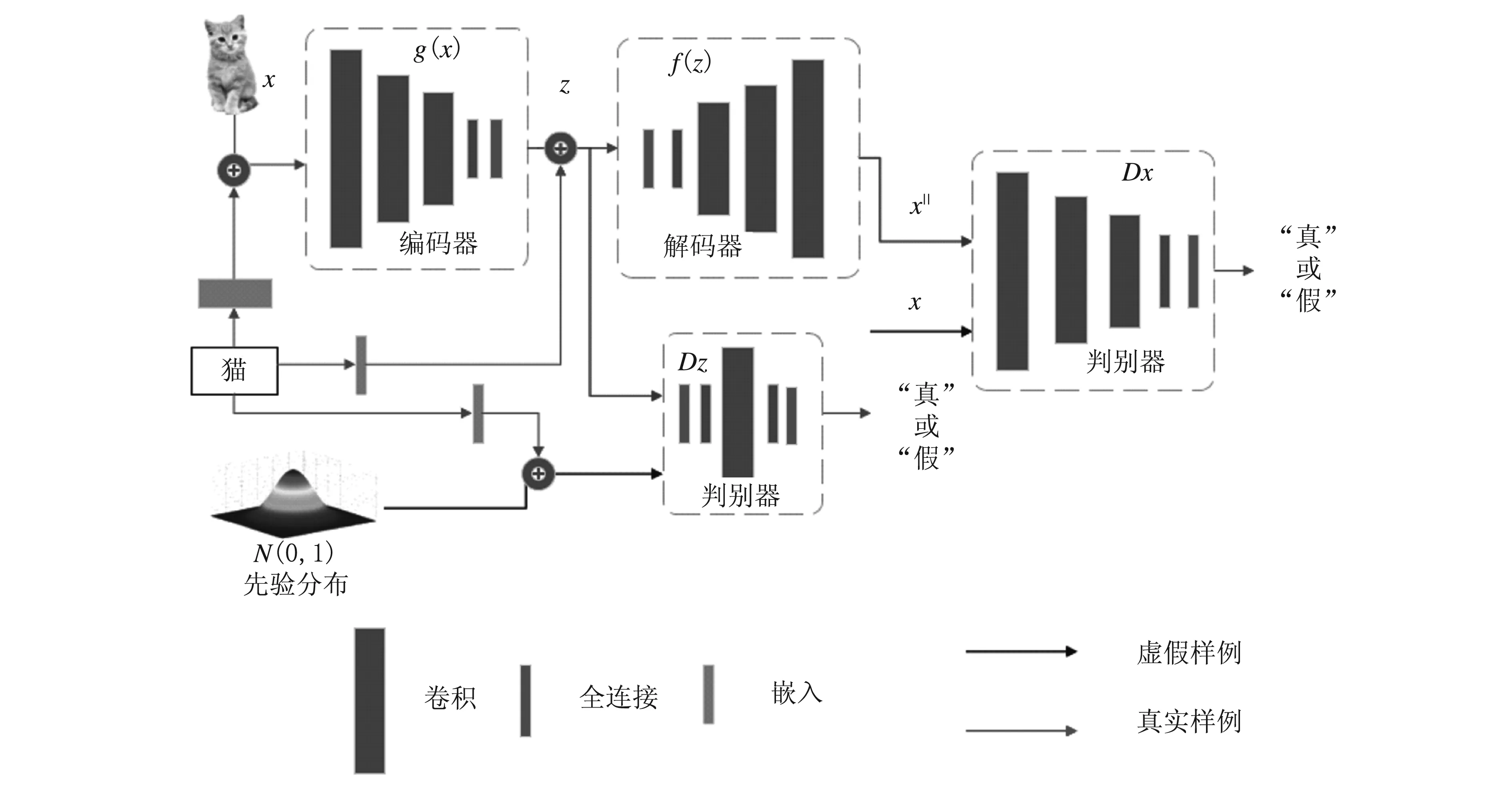
图1 模型整体架构示意图

训练数据集的标签能够增大测试数据集的正常类别和新奇类别特征之间的距离。本文将训练数据集的标签信息通过标签词嵌入的方式直接和图像、图像的潜在空间特征以及先验假设正态分布融合。在标签词嵌入过程中，对标签进行均匀分布的词嵌入，并且对词嵌入向量进行谱正则化处理[16]。

深度学习通过随机梯度下降的方式来降低模型的损失函数，通过迭代学习来提升模型的性能。本文模型的损失函数包括3项：①使用对抗性损失匹配图像数据潜在空间的分布与先验正态分布；②使用对抗性损失匹配潜在空间的解码图像的分布和已知的训练图像数据的分布；③使用自动编码器之间的损失评估解码图像和原图像之间的差距，即自动编码器的图像重建误差。

训练好的网络模型可以用来新奇检测。对于某一个测试样例图像数据x，通过下式进行新奇检测。

(1)

式中：γ是一个合适的阈值，Px(x)是图像数据的生成概率。

图2为新奇检测示意图。从图中可以看出，对潜在空间向量z进行了两个分支的处理：如果测试样例图像x的生成概率低于正常类别的阈值，就判定x属于新奇类别；否则，判定x属于正常类别。图2中x||是图像实例x经过自动编码网络生成重建得到的图像，识别器使用的是支持向量机(SVM)。

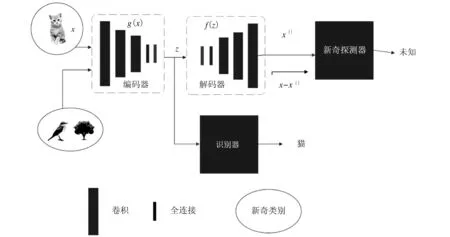
图2 新奇检测示意图

2.2 损失函数

损失函数用来估量神经网络模型的预测值与真实值的不一致程度，它是一个非负实值函数,通常使用来表示。损失函数越小，模型的鲁棒性就越好。本文模型包括两类损失：对抗损失和自动编码损失。

2.2.1 对抗损失

对于判别器Dz，使用以下对抗损失:

E[log(Dz(N(0,1)+EmbedN(y)))]+

E[log(1-Dz(g(x+Embedx(y))))]

(2)

式中：EmbedN(y)表示对标签y进行与正态分布N(0,1)相同维度均匀分布的词嵌入并进行谱正则化；Embedx(y)表示对标签y进行与图像数据x相同维度均匀分布的词嵌入并进行谱正则化。

编码器g尝试将图像数据x编码为潜在特征空间向量z，其分布接近正态分布N(0,1)。判别器Dz的作用是在神经网络模型的训练过程中区分编码器g产生的潜在空间向量z和先验正态分布N(0,1)，最终使z接近正态分布N(0,1)。编码器g试图最小化对抗损失，而判别器Dz试图最大化对抗损失。

同样地，对判别器Dx使用对抗损失:

E[log(1-Dx(f(N(0,1)+EmbedN(y))))]

(3)

解码器f试图从潜在空间中的潜在向量z生成重建图像数据x。判别器Dx的作用是在神经网络模型的训练过程中区分解码器f产生的生成样例和实际图像数据x，最终使生成图像更接近原图像。因此，编码器f试图使这个损失最小化，而判别器Dx试图使它最大化。

2.2.2 自动编码损失

模型联合优化了编码器g和解码器f，使属于已知数据分布的输入图像数据x的重建误差最小。

-Ez[log(P(f(g(x+EmbedX(y)))|x))]

(4)

通过最小化自动编码损失，促使编码器g和解码器f更好地逼近训练数据集正常类别的真实流形分布。

2.2.3 联合损失

以上所有损失的总和为:

(x,y,g,DZ,DX,f)=adv-dz(x,y,g,DZ)+
adv-dx(x,y,DX,f)+λerror(x,y,g,f)

(5)

式中，λ是一个平衡重建误差损失和其他损失的参数。

通过最小化式(5)，得到自动编码器网络的最优解为:

(6)

本文模型采用随机梯度下降法，对各损失分量进行交替更新训练，通过训练学习到网络模型的参数。

3 实验

MNIST数据集包含70 000张从0～9共10类手写数字图像，每一类手写数字图像有7 000张。神经网络模型训练时，随机从10类数字中抽取1类数字(例如数字7)的图像数据类别作为正常类别进行模型训练，其中图像数据的60%用于训练模型，20%用于验证模型性能，20%用于测试模型性能。模型在训练过程中的数据输入、重建和生成如图3所示。

图3 数据输入、重建与生成示例图

对于验证数据集和测试数据集，还可从其他9类手写数字图像中随机抽取一定比例的数据，作为未知的新奇类别进行图像增量测试模拟。在验证阶段,分别使用包含10%、20%、30%、40%、50%的新奇类别的数据集做新奇检测。通过对训练好的神经网络模型的验证，找到一个合适的概率阈值γ。

F1是综合考虑Precision(准确率)和Recall(召回率)的通用评价指标，可用来测量模型的效果，其定义公式分别为：

(7)

(8)

(9)

式中：Precision为预测结果是新奇类别的图像，实际也是新奇类别的概率；Recall为真实结果是新奇类别的图像被预测成新奇类别的概率；TP(True Positive)为真实值是新奇类别、预测值也是新奇类别的次数；FP(False Positive)为真实值是正常类别、预测值是新奇类别的次数；FN(False Negative)为真实值是新奇类别、预测值是正常类别的次数。

测试阶段同样使用包含10%、20%、30%、40%、50%新奇类别的数据集做新奇检测，并根据测试结果，分别对TP、FP、FN进行统计，用来计算模型新奇检测的F1值。

为了考察模型的鲁棒性，用不同类别的手写字体图像(例如数字8)对神经网络模型重复进行上述训练、验证、测试步骤。经过5次实验，计算出新奇检测模型的F1平均值。为评估本文模型的效果，选择了4种常见的新奇检测模型进行实验对比。计算出各模型的F1得分,并根据得分绘制出新奇类别不同占比下F1得分折线图，如图4所示。

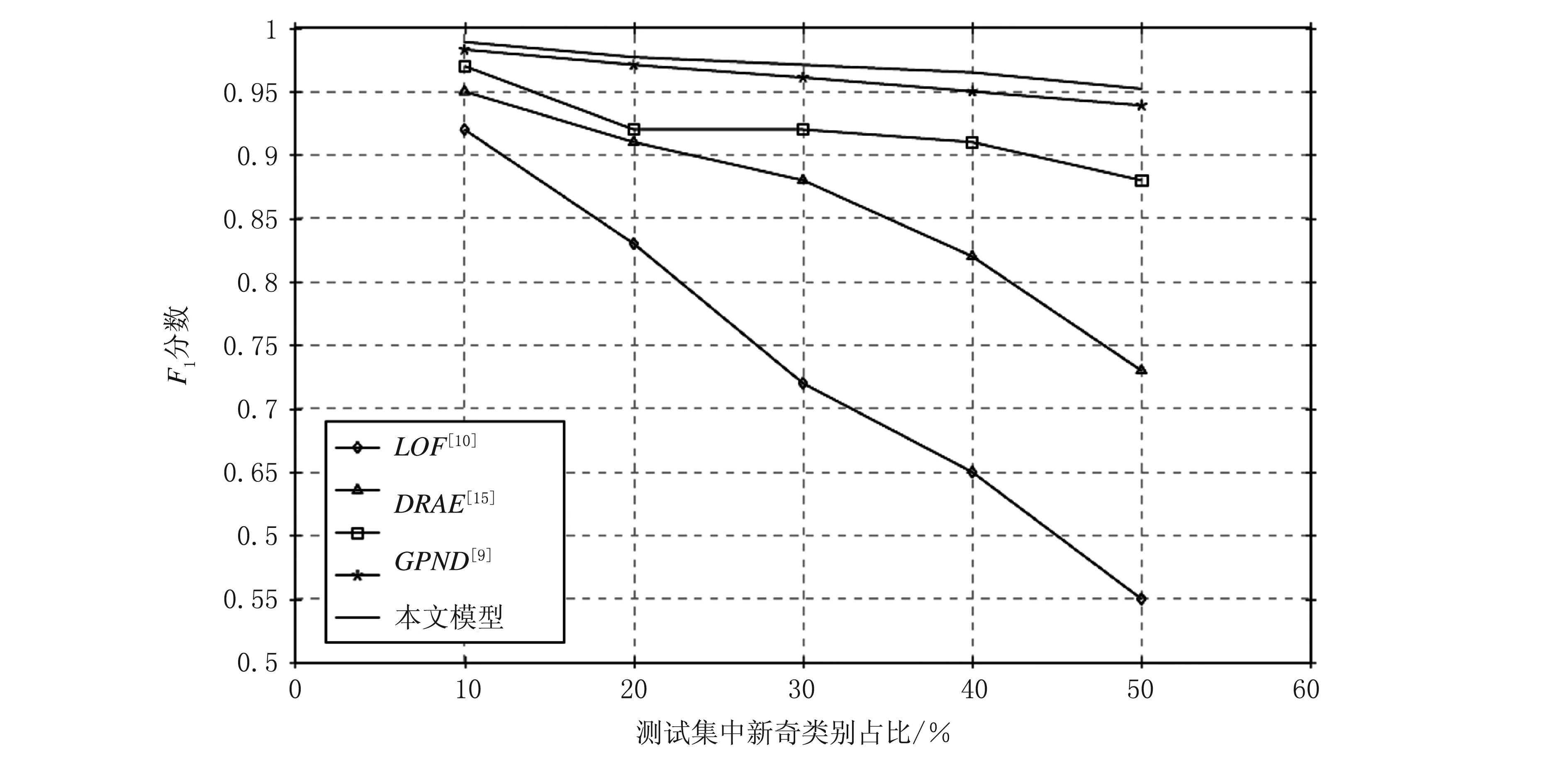
图4 新奇类别不同占比下各模型的F1得分折线图

本文模型在GPND模型[9]的基础上融入了训练数据集的类别标签信息。从图4可以看出，在不同新奇类别占比情况下，本文模型的F1得分都更高一些。由此可见，在模型训练阶段融入正常类别图像数据的标签信息是有效的。

4 结语

从闭集的图像分类到新奇检测，图像识别正在呈现新的发展变化。本文介绍了一种基于对抗自编码器的融合数据标签新奇检测模型，将训练数据集中正常类别图像数据的标签信息融入到训练过程中。通过与其他新奇检测模型进行比较，证明了融合数据标签的新奇检测方法是有效的。