基于ANSYS的混凝土随机骨料生成方法与细观破坏数值模拟
王彩峰, 贺 颖, 刘 振, 王一冰
(中建七局建筑装饰工程有限公司, 河南 郑州 450000)
混凝土是一种由粗骨料、砂浆和二者之间的胶结面所组成的三相非均质复合材料,其颗粒组成和级配对其宏观力学性能有重要影响。通过宏观力学性能试验去揭示混凝土内部结构的损伤演化过程,往往需要进行大量的实验,而实验结果的准确性还受到观测装置等因素的影响。随着计算机技术的快速发展,数值模拟方法越来越多地运用于材料破坏机理和宏观力学性能研究。数值模拟方法能够充分考虑骨料分布的随机性、材料的非均匀性以及各组分之间的相互作用,从细观层次上揭示混凝土内部的损伤和微裂缝的发展过程,而且数值模拟不受时间、场地、温度等条件的制约,能够避免实验过程中不利因素的影响。
对于混凝土的细观研究,最重要的是对混凝土内部结构进行仿真模拟。在混凝土中,骨料颗粒通常占总质量或总体积的70%以上,其形状、性能、配合比等决定了混凝土的性能[1],因此,混凝土骨料形状模拟是混凝土数值模拟的一个重要部分。国内外学者针对骨料的颗粒建模提出了很多数学模型,如WITTMANN等建立了角度和边数都随机的多棱角无规则的骨料模型,并采用BEDDOW等提出的方法自动生成圆形骨料[2-3];马怀发等对随机圆形骨料模型生成、网格剖分方法进行了研究,提出了随机骨料随机参数模型[4-5];王宗敏等提出了混凝土二维任意形状骨料随机投放方法,借助蒙特卡方法,采用极坐标的方式生成随机多边形骨料[6-7];高政国等提出以面积为参数的骨料侵入判别准则,按多边形随机生成方式建立了随机骨料的投放算法[8];侯宇星提出了一种以改进面积判别准则和凸多边形生成方式为基础的二维混凝土骨料随机生成算法[9],通过对骨料延伸条件的改进和定点位置条件的限定,提高了随机多边形骨料的生成效率;肖建强和夏晓丹在球形或椭球形的基础上采用渐变网格剖分的方法,在球体表面生成Delaunay三角形面单元,然后向里剖分,生成四面体骨料[10-11]。在上述骨料生成和投放算法的基础上,本文提出一种基于ANSYS的细密网格骨料构筑方法,该骨料生成算法建立在二维平面的基础上,在平面内生成多边形骨料颗粒,建立多边形平面方程,通过判别条件实现二维骨料颗粒的随机投放。
1 骨料生成算法
1.1 骨料尺寸和数目
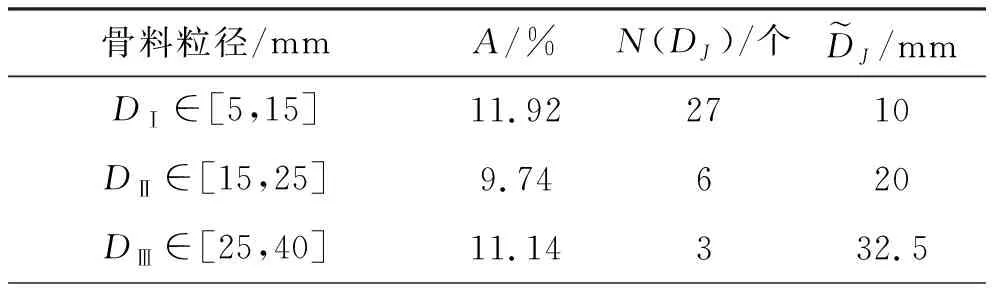
混凝土构件截面上随机颗粒尺度的概率分布满足Walraven公式[12],即:
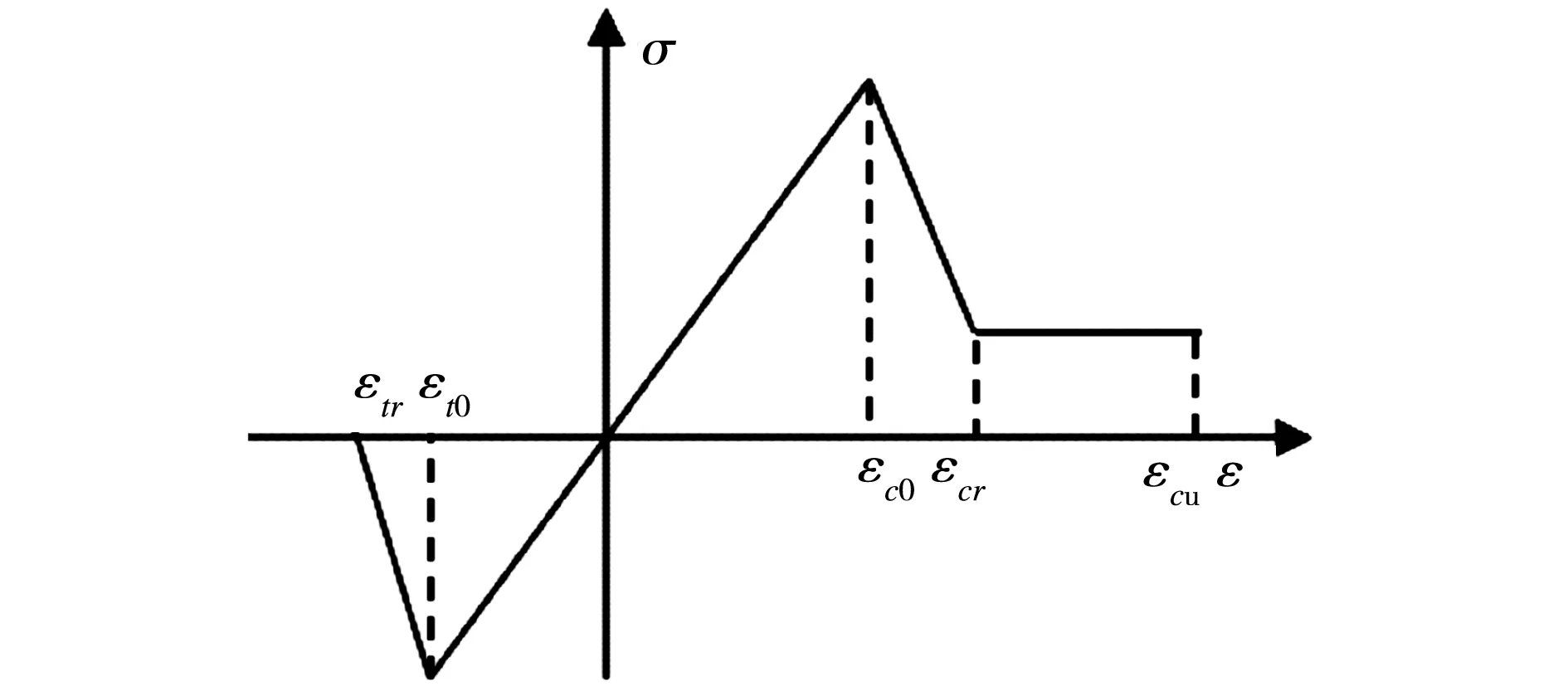
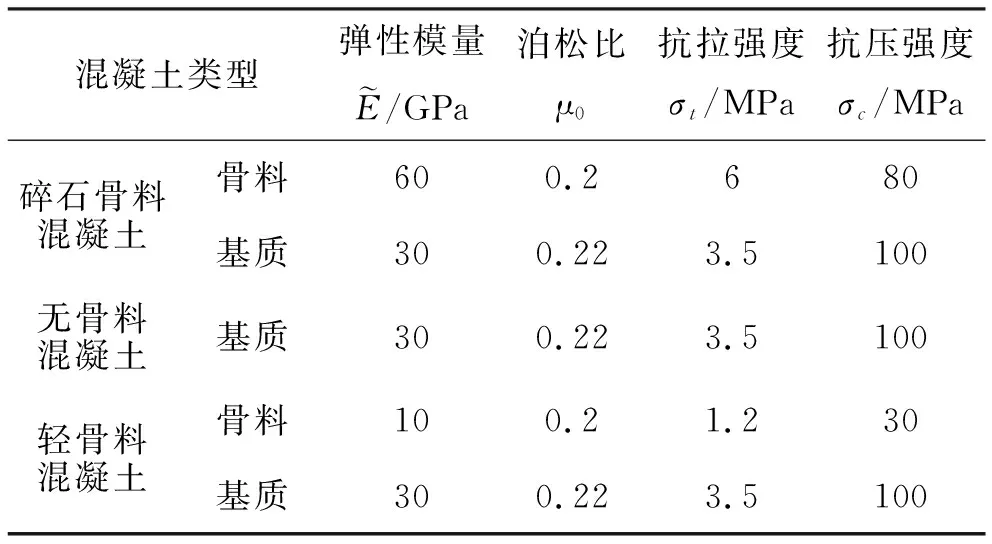
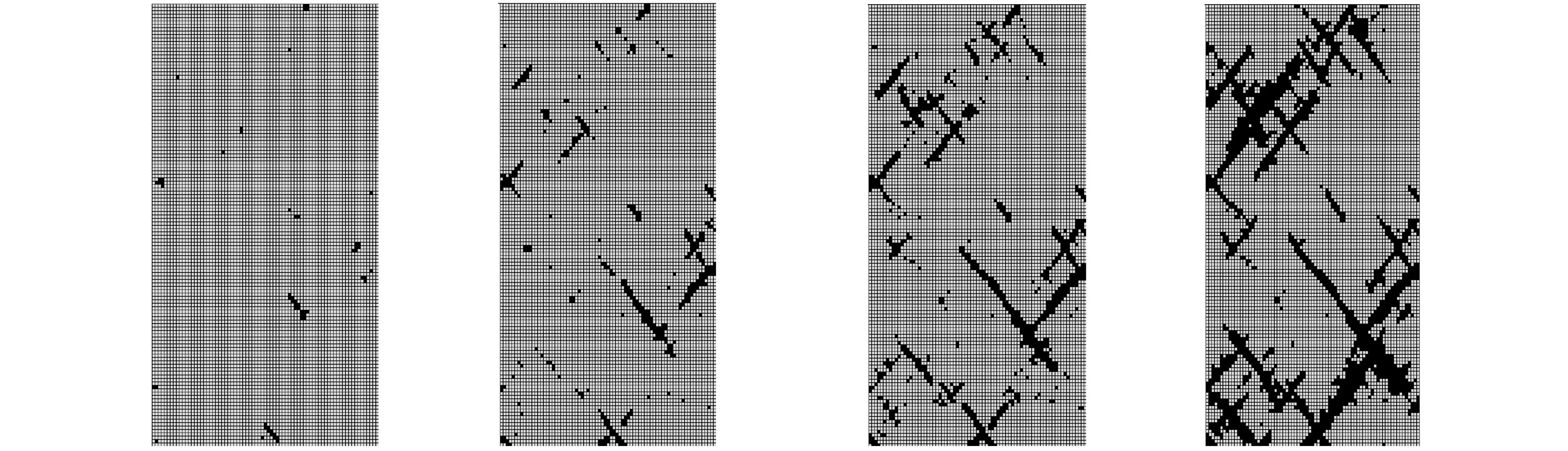
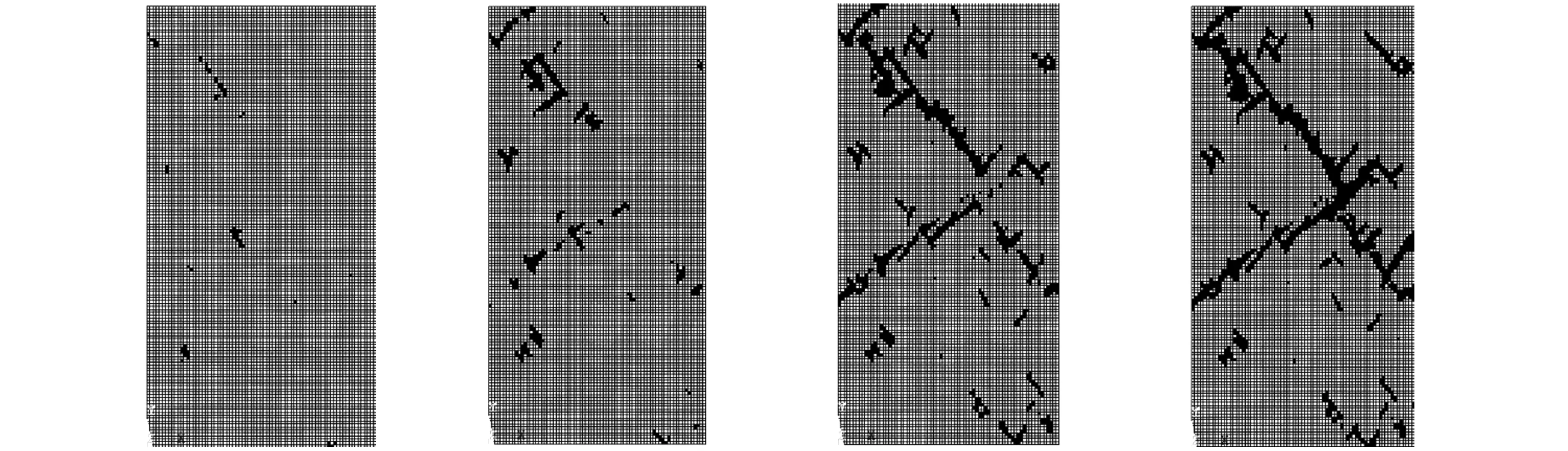
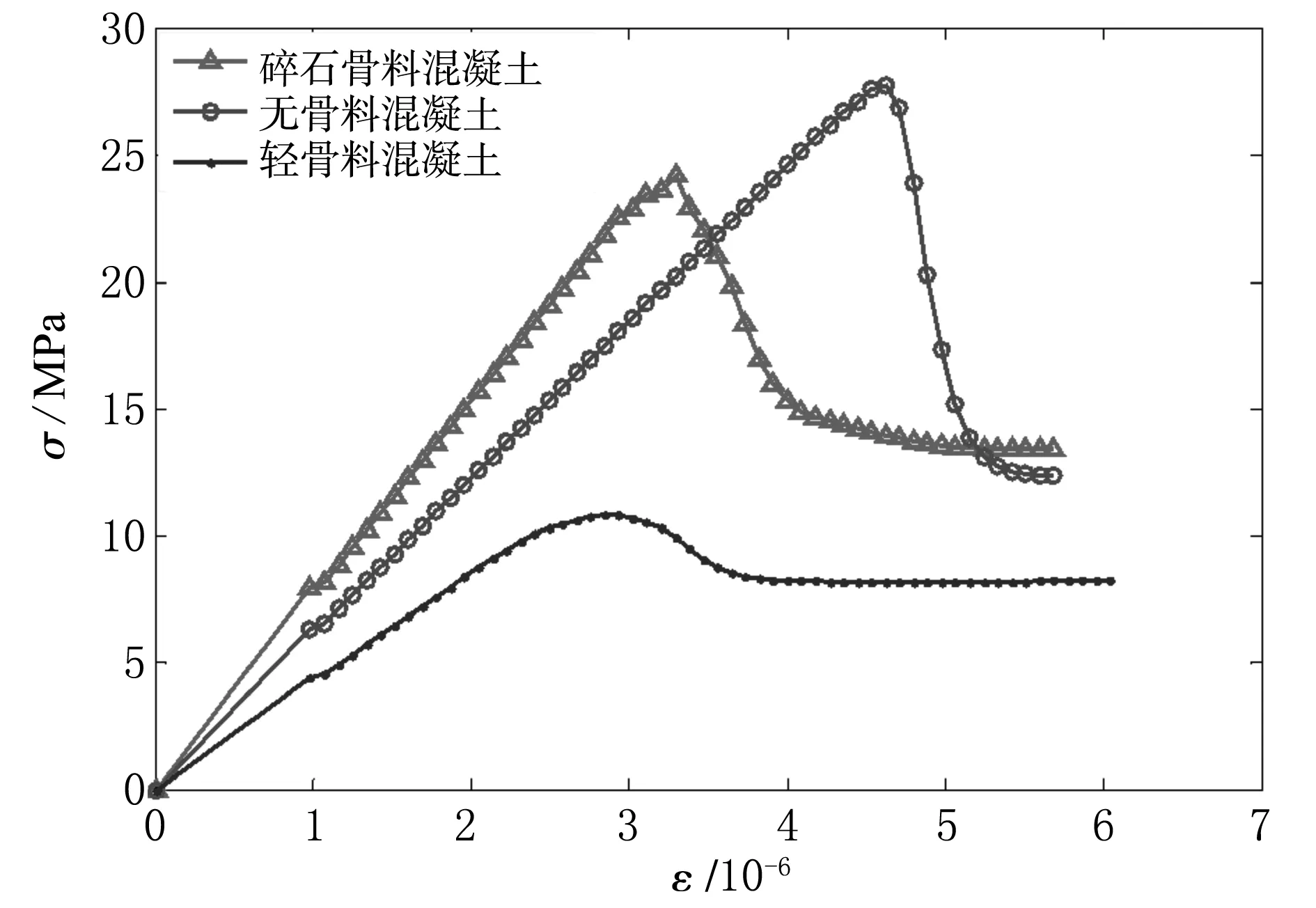
PC(D (1) 式中:PC为截面上任意粒径D 对于平面模型,已知骨料体积百分数为PK、总面积为A,Ⅰ、Ⅱ 、Ⅲ 3种骨料粒径的取值范围分别为D0∈[DⅠmin,Dmax],DⅡ∈[DⅡmin,DⅠmin]和DⅢ∈[DⅢmin,DⅡmin],则3种骨料颗粒所占据的截面面积为: A(DⅠ)=[1-PC(D A(DⅡ)=[PC(D A(DⅢ)=[PC(D (2) 这3种骨料颗粒数目为: (3) (1) 将Pi(i=1,2,3,…,n)点依次连线,形成n个直线方程Li(i=1,2,3,…,n); (2) 计算P0(x0,y0)到Li的代数距离d0i; (3) 对于截面上形心为P(x,y)的单元,计算P(x,y)到Li的代数距离di; (5) 遍历截面上所有的单元进行步骤(3)-步骤(4)的计算,即可在Pi点围成的多边形中识别出骨料单元。 (1) 从Ⅰ、Ⅱ 、Ⅲ3种骨料库中随机选取一种骨料,记为PT,初次随机试投放的位置记为PT(x,y)。 (2) 假设当前截面中已经就位的颗粒数为K,则形心Pi的位置记为Pi(xi,yi),其中i=1,2,3,…,K。 (3) 依次计算PT与形心Pi之间的距离‖di‖T以及它们之间的最小限定距离‖di‖=DT/2+Di/2,其中DT和Di分别代表颗粒PT与颗粒Pi的等效半径。 (4) 如果‖di‖T≥β‖di‖,则说明PT(x,y)满足第i个颗粒的就位条件,该条件数记为Ci=1,否则记为Ci=0。其中β是控制投放颗粒的稠密程度和穿插尺度的参数,该值越大,所投放的颗粒密度越小。 为了验证本文算法模拟混凝土骨料颗粒形状和投放的可行性,选取三级配混凝土模拟二维随机骨料颗粒生成。制作150 mm×150 mm的矩形截面,面积为A=22 500 mm2,选取的三级配混凝土配合比为小石∶中石∶大石=5∶4∶3,骨料体积比PK=0.448 3,各级配骨料粒径分别为:DⅠ∈[5,15]、DⅡ∈[15,25]和DⅢ∈[25,40]。通过式(1)和式(2)进行骨料颗粒的二维平面转化,计算出所投放各级配骨料截面所占模型截面面积的百分比和需要投放的颗粒数N(DJ),如表1所示。 表1 混凝土三级配骨料建模参数 注:A/%为各级配骨料截面所占模型截面面积的百分比。 按照表1给出的颗粒几何参数,首先在ANSYS中进行几何建模和网格划分,单元尺寸以基质中最小颗粒尺寸为最佳,然后利用APDL语言对上述颗粒生成算法进行编程,最后的生成结果如图1所示。其中,图1(a)为初次生成的矩形截面,图1(b)和图1(c)为经过切割加工形成的T形截面和回形截面。 为了验证该算法的颗粒投放效率,选取的模型尺寸为150 mm × 300 mm,采用的配合比同样为小石∶中石∶大石=5∶4∶3,模拟过程中投放骨料的截面所占模型截面面积的百分比不同,分别是35%、40%、45%、50%。生成结果如图2所示。 (a) 矩形截面模型 (b) T形截面模型 (c) 回形截面模型图1 三级配不同试件形状 (a) 35% (b) 40% (c) 45% (d) 50% (e) 实物图2 不同骨料面积投放率 投放结果表明,随着面积百分比的增加,投放模型颗粒饱和度逐渐增加。通过实物对比可以发现,在不考虑颗粒形状的条件下,50%面积百分比的投放模型基本接近实物饱和度。为了更加逼近实物模型,需要丰富颗粒形状、增加颗粒级配和面积百分比。 数值模拟的几何模型采用图2所示的一组骨料投放模型,对其中颗粒和基质赋予不同的材料参数,而同一种材料参数也是满足Weibull概率模型的随机数。这里只假设材料弹性模量E为随机值,其Weibull概率密度函数为: (4) 细密单元代表材料的基本组成单元,其破坏可用图3所示的损伤演化图描述[13]。 图3 损伤演化应力-应变关系图 受拉状态的损伤变量演化方程为: (5) 受压状态的损伤变量演化方程为: (6) 各向同性无损伤材料的应力-应变关系的二阶张量表达式为: σij=2Gεij+λδijεkk (7) 式中,G和λ为拉梅常数,即: (8) 各向异性损伤引起的各向异性的弹性矩阵为: E=E0(1-Dij) (9) 将式(9)代入式(7),可得各向同性的损伤应力-应变关系,如式(10)所示。 σij=(2Gεij+λδijεkk)(1-Dij) (10) 表2 3种类型混凝土材料力学参数 3种材料模型的破坏过程如图4-图6所示。可以看出,3种混凝土模型的破坏过程都具有阶段性,都可归纳为3个阶段:①微裂纹演化阶段,包含成核、生长和连接3个过程;②宏观裂纹成核阶段,表现为长大的微裂隙相互连接,形成裂隙网络,裂隙开始趋向集中,在断裂剪切带连接形成宏观裂纹;③宏观裂纹扩展阶段,表现为成核的宏观裂纹沿剪切带扩展、滑动,导致混凝土内部形成一条主裂缝带,贯通整个承载面,试件完全失去承载力。从断裂过程的损伤斑图可以看出,混凝土裂缝在初始阶段都是出现在混凝土内部薄弱位置,且破坏带沿近似45°剪切面扩展。上述破坏特征与试验室混凝土试件的破坏形态具有一致性,说明该算法能够从细观角度揭示混凝土宏观破坏过程。 (a) (b) (c) (d)图4 碎石骨料混凝土损伤演化图 (a) (b) (c) (d)图5 无骨料混凝土损伤演化图 (a) (b) (c) (d)图6 轻骨料混凝土损伤演化图 在细观破坏特征方面,3种材料差别明显:碎石颗粒混凝土(图4)裂缝绕开颗粒而沿基质扩展;轻骨料混凝土(图6)裂缝是在骨料内部成核、扩展,并且剪切带也主要沿骨料集中连接;无骨料混凝土(图5)裂缝表现为正常的共轭剪切断裂模式,剪切带与压应力方向基本为45°夹角。裂纹密度方面,无骨料混凝土密度较大,另外两种混凝土裂纹密度都较小。 从应力-应变曲线图(图7)可以看出,3种材料的承载性能都表现出弹性承载力增加和峰值后承载力下降的共性特征。但是承载性能的差异也是相当明显的,相比而言,无骨料混凝土最大强度值为28 MPa,碎石混凝土次之,其最大强度值为24 MPa,轻骨料混凝土强度最弱,其最大强度值为11 MPa,它们的最大强度值的比为2.6∶2.2∶1。可见,均质性决定材料的强度,均质性越高,材料强度越高;同时骨料强度决定混凝土的强度,骨料强度越高,混凝土强度越高。 从破坏特性来看,无骨料混凝土应力跌落速度快、跌落幅值大,说明其脆性较强,一旦破坏,可能导致材料迅速失稳;碎石颗粒混凝土应力跌落速度和幅值较前者小,说明其脆性有所降低,稳定性能略有改善;轻骨料混凝土在应力峰值后没有明显应力跌落,说明这种材料具有较好的延性破坏性能和良好的承载稳定性。 图7 混凝土应力-应变曲线图 本文提出了一种基于ANSYS的细密网格构筑任意形状骨料的方法,利用该方法可以随机生成任意形状的骨料,实现骨料颗粒的快速投放。这种算法采用单元编号来控制颗粒投放过程,不仅生成骨料速度快,而且在骨料投放上更具有先网格划分后随机投放的优越性,尤其可以避免骨料重叠性判断运算中的重复性计算。利用这种算法对三级配混凝土骨料颗粒生成进行模拟,验证了该算法模拟颗粒形状和投放效率的可行性,且生成颗粒的效果与真实混凝土接近。通过对碎石混凝土、无骨料混凝土和轻骨料混凝土进行单轴压缩破坏过程的模拟分析,揭示了它们破坏的共性特征和个性差异,为深入开展此类材料的研究提供了一种参考。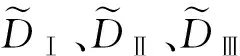
1.2 骨料形状控制


1.3 骨料随机投放
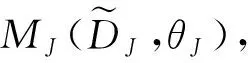
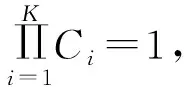
2 实例


3 混凝土破坏细观数值模拟
3.1 非均质材料模型
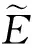
3.2 细观损伤准则与不可逆演化
3.3 单轴受压破坏数值模拟
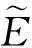

4 结论

