一类次临界增长非局部问题的无穷多解
2019-02-11 10:55吴燕林钱晓涛
延边大学学报(自然科学版) 2019年4期
吴燕林, 钱晓涛
( 阳光学院 基础教研部, 福建 福州 350015 )
本文考虑如下非局部边界值问题:
(1)
其中a,b>0, Ω是RN中的一个有光滑边界的有界区域,N≥3.
1 预备知识

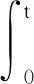
(f4)f(-t)=-f(t),∀t∈R.
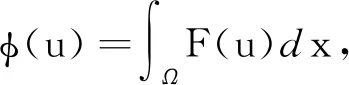



(2)
由式(2)可得
(3)
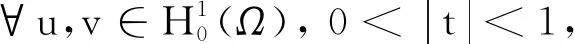
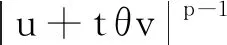

在空间L2(Ω)+Lp(Ω)中,定义范数


本文使用如下形式的对称山路定理(引理2)[8]证明本文的主要结果.

(I1)存在常数ρ,α>0, 使得I|Bρ(0)∩W≥α>0;

(I3)I满足(PS)c条件,其中0 显然问题(1)所对应的泛函为: (4) 定理1若条件(f1)-(f4)成立,则∀k∈N, 问题(1)存在k对非平凡解. 证明由引理1和条件(f4)可知,显然I是偶泛函,且I(0)=0.再根据引理2可知,只需验证泛函I满足条件(f1)-(f3)即可.以下分3步来证明. 所以 (5) 所以 综合以上3步知,对泛函I可以使用引理2,由此得问题(1)至少存在k对非平凡解.再由k的任意性可知,问题(1)有无穷多个解. 注1文献[1]的非线性项显然满足本文的条件(f1)-(f4),但本文得到的是无穷多个解,因此本文的结果拓展了文献[1]的研究结果.2 主要结果及其证明



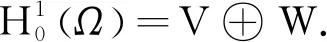


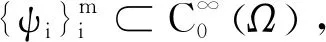
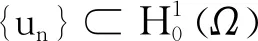



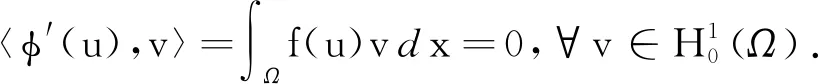
猜你喜欢
中等数学(2022年6期)2022-08-29
南方医科大学学报(2021年10期)2021-11-10
新世纪智能(数学备考)(2021年11期)2021-03-08
安阳工学院学报(2020年4期)2020-09-11
校园英语·上旬(2019年6期)2019-10-09
中学生数理化·七年级数学人教版(2017年6期)2017-11-09
中国校外教育(下旬)(2017年8期)2017-10-30
自动化学报(2016年3期)2016-08-23
少儿科学周刊·少年版(2015年1期)2015-07-07
小说月刊(2014年1期)2014-04-23

