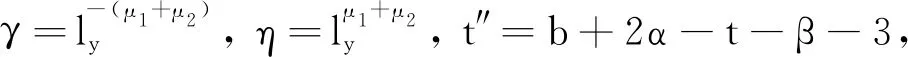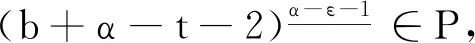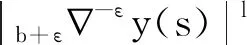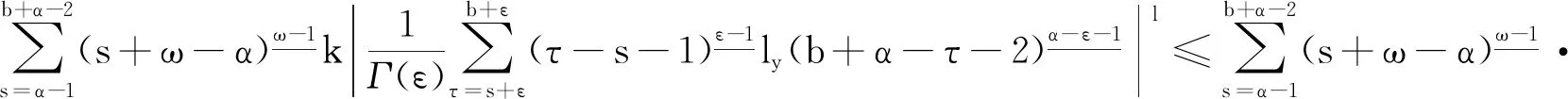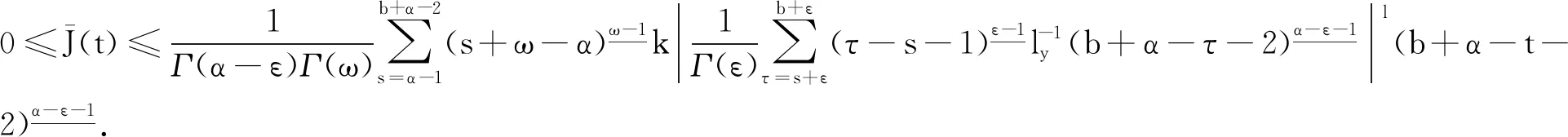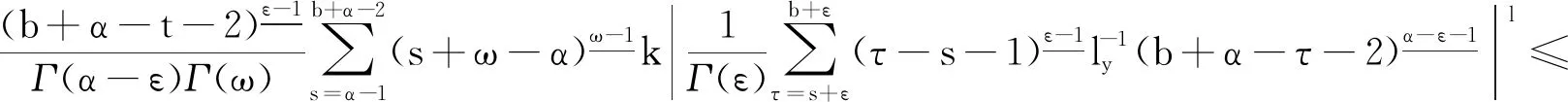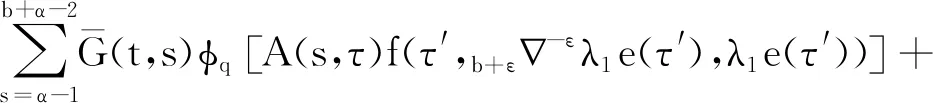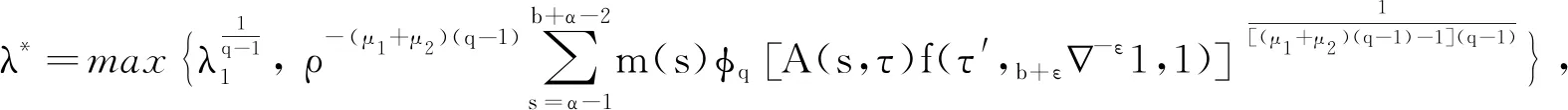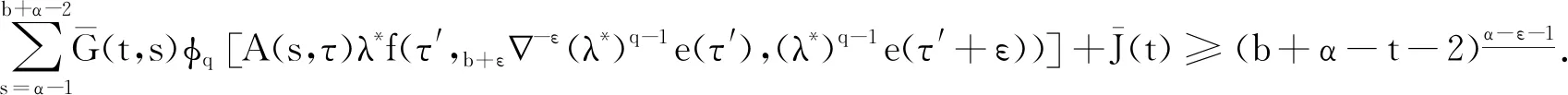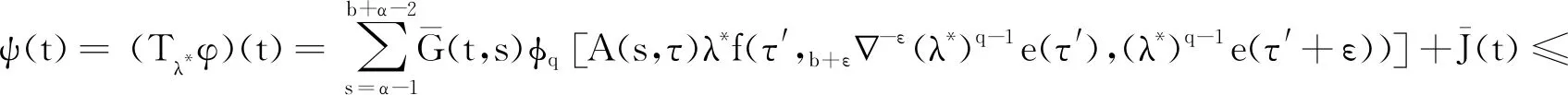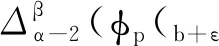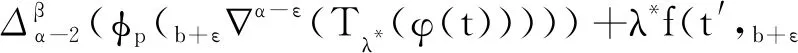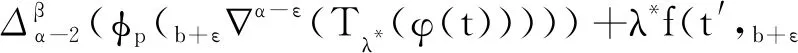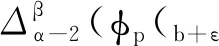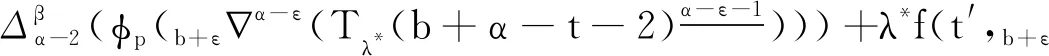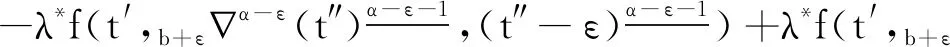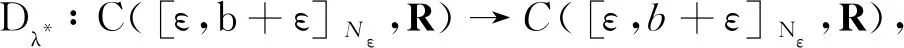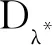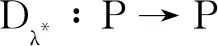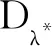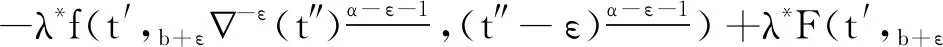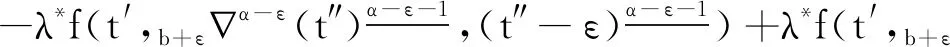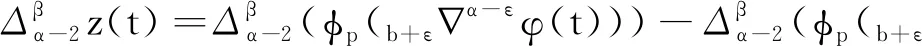具有p -Laplacian算子的delta-nabla分数阶差分边值问题正解的存在性
董强, 侯成敏
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
近年来分数阶差分系统受到很多学者的关注,其相关研究成果已逐步被应用在电气工程、化学和生物医学等领域中[1-4].在分数阶差分方程的相关研究中,其初值、边值问题解的存在性、唯一性和多重性等成为广大学者的研究热点[5-7].2017年Liu等[8]研究了如下带p-Laplacian算子的delta-nabla分数阶差分边值问题:
本文受文献[8]的启发,考虑在非齐次边界值条件下带有p-Laplacian算子的离散分数阶delta-nabla边值问题:
(1)
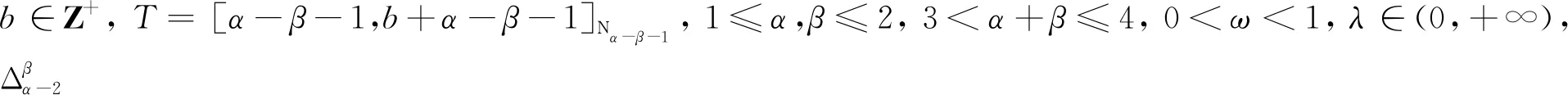
(H1)α,β∈(1,2], 3<α+β≤4,ω∈(0,1),α-ε-1>0.
(H2)g(t,x)是定义在[0,b]N0×(0,+∞)上的非负函数,且0≤g(t,x)≤k(|x|)l,l,k∈(0,+∞).
(H3)f∶[0,b]N0×R×R→[0,∞)是连续函数,对任何t∈[0,b]N0,f(t,0,0)≠0,f(t,1,1)≠0, 并令
(2)
1 预备知识
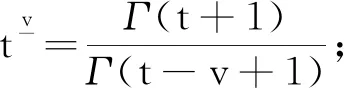
定义1[8]3设f∶Νa→R, 且v>0时,函数f的左分数阶和的定义为:
定义2[9]2设f∶bΝ→R, 且v>0时,函数f的右分数阶和的定义为:
引理1[9]3设b∈R, 当μ>0时,对于变量t有此外,对v>0,N-1 引理2[8]4设f∶Νa→R, 当v,μ>0且N-1 引理3[8]4设f∶bΝ→R, 当v,μ>0且N-1 b -μvb-μf(t)=bv -μf(t),t∈b -μ -N +vΝ. 引理5[9]3设f∶bΝ→R, 当v>0, 且N-1 (i)bvf(t)=(-1)NNb- (N -v)f(t). 引理6[8]4设f∶Νa→R, 当v>0,k∈Ν0时,对任意的t∈Νa +M -μ +v有 此外,若μ>0, 且M-1<μ≤M, 则对任意的t∈Νa +v有 引理7[8]4设f∶bΝ→R, 当v>0,k∈Ν0时,对任意的t∈b -vΝ有 此外,若μ>0, 且M-1<μ≤M, 则对任意的t∈b -M +μ -vΝ有 定理1设h∶[0,b]Ν0→R, 则nabla边值问题 (3) 所以 定理2设L∶[0,b]Ν0→R, 则边值问题 (4) 有唯一解u(s)=-φq[A(s,τ)λL(τ-α+1)].其中 证明由引理6容易验证定理2成立,故省略. 下面记τ′=τ-α+β+1,t′=t-α+β+1, 则由定理1和定理2可得方程(1)的解为 定理3设h∶[0,b]Ν0→R, 当1<α-ε<2时,nabla边值问题(3)等价于问题 (5) 证明假定x(t)是问题(3)的一个解,令y(t)=bεx(t), 则通过引理7及x(b)=0, 有y(b+ε)=0且x(t)=b + ε -1-εy(t).又因为bαx(t)=b -1αx(t)=b -1αb + ε -1-εy(t)=b + ε -1α - εy(t)=b + εα - εy(t), 所以问题(3)与问题(5)等价. 定理4当1<α-ε<2时,边值问题(1)等价于问题 (6) 证明证明类似于定理3的证明,故省略. 由此可知函数ħ(t,s)是关于t递减的,故 定理6称z(t)为问题(6)的下解,若函数z(t)满足不等式组 (7) 定理7称κ(t)为问题(6)的上解,若函数κ(t)满足不等式组 (8) 引理8(Schauder不动点定理) 设E是一个Banach空间,T∶E→E是完全连续映射,集合{x∈E:x=σTx}对0≤σ≤1是有界的,则T有一个不动点. 为了证明边值问题解的存在性,给出以下条件: (H4)f(·,u,s)∶[0,b]N0×[0,+∞)×[0,+∞)→[0,+∞)是关于变量u和s的非增连续函数.对λ∈(0,1), 存在两个常数μ1,μ2>0, 且对任意的(t,u,s)∈[0,b]N0×[0,+∞)×[0,+∞) 有以下不等式成立: f(t,λu,s)≤λ-μ1f(t,u,s), (9) f(t,u,λs)≤λ-μ2f(t,u,s). (10) 注1不等式(9)和(10)分别等价于下列不等式: f(t,λu,s)≥λ-μ1f(t,u,s),∀λ>1; (11) f(t,u,λs)≥λ-μ2f(t,u,s),∀λ>1. (12) 定理8假设(H4)成立,则存在一个常数λ*>0, 使得其对任意的λ∈(λ*,+∞), 边值问题(6)至少存在一个解ω(t), 且存在一个常数0 证明令F=C([ε,b+ε]Nε,R), 并定义一个F的子集P: (13) 事实上,对任意的y∈P, 存在一个正常数0 (14) 再利用定理5、定理6和注1,可得 (15) 令 取 (16) 根据式(14)和(15)可得 (17) 令 故 (18) 令 (19) 对t∈[ε,b+ε]Nε, 利用式(17)和(18),有以下不等式成立: (20) 再通过式(19)和(20)可得 (21) 类似式(14)—(16)的证明过程,可得φ(t),ψ(t)∈P.由式(18)可得 (22) 再由式(19)可知 (23) 考虑到f是非递增的,则通过式(19)、(22)和(23)可得: -λ*f(t′,b + ε-εφ(t′),φ(t′+ε))+λ*f(t′,b + ε-εφ(t′),φ(t′+ε))=0, (24) (25) 根据式(21)—(25)知,ψ(t)和φ(t)是差分边值问题(6)的上解和下解.定义如下函数: (26) 根据性质(H4)和式(26)的定义知F(t,u,s)∶[0,b]N0×[0,+∞)×[0,+∞)→[0,+∞)是连续的. 下证差分边值问题 (27) (28) 当f(t′,b + ε-εφ(t′),φ(t′+ε))≤F(t′,b + ε-εy(t′),y(t′+ε))≤f(t′,b + ε-εψ(t′),ψ(t′+ε))时,有ψ(t)≤y(t)≤φ(t); 当F(t′,b + ε-εy(t′),y(t′+ε))=f(t′,b + ε-εψ(t′),ψ(t′+ε))时,有y(t)<ψ(t); 当F(t′,b + ε-εy(t′),y(t′+ε))=f(t′,b + ε-εφ(t′),φ(t′+ε))时,有y(t)>φ(t). 故f(t′,b + ε-εφ(t′),φ(t′+ε))≤F(t′,b + ε-εy(t′),y(t′+ε))≤f(t′,b + ε-εψ(t′),ψ(t′+ε)).由式(21)、(22)和上式可得 (29) 再由定理5和式(29)可知,对任意的y∈P有 (30) (31) 令z(t)=(φp(b + εα - εφ(t)))-(φp(b + εα - εw(t))), 则有: z(α+ε-2)=(φp(b + εα - εφ(α+ε-2)))-(φp(b + εα - εw(α+ε-2)))=0. 故z(t)≤0, 即(φp(b + εα - εφ(t)))-(φp(b + εα - εw(t)))≤0.事实上,如果定义则根据引理6可得其中K1=0, 因此z(t)≤0. 注意到φp是单调递增的,且b + εα - ε是线性算子,所以有b + εα - ε(φ-ω)(t)≤0.根据式(31)可得φ(t)-w(t)≥0, 因此对任意的t∈[ε,b+ε]Nε有w(t)≤φ(t).同理可得,对任意的t∈[ε,b+ε]Nε有w(t)≥ψ(t).故 ψ(t)≤w(t)≤φ(t),t∈[ε,b+ε]Νε, (32) 且F(t′,b + ε-εw(t′),w(t′+ε))=f(t′,b + ε-εw(t′),w(t′+ε)),t∈[ε,b+ε]Νε.因此,w(t)是差分边值问题(27)的一个正解,y(t)=b + ε-εw(t)是差分边值问题(1)的一个正解.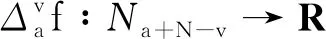


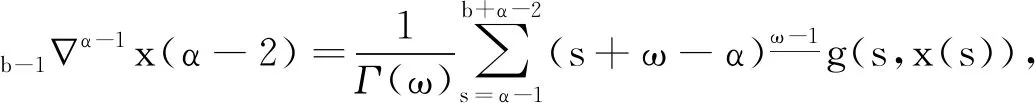



2 主要结果及其证明