采动覆岩导水裂隙主通道分布模型及其水流动特性

曹志国，鞠金峰，许家林

(1.煤炭开采水资源保护与利用国家重点实验室，北京 100011; 2.国家能源投资集团有限责任公司，北京 100011; 3.中国矿业大学 矿山互联网应用技术国家地方联合工程实验室，江苏 徐州 221008; 4.中国矿业大学 物联网(感知矿山)研究中心，江苏 徐州 221008; 5.中国矿业大学 煤炭资源与安全开采国家重点实验室，江苏 徐州 221116)

煤炭地下开采将引起上覆岩层的移动与破坏，从而在覆岩中形成导水裂隙;导水裂隙的产生既为地下水资源流失提供了通道，同时也成为地表生态退化的地质根源[1]。因此，研究揭示覆岩采动破坏后导水裂隙发育、发展的演变规律是评价地下水资源漏失程度、确定保水采煤对策的重要理论依据。

目前有关覆岩导水裂隙演化规律的研究主要集中于导水裂隙带高度的预计和探测[2-7]、开采参数与地质赋存对导水裂隙动态发育的影响规律[6-10]、以及基于上述规律开展的保水采煤理论与技术实践[11-18]等。如，许家林等[2,4]基于岩层控制的关键层理论研究了覆岩导水裂隙随关键层破断运动的动态发育规律，并提出了基于关键层位置的导水裂隙带高度预计新方法，得到了皖北、神东等矿区保水采煤实践的验证。武强等[11]将煤层回采顶板冒落安全性分析和顶板直接充水含水层富水性分析作为顶板涌(突)水危险性分区的重要依据，提出了解决顶板涌(突)水条件定量评价的“三图-双预测法”，有效指导了开滦、台格庙等多个矿区的顶板水害防治实践。王双明、范立民等[12-13]利用煤层顶板含水层等厚线图、顶板隔水层厚度等值线图和导水裂隙带发育高度等值线图这“三图”，对榆神矿区萨拉乌苏组含水层开展了保水采煤的地质分区研究。上述研究极大地丰富了我国保水采煤理论与技术体系，为矿区水资源保护与生态修复作出了重要贡献。但从相关成果可以看出，已有研究多是通过降低覆岩导水裂隙带发育高度以避免含水层被破坏的方式来实现保水采煤，但这一对策在我国西北部的高产高效矿区却难以适用。由于该区域煤层赋存普遍埋藏浅、厚度大、层数多，采煤引起的含水层破坏与地下水流失往往难以避免。因此，从人工干预角度限制导水裂隙的导流能力成为促进含水层生态恢复、实现保水采煤的另一有效途径[18-19]。

有关采动破坏岩体的水渗流特性，已有不少学者[20-24]开展了研究，然而相关研究多是用破碎岩体或峰后破裂岩体的水渗流规律来描述和分析采动岩层导水裂隙的水流动特征。事实上，采动覆岩导水裂隙中除了有岩层受塑性屈服破坏后的压剪裂隙外，还存在着大量因岩层破断回转运动产生的张拉裂隙;这两者在覆岩中的空间分布特征及其发育形态存在着明显差别，且处于裂隙带的拉剪破坏岩体其导水流动状态与垮落带的破碎岩体存在本质区别。因此，单纯以破碎或峰后破裂岩体作为研究对象难以全面、准确揭示覆岩不同区域、不同类型导水裂隙的导流特性。从覆岩导水裂隙带分布的一般特征看，导水裂隙带“马鞍形”凸起区域处于开采边界附近，岩层破断回转形成张拉裂隙，裂隙开度大、过流能力强;对于“马鞍形”下凹区域，处于开采区域中部的压实区，岩层破断块体间的裂隙趋于闭合，过流能力相对较弱;而在“马鞍形”轮廓线侧向偏移位置附近，岩体则受超前支承压力的影响发生塑性屈服，这种环境下产生的压剪裂隙无论在裂隙形态还是过流能力上都与前两者有着明显差异。因此，在覆岩导水裂隙带范围内，必然存在水源漏失的主要流动通道，研究确定导水裂隙主通道的分布规律及其导流特性，对于科学制定导水主通道人工限流的保水对策[18-19]具有重要的指导意义。因此，笔者将基于岩层控制的关键层理论，结合采动覆岩破断形态及其裂隙分布特征，开展导水裂隙水流动特性及其主通道分布模型的研究。

1 覆岩导水裂隙类型划分

导水裂隙是在岩层张拉破坏或受压屈服后产生的，覆岩不同区域岩层所受的应力状态及其自由活动空间不同时，对应产生的裂隙形态和发育程度(或开度)也将有所不同，最终将影响裂隙的导流性能及其对地下含水层的破坏程度。因此，对覆岩导水裂隙的类型进行划分，是开展裂隙导水流动特性分析以及覆岩导水裂隙主通道分布模型构建的前提和基础。

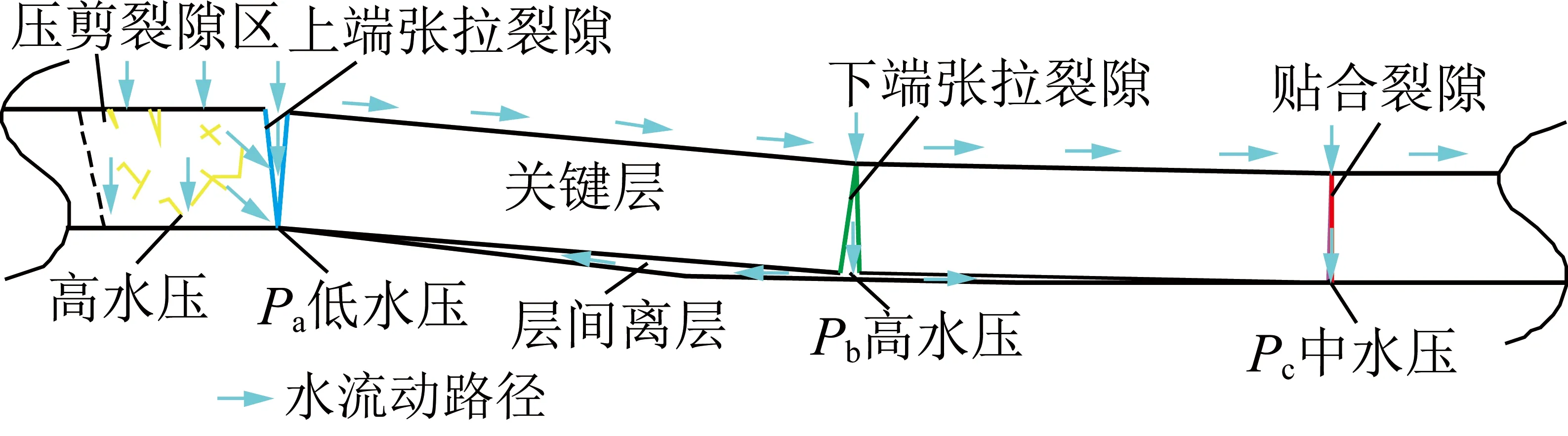
覆岩导水裂隙的形成伴随于岩层的破断运移以及岩体应力的重新分布，在此过程中将存在2种类型的导水裂隙(图1，图中蓝色线条代表上端张拉裂隙，绿色线条代表下端张拉裂隙，红色线条代表贴合裂隙):一类为岩层周期性破断回转运动过程中出现的拉剪破坏裂隙(岩层破断裂隙)，这类裂隙在覆岩中的分布相对均匀，且裂隙间的水平间距近似为岩层的破断步距;另一类为开采边界外侧煤岩体在超前支承压力作用下产生的剪切破坏裂隙(岩层压剪裂隙)，这类裂隙的分布相对杂乱无序，且其分布密度通常要高于前者。

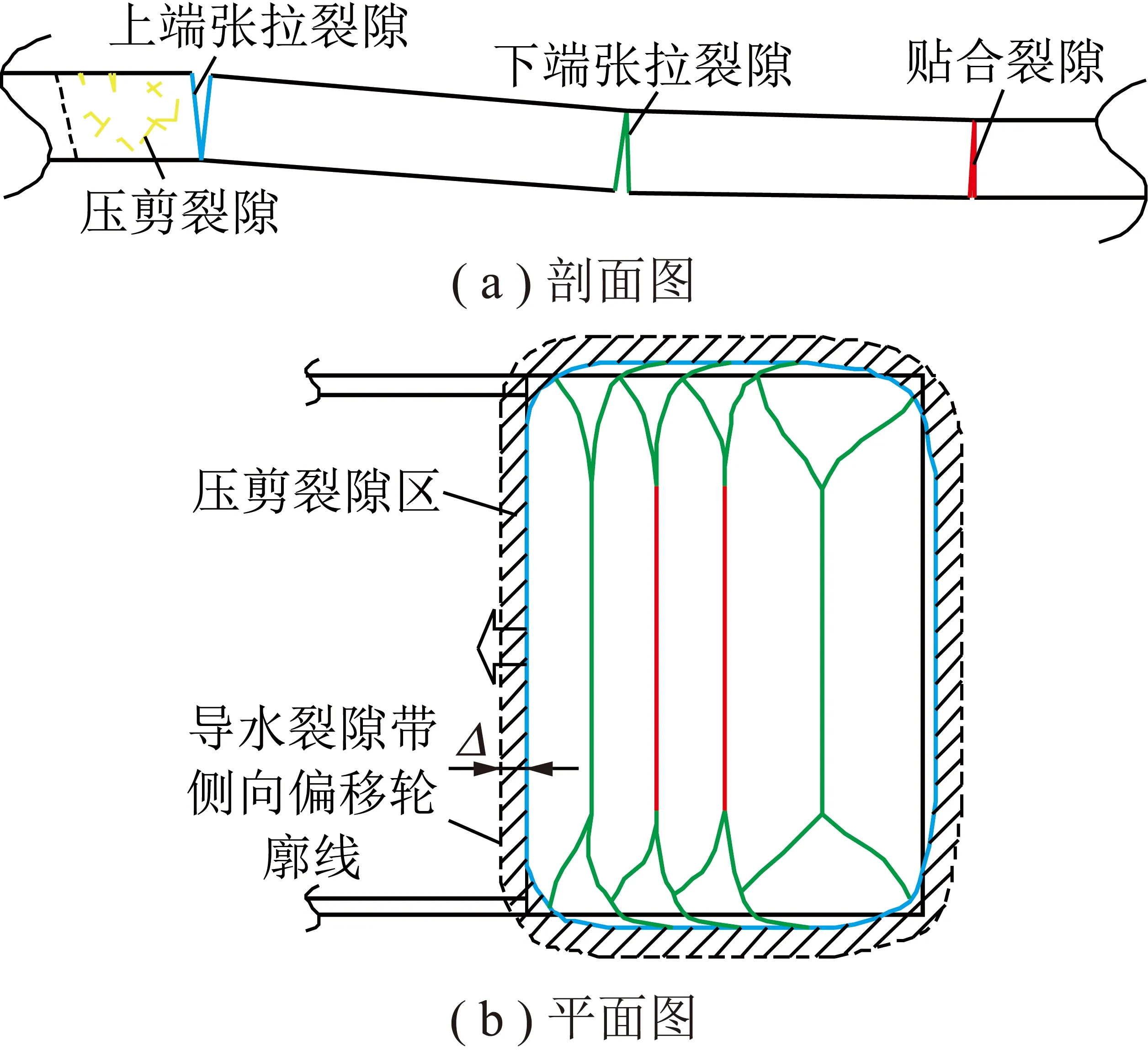
图1 关键层破断运动及其导水裂隙分布示意Fig.1 Breaking movement of KS and the distribution of its water-conducted fracture

对于第1种类型的导水裂隙，受破断岩层在覆岩中不同位置影响，又可分为3种类型，如图1所示。第1，处于开采边界附近的上端张拉裂隙，由于岩层破断块体仅经历一次回转，其回转角始终存在，裂隙剖面呈现类似“楔形”形状;第2，处于开采区域中部压实区的贴合裂隙，由于岩层破断块体已经过双向回转运动，相邻块体间已无回转角差异，裂隙由相邻破断块体水平挤压而成，其外观虽表现为闭合状态，但受相邻裂隙表面形貌及其粗糙度差异的影响，裂隙面并不能完全贴合，裂隙仍具有一定的开度及过流能力;第3，处于开采边界与中部压实区之间的下端张拉裂隙，由于相邻破断块体间回转角的差异，裂隙剖面呈现“倒楔形”形状。

由此可见，覆岩不同区域岩层所受的应力状态及其运移特征不同时，对应其产生的导水裂隙形态和发育程度(或开度)也将有所不同，最终影响到裂隙的导流性能。所以，对不同类型导水裂隙分别建模进行水流动特性的分析显得尤为重要。

2 岩层导水裂隙水流动特性分析

2.1 岩层破断裂隙水流动特性

根据前述分析，岩层破断裂隙可分为上端张拉裂隙、下端张拉裂隙、以及贴合裂隙3种类型。由于这类裂隙是由岩层的破断回转运动产生，其具有规则而特定的发育形态和分布特征，因此，将其与岩体受载状态下的破裂裂隙或破碎岩体裂隙等同视之是不合适的，宜针对单个裂隙建立模型开展水流动特性的分析。假设采动含水层在平面上处于均匀赋存状态，同一平面不同区域的富水状态可视作相同;同时假设岩层为水平分布状态。如此，地下水由采动含水层底界面处向下部岩层中的导水裂隙中流动时，同一裂隙中的水体在同一平面的不同位置处的流动状态基本相同;因而水体在同一裂隙中以垂向流动为主(水平分量可忽略)。基于这一考虑，以图2所示的裂隙剖面形态进行建模分析。

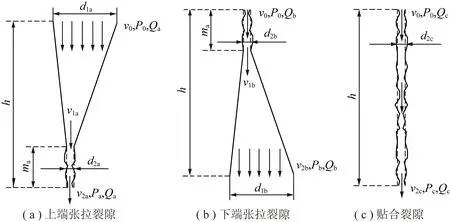
图2 不同破断裂隙断面的水流动特性分析模型Fig.2 Flow characteristics analysis model of fracture section of different broken fractures

2.1.1裂隙导水流态判别

如图2所示，以导水裂隙带范围内处于含水层底界面的邻近岩层为例，假设含水层漏失水体在这3种裂隙入口处的流速和压力相同，分别设为v0和P0;设水体流出裂隙时流速分别为v2a,v2b,v2c，压力分别为Pa,Pb,Pc;通过各裂隙的流量分别设为Qa,Qb,Qc。对于上端张拉裂隙，其过流断面由2部分组成:水流首先通过上端开度为d1a、下端开度为d2a的渐缩通道，其次通过长度为ma、平均宽度为d2a的近似等径通道。其中，d1a与岩层破断块体的回转角β密切相关，可表示为d1a=htanβ，其中h为破断岩层的厚度;d2a为破断块体铰接接触面处的裂隙宽度，考虑到铰接接触面处两侧裂隙面一般难以完全吻合，而处于部分接触、部分“镂空”的状态，因而该处的裂隙宽度按照平均宽度设定。而下端张拉裂隙实质是上端张拉裂隙的倒置形态，两者的进水口和出水口形态正好相反，且d1b的计算方法与d1a相同。贴合裂隙则与前两者在块体铰接接触面处的裂隙类似，也可近似视为等径流动通道，裂隙开度按照张拉裂隙铰接接触面处裂隙的平均开度类似设定。考虑到对于同一岩层而言，各破断块体间是通过同一水平应力挤压接触的，因此可近似视d2a=d2b=d2c。根据上述分析，若取岩层破断回转角为8°[25]，则1 m厚的岩层其上端张拉裂隙的上端开度(或下端张拉裂隙的下端开度)即可达到140 mm。而根据现场曾开展的覆岩导水裂隙注浆封堵的工程实践经验，在注浆骨料粒径1 cm左右的条件下，导水裂隙仍难以有效封堵，可见d2a(或d2b,d2c)值已达到厘米量级。由此推断，此类岩层破断裂隙的导水流态已不再属于渗流范畴，而是管流状态。

为了进一步确定此类裂隙通道的水流动特性，对其雷诺数Re进行了计算。根据非圆通道的雷诺数计算方法[26]，则有

Re=vd/μ

(1)

其中，v为裂隙通道过流速度;μ为水的运动黏度，常温下一般取1×10-6m2/s;d为裂隙通道当量直径，d=4A/χ，χ为裂隙通道的湿周，A为过流断面面积。设裂隙通道的宽度为d′，岩层某一破断裂隙在平面上的延展长度为S，则有

χ=2(d′+S)，A=d′S

因裂隙通道宽度在数值上远小于其平面延展长度，因此χ≈2S。则d=2d′，且式(1)可进一步简化为

Re=2vd′/μ

(2)

由于裂隙通道宽度已达到厘米级别，而从采动破坏含水层中漏失水体的渗流速度一般大于10-4～10-3m/s，因而按照式(2)计算得到的裂隙导流雷诺数至少为1～10;而这正是渗流流态对应雷诺数的上限值。由此进一步证实了岩层破断裂隙的导水流态应属于管流范畴。

2.1.2裂隙导水特性参数

鉴于岩层破断裂隙的导水流态为管流状态，因此，可利用伯努利方程对其水流动特性进行分析。如图2(a)所示，对于上端张拉裂隙，以裂隙出口处对应水平面为基准面，则有

(3)

式中，ρ为水的密度；α1,α2分别为裂隙过流进口和出口处的动能修正系数，一般近似取1;hla为水流通过裂隙后的水头损失(即能量损失)。hla可按v0至v1a水流段的渐缩通道沿程损失hfa和v1a至v2a水流段的等径通道沿程损失hma之和进行计算，两者可分别表示为

(4)

式中，ξa为渐缩通道阻力系数，它与渐缩通道前后的断面比密切相关，由于d2a/d1a一般<0.1，因此ξa取值0.5[26];ma为破断块体铰接接触面长度，可表示为ma=(h-Lsinβ)/2，其中L为岩层破断步距;da,λa分别为v1a至v2a水流段等径通道的当量直径及其沿程阻力系数，其中da根据前节分析可近似为2d2a，λa与雷诺数Rea呈正相关关系，且当Rea<2 000时，裂隙导水流动属于层流，λa根据莫迪图[26]可计算为

λa=64/Rea

(5)

根据式(2)，Rea还可表示为

Rea=2Qa/(μSa)

(6)

其中，Sa为上端张拉裂隙平面延展长度。由现场已有的工程经验可知，一般工作面涌水量不超过2 000 m3/h，因而该裂隙的导水流量也不会超过此极限值。以该极限流量代入式(6)可以发现，250 m宽的常规工作面推进距超过26.5 m时(对应Sa值>553 m)裂隙通道的雷诺数即能<2 000的层流状态临界值。而这一条件一般在基本顶发生初次破断后即可满足。也就是说，岩层破断回转运动产生导水裂隙时对应上端张拉裂隙的导水流动即为层流状态，可以利用式(5)进行λa值的计算。由此式(4)可进一步表示为

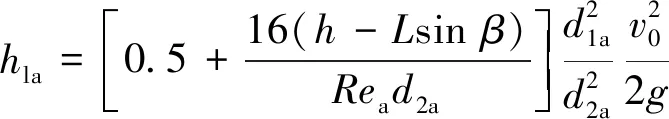
(7)

代入式(3)，上端张拉裂隙导水流动的伯努利方程可表示为

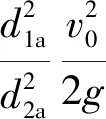
(8)

结合图1(b)，对应裂隙的导水流量可表示为

Qa=v0d1aSa=2(B+Y)v0d1a

(9)

式中，B为工作面宽度;Y为岩层发生破断区域沿工作面推进方向的长度。

同理，可对下端张拉裂隙以及贴合裂隙对应的导水特性参数进行求解。

对于下端张拉裂隙，令其雷诺数为雷诺数Reb，其过流水头损失同样分为2个部分:

考虑到d2b/d1b值较小而接近于0，因此下端张拉裂隙的过流总水头损失可简化为

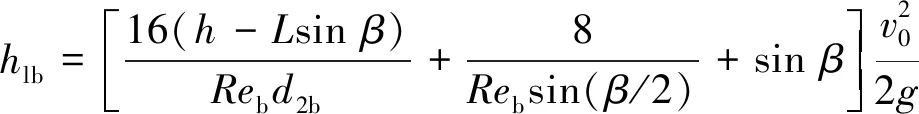
(10)

对应伯努利方程为

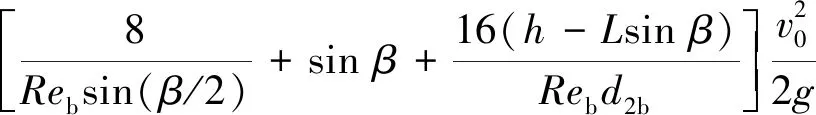
(11)

裂隙的导水流量为

Qb=[2(B-Lh)+4nLh]v0d2b=2(B-

Lh+2ωY)v0d2b

(12)

其中，n为岩层发生周期破断的次数(含初次破断);Lh为岩层发生“O-X”破断在开采边界处的弧形三角块沿工作面倾向的长度;ω为Lh与岩层周期破断距的比值。对于贴合裂隙，令其雷诺数为雷诺数Rec，其过流水头损失为

(13)

对应伯努利方程为

(14)

裂隙的导水流量为

Qc=(n-2)(B-2Lh)v0d2c=(ωY/Lh-

2)(B-2Lh]v0d2c

(15)

2.2 岩层压剪裂隙水流动特性

对于超前煤岩体在支承压力作用下产生的压剪裂隙的水流动特性，其实质上岩石峰值应力后的水渗流问题。由于岩体内裂隙的分布杂乱无序，难以对每个裂隙分支分别进行建模分析;因此，许多学者多选择某一区域的裂隙岩体开展水渗流特性的试验测试与理论建模工作[21-24,27-29]，取得了许多有益成果。相关研究指出，该类裂隙岩体水流动特性呈现Forcheimer型非Darcy渗流特性，其渗透率k一般处于10-11～10-8cm2的量级。相比上述岩层破断裂隙，其导流能力已大幅降低。根据Forcheimer提出的二项式方程，其渗流压力梯度P与渗流流量Q满足

(16)

式中，φ为非达西因子;σ为水的动力黏度，常温下一般取值1 mPa·s。由此可根据式(16)确定其渗流流量的表达式

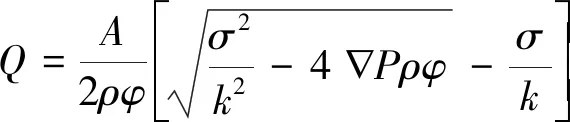
(17)

式中,过流断面面积A根据图1(b)表示为A=2Δ(B+Y)，其中Δ为压剪裂隙在岩层平面上的分布宽度，也就是覆岩导水裂隙带轮廓线在该岩层的侧向偏移位置距岩层破断裂隙的水平距离(图1(b))。

而对于岩层压剪裂隙的其他相关水渗流特性的描述，考虑到已有许多学者开展了丰富研究，本文就不再赘述。

2.3 不同类型导水裂隙的水流动特性对比

根据前述各种裂隙类型对应的导流参数，可对不同类型导水裂隙的水流动特性进行对比分析。考虑到采动岩层的破断运动受控于覆岩关键层[30]，因而导水裂隙的发育也与关键层的破断运动密切相关。因此，本节专门选取覆岩关键层中产生的导水裂隙进行水流动特性的对比分析。

2.3.1裂隙导水流量

对于岩层破断裂隙的3种类型导水裂隙，其导水流量的差异主要在于裂隙的平面延展长度及其导流进口处的裂隙开度。其中，下端张拉裂隙和贴合裂隙的进流口开度可近似视为相等，即d2b=d2c，而上端张拉裂隙的进流口开度d1a与前两者一般存在100倍的差异(d1a值一般为分米或米级，而d2b,d2c值一般为厘米或毫米级)。即d1a∶d2b∶d2c≈100∶1∶1。而对于各裂隙的平面延展长度，主要受工作面开采参数和岩层破断参数的影响;其中B,Lh，ω值受开采条件影响其变化相对较小，岩层发生破断区域的走向长度Y值受工作面推进距变化影响可由几百米至几千米，幅度相对较大。为了便于对比各类裂隙S值之间的差异，按照现场工程一般经验和实测结果，取工作面宽度B为250 m;关键层弧形三角块长度Lh一般为30～50 m，取值40 m;关键层周期破断距一般为10～25 m，因而ω一般为2～5，本次取值3.5。由此根据式(9),(12),(15)可得到关键层3种破断裂隙平面延展长度与工作面推进距的关系曲线，绘制如图3所示。由图3可以看出，在目前国内已有工程案例5 000 m推进距的最大值条件下，无论工作面推进距如何，下端张拉裂隙和贴合裂隙的S值基本相同，且其值一般为上端张拉裂隙对应S值的4～7倍。由此，综合3种裂隙的进流口开度比值，它们的裂隙导流流量的比值为Qa∶Qb∶Qc≈100∶(4～7)∶(4～7)。说明上端张拉裂隙相较于其他两种破断裂隙其导水流量明显偏大。

图3 3种破断裂隙平面延展长度对比曲线Fig.3 Contrast curves of the plane extension length of three different types of broken fracture

而对于岩层压剪裂隙的导水流量，由式(17)可知，除了与在关键层破坏区域的分布面积A和渗流压力梯度有关外，还与裂隙的渗透率k及其非达西因子φ密切相关。与上述3种类型的岩层破断裂隙类似，A的取值主要受Y的影响而有较大变化幅度。类似地，令工作面宽度B=250 m;压剪裂隙在岩层平面上的分布宽度Δ一般为5～25 m，取值15 m;则A=7 500+30Y。根据已有研究结果[21-24,27-29]，该类裂隙的非达西因子φ一般为1012～1015m-1量级;若取φ=5×1013m-1，渗透率k取值5×1013m2，水的密度取1 000 kg/m3，则式(17)可进一步简化为

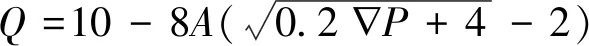
(18)

含压剪裂隙岩体的水压梯度一般处于104～106Pa/m量级[21-23]，而对于岩层破断裂隙进口处的初始水流速度v0，实际是含水层受采动破断后其漏失水体涌出含水层而进入其与下部岩层之间层理空间时的瞬时速度，其值一般为10-4m/s量级[31]。以压剪裂隙中104Pa/m的压力梯度量级为例，可对这2类4种裂隙的导水流量与工作面推进距的关系曲线绘制如图4所示,下端张拉裂隙与贴合裂隙的曲线处于重叠状态(3种破断裂隙的进流口开度d2a,d2b,d2c分别取值100,1,1 cm)。

图4 不同类型裂隙的导水流量对比曲线Fig.4 Contrast curves of the water flow as water pass through different types of water-conducted fracture

由图4可以看出，上端张拉裂隙的导水流量显著高于其他3种裂隙对应流量，下端张拉裂隙和贴合裂隙的导水流量基本接近，且导水流量次之;而压剪裂隙的导水流量则是其中最小的，约为下端张拉裂隙(或贴合裂隙)导水流量的0.2～0.3倍，但仅为上端张拉裂隙导水流量的0.015倍。

2.3.2裂隙导水流动损耗

对于岩层破断裂隙的3种类型导水裂隙，由式(7),(10),(13)可知，其导流后的水头损失主要与雷诺数以及裂隙发育形态尺寸有关。考虑到d1a与d2b,d2c近似相等，且d1a近似为d2a的100倍，因此有

d1a∶d2b∶d2c=100∶1∶1

所以

(19)

(20)

由于d1c值一般为10-3～10-2m，Rec值不超过2 000，因此，式(20)也是>0的，即hlc>hlb。所以有

hla>hlc>hlb

(21)

在裂隙出口处，3种裂隙对应的水流速度比值为

(22)

由此根据式(8),(11),(14)所示的伯努利方程可知，3种裂隙出口处的水压有

Pa

(23)

综上分析，上端张拉裂隙导流的水头损失和水压衰减最大，但出口处的水流速度递增最快;而下端张拉裂隙导流的水头损失和水压衰减最小，但出口处的水流速度递减最大;贴合裂隙导流的相关特性参数变化趋势介于上述两者之间。

而对于水体在压剪裂隙中的渗流，其导水流动损耗相对较小，一般呈现渗流速度缓慢递增、水压缓慢递减的状态，且两者的变化幅度基本一致;仅当渗流水体进入其他类型裂隙(如上端张拉裂隙)赋存区域时，上述渗流速度的递增和水压的递减才会出现突变，并造成流动损耗的大幅提升[21-24,27-29]。由于它与岩层破断裂隙分属两种截然不同的导水流动状态，尚难以对其两者的流动损耗情况进行对比。

2.4 讨 论

(1)为了研究分析的简便，本章是以覆岩中典型的岩层关键层作为研究对象开展不同类型导水裂隙水流动特性对比分析的。但受覆岩中各岩层物理、力学特性差异的影响，不同岩层中各类导水裂隙的发育参数与本章中所述关键层的相关参数可能有所不同(如裂隙的平面延展长度、裂隙开度等)，从而可能影响到该岩层中各类裂隙相关导水流动参数的绝对值。例如，覆岩中某些软弱岩层跟随关键层发生板“O-X”破断时[25]，其破断块体并不一定如图1(b)所示在平面上呈现一个整体，而有可能在倾向上也发生几次破断，由此该岩层对应贴合裂隙的平面延展长度将比图1(b)所示增大数倍。但受岩层破断运移空间总量的限制，裂隙平面延展量的增多必然带来单一裂隙开度的减小，从而裂隙的最终导流参数值难以出现倍增的现象。所以，对于同一岩层而言，其发育的各类裂隙之间导流特性的相互差异是基本不变的。

(2)采动漏失水体经由导水裂隙穿越某一岩层上下界面后，受相邻岩层间离层空间发育的影响，从各区域裂隙流出的水体会在离层区重新达到另一流动状态;也就是说，进入下一岩层裂隙进口处的水流动状态已不再等同于上一岩层对应裂隙出口处的水流动状态。尤其是在水体流动穿越开采边界附近对应关键层上下界面后，由于关键层底界面离层发育最为明显且空间较大[30,32]，裂隙导水流动特性的重置现象会更为突出。从这个角度看，采动漏失水体由含水层流至井下采出空间的水流动过程可能并非连续的;也进一步说明，将覆岩导水裂隙带内岩层单纯按峰后或破碎岩体作为一个整体来研究其导水流动特征和规律是不合适的。

3 采动覆岩导水裂隙主通道分布模型

由前述分析可知，采动覆岩不同区域因其不同的受力环境和破断运移特征而产生了不同形态的导水裂隙，从而造成了覆岩不同区域明显差异的导水流动特征。结合上述研究结果，可对采动覆岩导水裂隙主通道分布进行模型构建与区域划分。

3.1 导水裂隙主通道分布模型

根据2.3节不同类型导水裂隙的水流动特性对比分析结果可知，处于开采边界附近的上端张拉裂隙，无论相较于同类型的破断裂隙(下端张拉裂隙、贴合裂隙)还是导水裂隙带侧向偏移处的压剪裂隙，它的裂隙过流能力都明显偏高;主要表现为裂隙进流口开度大、导水流量高、出口流速快等特征。

而从同一岩层不同导水裂隙之间的导水流动路径看，各裂隙导流后受水压差异的影响，各自间又存在一定的水补给作用，如图5所示。由式(24)可知，上端张拉裂隙出水口处于较低的水压状态，而处于其两侧的压剪裂隙区和下端张拉裂隙出水口均呈现相对较高的水压状态;由此在水压梯度作用下，两侧的裂隙导流水体将会向上端张拉裂隙处汇聚。具体表现为:压剪裂隙区的高压水体沿岩层内的压剪裂隙向上端张拉裂隙通道内补给，而下端张拉裂隙出水口的高压水体则沿岩层之间的离层空间向其出水口补给。而由于下端张拉裂隙与贴合裂隙出水口处的水压差异相对偏低，且两者之间的水径流补给通道相对前者的离层空间较小(贴合裂隙区处于岩层压实状态，层间离层难以发育)，因而，由下端张拉裂隙出水口向贴合裂隙区补给的水流量相对前者将明显偏小。

图5 关键层各区域导水裂隙导流路径示意Fig.5 Flow path of the water when passing through the water-conducted fracture in different area of the KS

由此可见，无论是从裂隙的导水流量、流速还是从裂隙的导流路径来看，含水层受采动破坏后引起的井下工作面涌水量大多是由压剪裂隙区和下端张拉裂隙之间的裂隙导流而来。依据此，可根据上端张拉裂隙的发育区域进行覆岩导水裂隙主通道分布区域的划分。

由于煤系地层中各岩层在岩性、厚度、力学强度以及受力环境等方面都存在较大差异，若对采动覆岩各岩层都进行上端张拉裂隙发育位置的确定，将存在较大难度。考虑到岩层的破断运移直接受控于覆岩关键层[30]，因此可根据关键层的破断运动特征及其裂隙发育规律来探寻导水裂隙主通道的分布范围。基于上述思路，考虑工作面开采处于充分采动状态，构建了如图6所示的覆岩导水裂隙主通道分布剖面模型。由图6可以看出，导水裂隙主通道分布区域位于开采边界两侧，并近似以导水裂隙带内各层关键层在开采边界处的破断距为宽度，形成的类似梯形的区域。图中lc1,lc2分别为关键层1,2的超前破断距，L1,L2分别为两关键层在开采边界处的破断距，且在倾向剖面上该破断距为关键层弧形三角块破断长度，在走向剖面上则为关键层的周期破断距(对应终采线处的开采边界)或初次破断距的一半(对应开切眼处的开采边界)。也就是说，若覆岩导水裂隙带高度发育至某关键层i底界面，则导水裂隙主通道分布区域的一侧边界为该关键层直至关键层1超前破断位置的连线，而另一侧边界则为导水裂隙带内关键层超前破断块体末端连线，并从关键层i-1相应位置按岩层破断角α向上延伸至导水裂隙带顶界面。

图6 采动覆岩导水裂隙分区及其主通道分布剖面模型Fig.6 Partition of water-conducted fracture in overlying strata and the distribution model of main channel

3.2 讨 论

(1)利用导水裂隙主通道分布模型可科学指导“覆岩导水裂隙人工限流”保水对策的实施。现场开采实践表明，在我国西北部等煤炭资源丰富的高强度开采矿区，覆岩导水裂隙带常易直接发育至地表，单纯依靠限制导水裂隙发育的方式进行保水采煤往往难以实现，采取人工干预措施对覆岩中已形成的导水裂隙实施人工修复(如注浆封堵)成为解决这一难题的有效途径[18-19]。针对这一措施，现有的对策往往对采动覆岩所有区域的导水裂隙都考虑进行人工修复，这在理论上虽然能彻底隔绝地下水的漏失通道，但实际实施时却存在难度大、施工复杂、成本高等缺点。所以，若能依据图6所示的导水裂隙主通道分布模型，集中对导水裂隙主通道区域采取注浆封堵等人工干预修复措施，这无疑能将采空区大部分涌水流量阻截在导水裂隙之外;地下水仅能从导水裂隙带主通道分布区域之外的其他小流量裂隙渗漏。如此虽未能彻底消除井下涌水，但却大大提高了实施效率和便利程度，不失为导水裂隙人工限流的一项有效保水对策。

图7 邻近工作面回采对导水裂隙主通道分布的影响Fig.7 Influence of the mining of nearby face to the main cha- nnel distribution on water-conducted fracture in overlying strata

(2)导水裂隙主通道分布模型合理解释了现场开采实践中常出现的回采工作面涌水对邻近老采空区涌水的“袭夺”现象(即回采工作面涌水会减小邻近已采采空区原有涌水量)。设单一工作面开采后(充分采动)覆岩导水裂隙主通道分布平面图如图7(a)所示，当邻近工作面回采时，回采区域对应区段煤柱实际已处于两工作面采空区的中部压实区(区段煤柱一般极易发生失稳)，从而该区域对应已采工作面覆岩导水裂隙主通道将会消失，由此造成了已采工作面采空区涌水量的减少;且随着邻近回采工作面的不断推进，已采工作面采空区涌水量会因导水裂隙主通道分布区域的逐步减小而不断降低，而回采工作面涌水量则随之增高，如此才出现了两工作面采空区涌水量的“袭夺”现象。

4 结 论

(1)根据岩层采动导水裂隙产生原因的不同，将其划分为2类4种:一类为开采边界外侧煤岩体受超前支承压力作用而产生的峰后压剪裂隙，另一类为岩层周期性破断回转运动产生的拉剪裂隙。后者根据不同区域岩层破断块体回转运动状态的差异又可分为3种类型:开采边界附近的上端张拉裂隙和下端张拉裂隙，以及中部压实区的贴合裂隙。

(2)超前煤岩体峰后压剪裂隙的导水流态属于非达西渗流，其导水流动常呈现渗流速度缓慢递增、水压缓慢递减以及渗流流量小等特征;仅当渗流水体进入其他类型裂隙赋存区域时，其水流动状态才会出现突变，并造成流动损耗的大幅提升。

(3)岩层破断运动形成的拉剪裂隙，因其导水雷诺数相对偏高，属于管流范畴的导水流态。受其分属的3种类型导水裂隙不同发育形态的影响，各种裂隙呈现明显不同的导水流动特征。上端张拉裂隙导流的水头损失和水压衰减最大，但流速递增最快、流量最高;而下端张拉裂隙导流的水头损失和水压衰减最小，但出口流速递减最大;贴合裂隙的导流特性参数化趋势则介于上述两者之间。

(4)地下水经由导水裂隙穿越某一岩层上下界面后，受相邻岩层间离层空间发育的影响，各区域裂隙流出的水体会在离层区重新达到另一流动状态;尤其是在水流穿越开采边界附近对应关键层上下界面后，由于关键层底界面离层发育最为明显且空间较大，裂隙导水流动特性的重置现象会更为显著。可见，采动漏失水体由含水层流至井下采出空间的水流动过程可能并非连续的。

(5)根据岩层破断形成的上端张拉裂隙的发育区域进行了覆岩导水裂隙主通道的分布模型的构建;导水裂隙主通道分布区域位于开采边界两侧，且是以裂隙带内各关键层在开采边界附近的超前破断位置及其破断距设定边界而形成的类梯形区域。该模型为合理实施导水裂隙人工限流的保水采煤对策以及人工限流区域的科学选取提供了依据，同时也合理解释了现场采煤实践中常出现的回采工作面涌水对邻近采空区涌水的“袭夺”现象。

本文的研究只是基于采动岩层破断运动及其裂隙发育特征而构建形成的一个理论模型，限于篇幅，尚未用实测或实验数据对其进行验证，后续将另撰他文开展更深入的研究。