破裂孤子方程的精确解*
蒋桂凤
(台州学院 电子与信息工程学院,浙江 临海317000)
0 引言
随着社会的进步和科技的发展,在物理学、神经学、航空学等多种学科领域,非线性偏微分方程的应用越来越广。非线性系统在展现复杂多变的自然现象中比线性方程更加精准,研究也更有价值。为了精确地描述事物的本质特征,研究非线性偏微分方程的精确解的解法也得到了很多的发展,许多非线性方程得到了一些精确解[1-6]。但由于非线性演化方程求解的困难,所以求解非线性方程的精确解还没有系统的方法。
本文利用改进的Kudryashov 方法,选取适当的一阶常微分方程来探求(2+1)维破裂孤子方程及(2+1)维Bogoyavlenskii"s 广义破裂孤子方程的精确解。
1 研究破裂孤子方程的意义与方法
1.1 研究破裂孤子方程的意义
在自然界中存在着大量的折叠现象,流形中的气泡、海浪等都是折叠波,这些现象都可以用破裂孤子方程来描述。近些年,该方程已被应用到许多领域,破裂孤子方程的解的研究也成为了热点。
许多研究者用各种方法研究破裂孤子方程,如傅海明、戴正德应用扩展F 展开法[7]、刘玉堂与刘玉珍利用对称法[8]、张琳琳与刘希强应用李群分析法[9]、张解放、郭冠平用齐次平衡法和推广的hirota 双线性方法[10]、套格图桑与斯仁道尔吉用新辅助法[11]等。通过这些方法,破裂孤子方程的一些精确解被得到。
2012 年,Kudryashov 方法由俄罗斯数学家Nikolay A.Kudryashov 提出,目前该方法已被许多人所应用,得到了一些偏微分方程的解[12-13]。
本文利用改进的Kudryashov 方法,引进简单方程的方法,对研究的破裂孤子方程进行化简,求出一系列的新解,这对于研究折叠波等有重要意义。
1.2 改进的Kudryashov方法——构造一阶常微分方程,求破裂孤子方程的精确解
若一个偏微分方程经过行波变换化为常微分方程
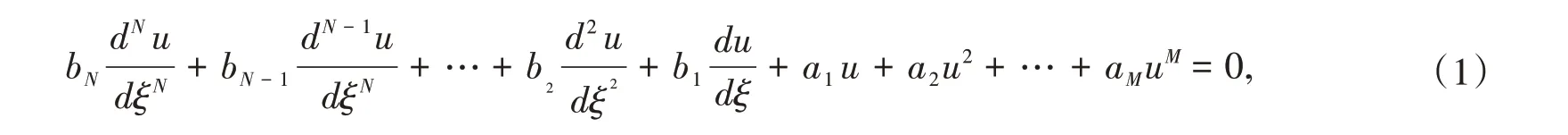
则可以令方程(1)具有如下形式的精确解[14]:
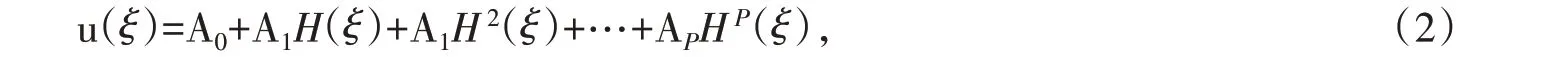
其中H(ξ)满足容易求解的一阶常微分方程——Bermoulli 方程:

这里a,b 是常数。Bermoulli 方程是在化工中的流体输送过程中最基本的方程之一,它是在连续稳定的流体状态下,能揭示流体流动时能量的守恒定律。
为了求得(1)的解,我们把(2)、(3)代入(1)得到以下的方程:
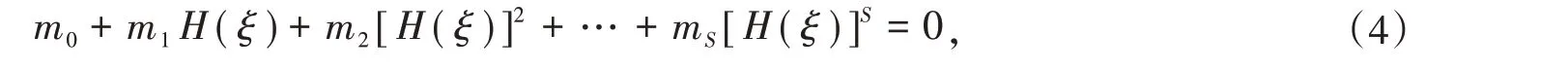
其中S 为整数。
当取方程(4)的系数都为零,即m0= m1= m2= … = mS= 0 时得到一个代数方程组,求解就可以得到相应的方程(1)的解。
为了确保得到的代数方程组中的每一个方程至少有两项,我们对(4)的非线性项产生的最高次数与最高阶导数产生的最高次幂进行平衡,得到等式:

齐次平衡法是求非线性发展方程解的一种有效方法,现在,对于流体、弹性体等变形体的研究,很多都应用了齐次平衡方法[15-16]。
2 两类非线性微分方程的精确解
2.1 (2+1)维破裂孤子方程的精确解
1976 年Calogero 和Degasperis 提出了(2+1)维破裂孤子方程[17]:

它描述了非线性波方程的长波沿x 轴传播,黎曼波沿y 轴传播的相互作用。
我们假设方程(6)的精确解为:

则方程(6)化为

对方程(8)积分,取积分常数为零,得

令u" =φ(ξ)则有

由1.2 内容知,平衡等式(5),得到

所以当取K=2 时,有P=2,因此方程(10)具有如下的解:

其中H(ξ)满足一阶常微分方程

把(11)及(12)代入方程(10),再取H(ξ)i(i=0,1,2,3,4)的系数都为零,得到如下代数方程组:

解方程组(13),得到

所以方程(10)的解为

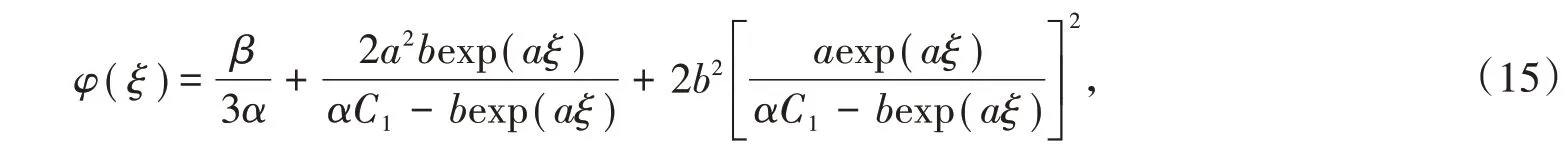
其中C1为积分常数。
因此(2+1)维破裂孤子方程(6)的解为:
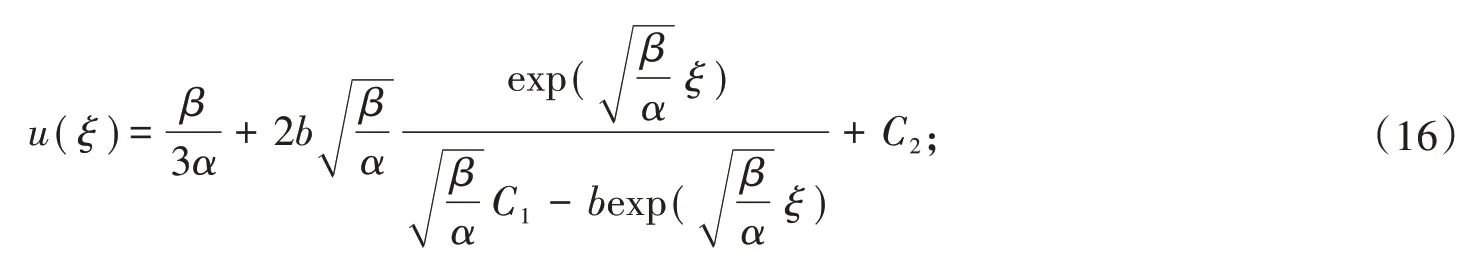
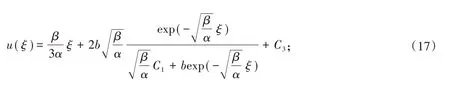
其中ξ = x + αy + βt,C2,C3是积分常数。
2.2 (2+1)维Bogoyavlenskii"s广义破裂孤子方程的精确解
自从O.I.Bogoyavlenskii 提出了(2+1)维破裂孤子方程的相伴AKNS 谱系以来,破裂孤子方程的研究受到了许多的研究者关注。本文研究(2+1)维Bogoyavlenskii"s 广义破裂孤子方程:

与2.1 相同,我们假设方程(18)的解为:

则方程(18)就化为

积分两次,取积分常数为零,得到
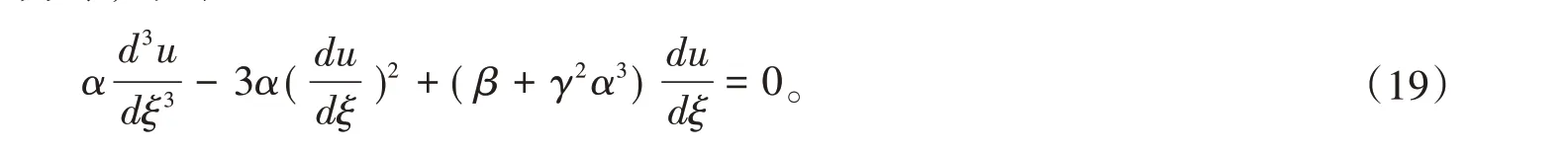
令u" = φ(ξ)则有

同样由平衡等式(5)可知,当取K=2 时,有P=2,因此方程(20)具有如下的解:

其中H(ξ)满足方程
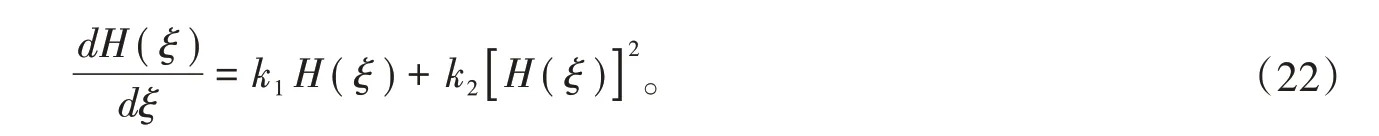
与2.1 方法类似,把(21)及(22)代入方程(20),再取H(ξ)i(i=0,1,2,3,4)的系数都为零,可求得
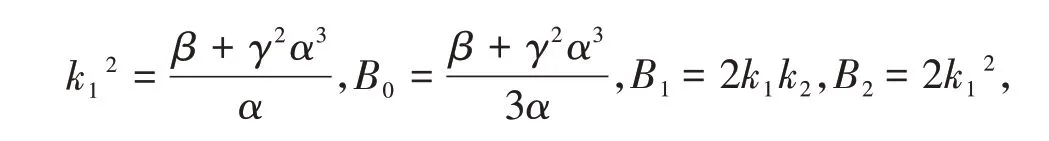
所以方程(20)的解为

即

其中C4为积分常数。
因此(2+1)维Bogoyavlenskii"s 广义破裂孤子方程的解为:
(1)当k1= h >0 时,

(2)当k1= -h <0 时,

其中ξ = x + αy + βt,C5,C6是积分常数。
3 结语
总之,非线性偏微分方程是描述客观事物非线性演化过程的数学物理方程,几乎不存在通用的方法研究方程的解。本文借助已知能求解的常微分方程,利用改进的Kudryashov 方法,得到了(2+1)维破裂孤子方程和(2+1)维Bogoyavlenskii"s 广义破裂孤子方程的许多精确解。这种方法可以用来研究更多的非线性偏微分方程问题,得到它们的解。

