数学文化体现在立体几何专题中的教学研究

【摘要】2017年《高中数学课程标准》提出了“六大数学核心素养”即数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析,它是五大基本能力和两个意识的延续和深化.2017年高考数学考试大纲增加了对“数学文化”的考查,体现了数学学科对学生核心素养的考核.为了适应新课改要求,本文针对高中阶段立体几何专题体现数学文化的教学进行研究.
【关键词】新课改;数学文化;核心素养;立体几何
【基金项目】本文是四平市“十三五”规划课题《基于新高考改革背景的高中数学核心素养培养研究》阶段性成果,课题批号:JL-SP-ZT-GK-015.
2017版《普通高中数学课程标准》将核心素养作为贯穿始终的“灵魂”,对数学的六大核心素养内容进行了系统的阐述.2018年全国II卷理科数学试卷,以思维为核心,考查学生的数学核心素养,充分体现了数学学科特点.这就要求教学中要从数学学科本质观出发,凝练核心素养;以核心素养为纲,选择、构建课程内容;以核心素养为目标,改革教学方式;结合核心素养和学科内容,设计学业质量标准.加强数学文化的教育,就是为了提升数学核心素养.
一、数学文化体现在高考中的主要问题
2018年高考试题在考查数学知识的同时,也渗透数学文化的考查,如全国Ⅱ卷理科第10题借助于古希腊数学家希波克拉底所研究的几何图形(月形定理)考查了几何概型;北京卷理科第4题(文科第5题)关注了我国明代朱载堉对十二平均律的重要贡献.
数学文化融入高考,能够使数学文化进入课堂,既能落实新课程标准的要求,又能激发学生学习数学的兴趣.从文化角度来关注数学,重视数学价值,能持续提升教师和学生的数学素养,也能增强学生用理性思维理解事物的视野.学生只有了解了数学的价值,才能自觉学习数学,学好数学.
高考全国卷在2013年到2017年间,在全国Ⅰ卷或全国Ⅱ卷中相应设置了一些数学文化的试题.从题型上看主要以小题的形式出现在选择题或填空题里面;从考查的知识点上,以我国经典数学名著《九章算术》《数书九章》《算法统宗》和《算数书》中的问题为背景的文化试题.
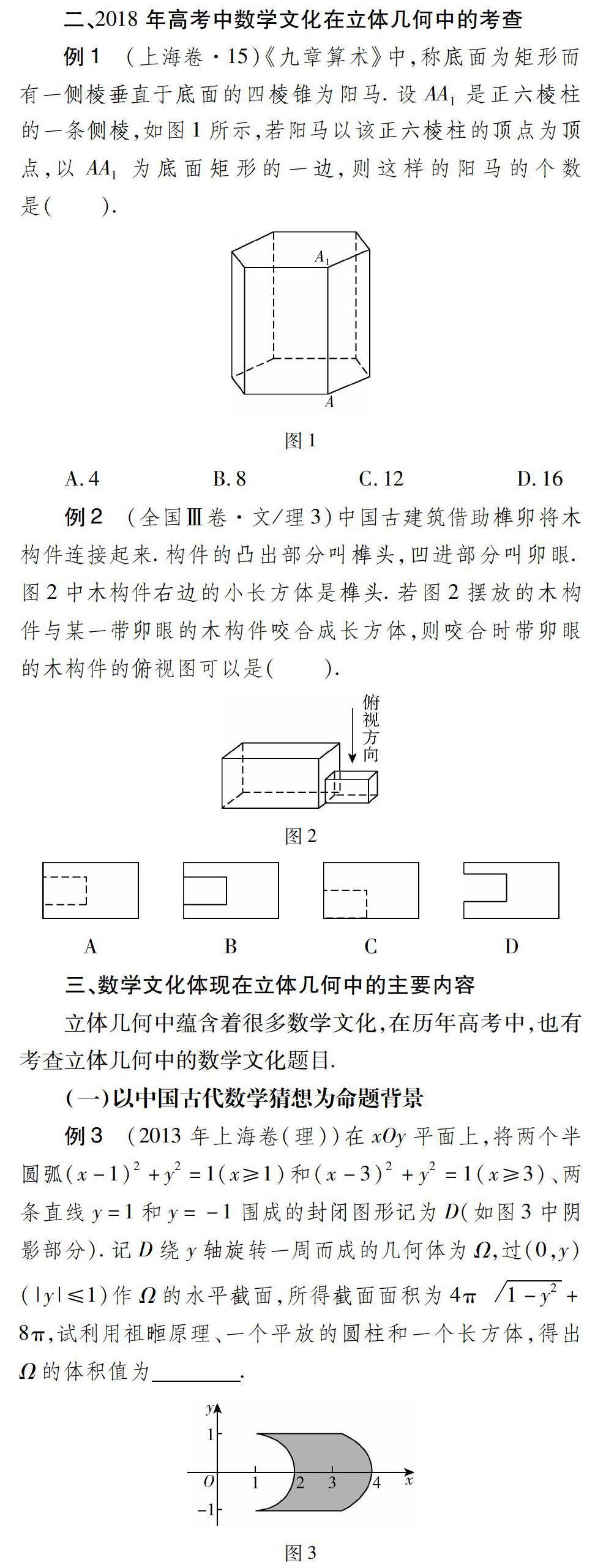
二、2018年高考中数学文化在立体几何中的考查
例1 (上海卷·15)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱,如图1所示,若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马的个数是( ).
A.4
B.8
C.12
D.16
例2 (全国Ⅲ卷·文/理3)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼.图2中木构件右边的小长方体是榫头.若图2摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( ).
三、数学文化体现在立体几何中的主要内容
立体几何中蕴含着很多数学文化,在历年高考中,也有考查立体几何中的数学文化题目.
(一)以中国古代数学猜想为命题背景
例3 (2013年上海卷(理))在xOy平面上,将两个半圆弧(x-1)2+y2=1(x≥1)和(x-3)2+y2=1(x≥3)、两条直线y=1和y=-1围成的封闭图形记为D(如图3中阴影部分).记D绕y轴旋转一周而成的几何体为Ω,过(0,y)(|y|≤1)作Ω的水平截面,所得截面面积为4π1-y2+8π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为.
(二)以中国古代数学名著为命题背景
《九章算术》是我国古代数学名著,多次出现在高考试题中,比如,2011年、2012年的湖北高考卷,2015年的全国高考Ⅱ卷,等.另外,《算数书》《数书九章》等名著都曾出现在高考数学试题中.
例4 (2015年新课标Ⅰ卷文、理6)《九章算术》是我国古代内容极为丰富的数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米,米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( ).
A.14斛
B.22斛
C.36斛
D.66斛
例5 (2012年湖北卷理10)我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式d≈3169V.人们还用过一些类似的近似公式.根据π=3.14159…判断,下列近似公式中最精确的一个是( ).
A.d≈3169V
B.d≈32V
C.d≈3300157V
D.d≈32111V
例6 (2015年湖北卷文17)《九章算术》中,将底面为长方形且有一条侧棱與底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图5所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.
(1)证明:DE⊥平面PBC.试判断四面体EBCD是否为鳖臑.若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.
(2)记阳马P-ABCD的体积为V1,四面体EBCD的体积为V2,求V1V2的值.
四、数学文化体现在立体几何中的教学策略
数学文化的意义还不仅在于知识本身和它的内涵,还在于它的应用价值,尤其是立体几何,应用价值更明显.在教学中应该加强数学与实际生活的联系,增强数学的应用性,让学生体验到数学文化的价值就在于生活的各个领域中都要用到数学.
1.创设问题情境,激发学生学习兴趣.兴趣是最好的老师.授课前,创设每个数学专题的数学情境,从而激发学生探求新知的欲望,提高学习效果.比如,在有限制条件排列时,对本班学生进行分组,提出不同的问题,让各个小组研究出各自的解决办法,进而归纳出解决有限制条件排列的特殊元素位置(优选法)、相邻问题(捆绑法)、不相邻问题(插空法)、定序问题(消序法或留空法)等方法.这样不仅发挥了学生的主动性,也激发了学生的学习兴趣,增强了课堂教学效果.
2.注重解决问题,提升学生实践水平.引导学生将数学融入日常生活中,比如,在讲到充要条件时,让学生们设计不同电路,来验证什么是充分不必要、必要不充分、充分必要、既不充分也不必要条件,这样不但使学生直观理解充要条件概念,更能提高学生的动手能力.在讲到正、余弦定理应用时,把班级学生分成几个小组,测教学楼的高度,这样既加深了对正、余弦定理的理解,又能提高学生的解决问题、将理论应用于实践的能力.
3.改进教学方式,增强学生自主能力.在教学中,要改变以往教师教、学生学的教学方式,发挥学生的自主学习能力.鼓励学生自己去学习、研究数学文化.比如,让他们通过阅读数学趣味故事、数学家成长故事、数学史等,开阔学生的视野.在班级文化墙上开展数学手抄报、上台讲数学故事等,让学生自己独立完成教材上的数学实习作业,通过这些来拓展学生的数学学习能力.
【参考文献】
[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
[2]丁益祥.高考内容改革背景下的高中数学教学策略[J].中国考试,2017(1):48.
[3]陈雪莲,王新宏.高考“数学史料题”的赏析及启示[J].教学月刊(中学版),2016(5):55-59.
[4]冯亮.数学文化知识体现在数列专题中的教学研究[J].数学学习与研究,2019(3):67-68.
[5]童其林.高考数学核心素养解读[M].哈尔滨:哈尔滨工业大学出版社,2017.
[6]华文娜.2018年上海数学高考试题浅析[J].中学数学,2019(1):35-36.

