地铁车辆辅助变流器的气动噪声研究

丁 杰 ，张 平 ，刘海涛 ，李 华 ，赵清良 ，王永胜

（1. 湘潭大学土木工程与力学学院，湖南 湘潭 411105；2. 株洲中车时代电气股份有限公司技术中心，湖南 株洲412001）

随着乘客舒适性要求的提高，地铁车辆的设备气动噪声需要严格控制. 辅助变流器作为地铁车辆的重要设备，由柜体、变流器模块、变压器、风机和流道等部件组成，安装于车厢底部，四周无裙板遮挡，自身产生的气动噪声会直接辐射到车外乘客，也会以绕射、透射等方式传播到车内乘客，有必要对其进行控制.

研究人员关注地铁车辆的设备噪声. 张晓排等[1]通过测量地铁车辆在静止情况的车内噪声发现，车辆的设备噪声影响较大. 薛红艳等[2]采用噪声与振动测试分析系统对车内噪声进行测试得知，车内噪声主要为轮轨噪声和设备噪声，近车顶处噪声主要来自空调机组机械振动产生的噪声和送风口气动噪声. 任海等[3]分析了地铁车辆运行时车内噪声的成因、传播途径，并针对噪声源、隔声、减振和吸声等多方面提出控制措施. 变流器作为地铁车辆的重要设备，对车内外噪声影响的研究尚未找到，仅找到研究自身噪声大小、分布情况和简单降噪处理的文献[4-5]. 随着计算机发展和气动噪声数值仿真方法日趋完善，利用数值仿真手段预测和控制变流器气动噪声成为可能. 遗憾的是，尚未有变流器数值仿真的相关文献，只能借鉴与之相类似的文献，如空调系统等. 李启良等[6]搭建了风机、风道的气动噪声仿真模型，基于台架试验结果建立了空调系统气动噪声数值仿真方法. 风机是变流器、空调系统等设备的主要噪声源. 预测和控制风机噪声能有效解决变流器等设备的气动噪声问题. 在风机气动噪声预测方面，Lee等[7]计算了某空调用离心风机叶片通过频率噪声，首先从非定常流场中提取声源信息，然后结合边界元方法计算其噪声. Broatch等[8]采用涡分离模型对某离心压缩机的压力脉动和气动噪声进行仿真研究，考虑了风机壳体的影响，并预测到出口管道内部的啸叫声. 优化叶型和改善进入来流均匀性是降低风机噪声的主要途径. 左曙光等[9]研究了风机叶片弯角、数目、叶轮与隔板的径向间隙，明确叶轮与隔板的径向间隙对风机远场噪声的影响最大. 刘晓良等[10]研究了串列叶片不同叶片相对长度和不同叶片相对周向位置对风机气动噪声的影响. 叶学民等[11]通过数值仿真发现逆流向斜槽、双斜槽、上阶梯叶顶和下阶梯叶顶均可有效提高风机性能，叶顶形状改进后声压级随频率增大发生小幅提高，频谱形态发生明显改变. 王树立[12]通过改善离心风机进口速度均匀性实现噪声降低2.2 dB（A）.

综合以上文献调研可知，有必要建立变流器气动噪声源和传播过程的数值仿真方法，并借鉴以往噪声控制手段来实现变流器噪声的控制. 为此，本文以存在噪声超标问题的某地铁车辆辅助变流器为对象，通过数值仿真和试验相结合方法进行气动噪声研究，比较两者结果差异，寻找噪声超标原因并施加相应控制措施，为变流器开发提供参考.

1 声类比理论与气动噪声计算流程

1.1 理论基础

旋转机械类噪声主要为涡流产生的气动噪声，通常采用声类比方法进行计算. 该方法基于Lighthill法[13-14]，并结合Curle理论[15]，具体如下：

（1） Curle方程的体积分作为有限元区域的体源；

（2） Curle方程的面积分作为边界条件；

（3） 自由场的格林函数作为其它边界条件.

通过连续性方程和动量方程简化得到Lighthill声类比方程为

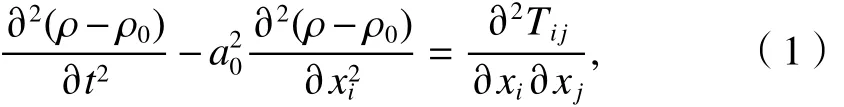
式中：t为时间；ρ为流场当地的流体密度；ρ0为流体参考密度；a0为声速；xi、xj表示不同方向的坐标；Tij为Lighthill应力.

在计算域Ω上积分，并乘以测试函数 δρ ，可得

式中：δ为迪拉克函数.

应用分部积分产生弱变分形式为

式中：ni为物体表面的单位外法向矢量在i方向上的分量；Γ为计算域的边界.

面积分上应用应力为

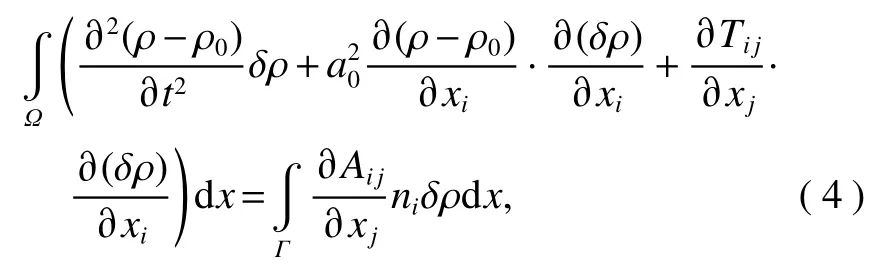
式中：总应力 Aij= ρvivj+(p-p0)δij-τij；p0为(参考压力；p为流场当地压力；粘性应力， µ 为流体动力粘度；克罗内克符号; xk为 k 方向坐标；vi、vj和 vk分别为i、j和k方向的流体速度分量.

式（4）可以表示为

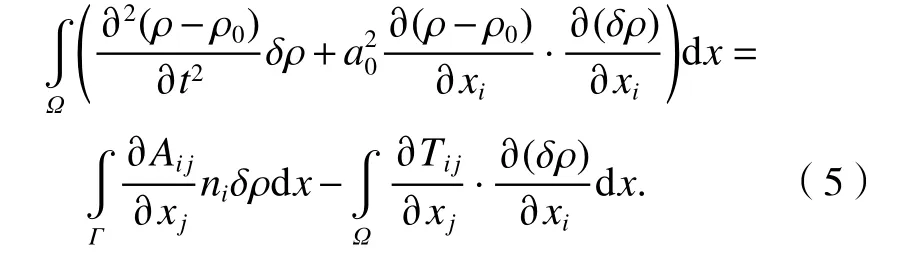
1.2 计算流程

根据式（1）～（5），辅助变流器气动噪声可采用流场和声学耦合的方法计算. 图1为辅助变流器气动噪声计算流程. 首先利用Pro/E等软件建立辅助变流器三维CAD模型；然后利用ICEM-CFD软件分别划分计算流体力学（computational fluid dynamics，CFD）网格和声学网格；再利用Fluent软件对CFD网格进行稳态和瞬态流场计算，获得辅助变流器的气动噪声源特性；接着进行ICFD （inverse CFD）转换，将速度和密度时域量快速傅立叶变换（fast Fourier transform，FFT），变换为频域结果，插值映射到声学网格上；最后进行声学计算，通过声类比法得到声源在流道和外场的声传播特性.

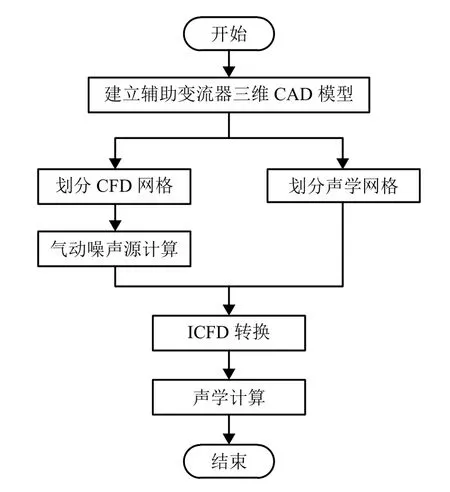
图1 辅助变流器气动噪声计算流程Fig.1 Calculation flowchart for aerodynamic noise in auxiliary converter

2 模型与仿真方法

2.1 仿真对象

图2为某地铁车辆辅助变流器结构布局和冷却风流向示意图. 辅助变流器柜体骨架由钣金件组焊而成，外部均为板结构. 离心风机安装在辅助变流器柜体内，主要由支撑部件、电机和叶轮组成，其中风机叶轮包含6个径向后弯叶片，运行过程中通过电机直接驱动. 冷却空气在风机的抽吸下由柜体顶部的2个进风口进入流道，依次冷却变流器模块、电抗器和变压器等，最后由出风口吹出. 进出风口布置有滤网，进风口和柜体中面积较大的板上粘贴了吸声材料.

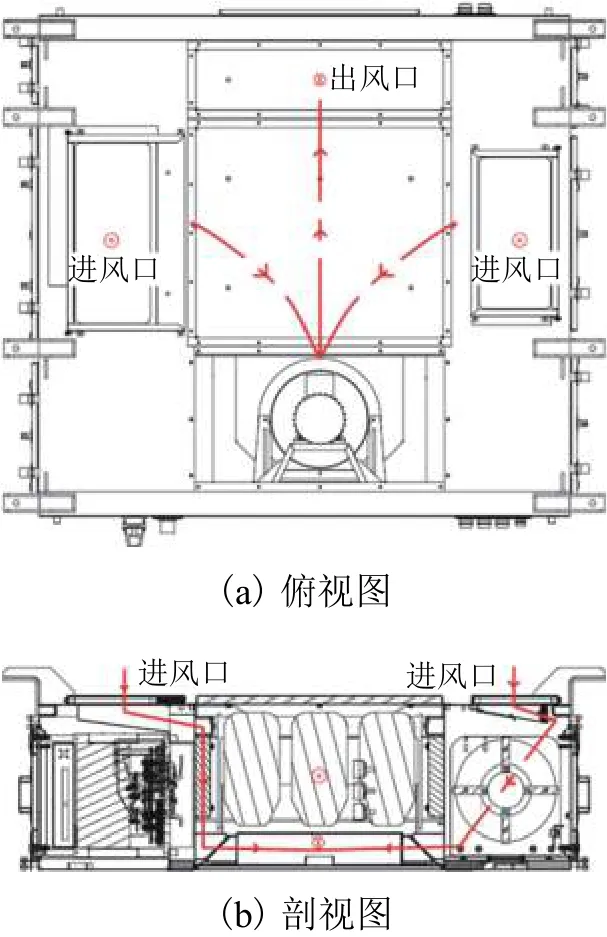
图2 结构布置和冷却风流向示意Fig.2 Schematic diagrams of structure layout and cooling air flow

2.2 网格划分

基于Pro/E软件建立的辅助变流器三维CAD模型中，各零部件包含了丰富的细节特征，比如加强筋、支座、板边、布线管、螺栓等. 这些流道的突出物虽然会对气流产生扰动，但由于流道气流速度较低（2 m/s以下），自身产生的噪声影响不大. 在本次建模中对这些突出物予以简化. 简化原则主要有：（1） 提取与空气流动和气动噪声传播相关的几何模型，如滤网、流道、风机、变流器模块散热器、电抗器、变压器和部分柜体结构等；（2） 删除对气流扰动和噪声传播影响较小的部件，如螺栓、支座等；（3） 进出风口的滤网通过设置合适阻尼参数的多孔介质材料进行等效.

辅助变流器内部流道复杂，利用ICEM-CFD软件采用四面体网格和六面体网格相结合的网格划分方法. 风机是辅助变流器气动噪声主要噪声源，需要划分精细且合理的六面体网格，在保证风机区域网格质量的同时，为了更好地满足大涡模拟（LES）要求，风机壁面首层网格质心到壁面的无量纲距离约为3. 辅助变流器流道壁面划分三角形网格，网格尺寸大多集中在3～10 mm，得到的面网格和体网格数分别为400万和1 100万. 风机区域的结构化体网格如图3所示，整个计算域的CFD网格如图4所示.

图3 风机区域的体网格Fig.3 Volume mesh of fan region

图4 辅助变流器计算域的CFD网格Fig.4 CFD mesh of computational domain for auxiliary converter

声学计算所需的网格尺寸由计算频率决定. 风机叶片数为6，转速为2 900 r/min，可知基频为290 Hz.风机在基频处会产生明显噪声峰值，且风机噪声往往呈现明显的倍频效应，因此噪声计算需覆盖5倍基频，即分析到1 500～2 000 Hz左右. 根据声学网格需要保证每波长6～8个网格的原则，计算得到声学网格尺寸不超过28.3 mm（每波长取6个网格），即可满足2 000 Hz计算要求. 基于上述原则，利用ICEM-CFD软件得到如图5所示的声学网格. 为了有效体现辅助变流器进风口和流道内部多处的吸声材料，在吸声材料所在位置定义为与吸声系数相对应的导纳边界.

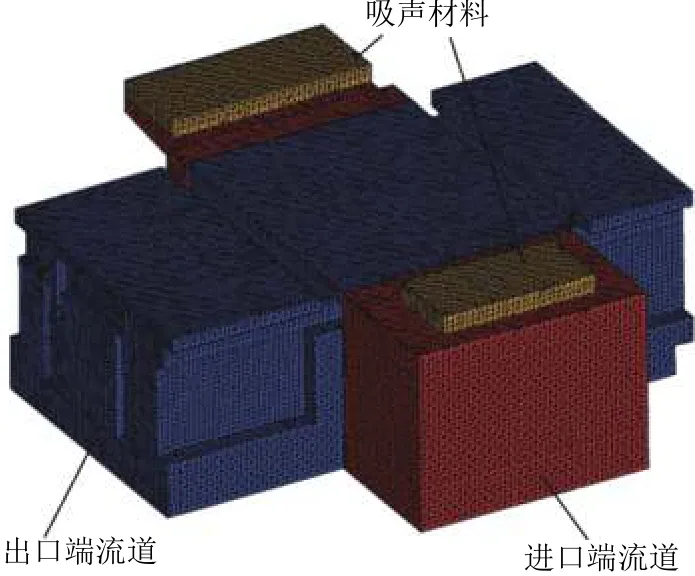
图5 辅助变流器声学网格Fig.5 Acoustic mesh of auxiliary converter

辅助变流器外部还需要参照噪声试验的条件建立声传播区域，为简化起见，设置一个包围辅助变流器柜体的立方体区域，区域的底面距离柜体底部1.05 m，设置为全反射的刚性壁面，区域的其余5个面均距离柜体表面1 m，设置为表征无反射边界的无限元边界，并针对该区域划分体网格.

2.3 仿真计算方法

采用基于有限体积法的Fluent软件进行辅助变流器气动噪声源计算时，为提高计算过程的收敛性，首先进行稳态计算，得到流场时均量，分析风机、流道内的速度、压力和流线分布特征，然后将稳态计算结果作为瞬态计算的初始场，最后进行瞬态计算. 稳态计算采用雷诺时均方程的RNG湍流模型，并结合非平衡壁面函数[16]，瞬态计算采用大涡模拟的S-L亚格子模型[17]. 考虑流体可压缩性，密度通过理想气体状态方程计算得到. 按照辅助变流器内部动静关系，将计算域分成进出风口区域和风机区域. 不同区域之间通过滑移网格交界面进行信息传递. 进出风口边界条件设置为压力边界，在固壁处采用无滑移边界条件. 压力和速度的耦合求解采用SIMPLE算法，压力项离散采用标准差分格式，动量项采用边界中心差分格式，时间采用二阶隐式格式. 仿真计算时间步长取叶片转过2° 对应的时间，即1.149 ×10-4s，其截止频率为4 350 Hz，满足风机试验结果中所关注的频率范围. 每个时间步长迭代15次，以保证每个时间步长的计算收敛. 仿真过程中，风机瞬态计算进入第3圈后，监控量呈周期性波动，因此从第4圈开始输出声源区域的密度和速度，直至第8圈才停止流场计算的迭代.

采用声学软件Actran的直接频域响应方法进行辅助变流器内外气动噪声传播计算时，将风机旋转交界面和辅助变流器内部流道区域分别定义为面声源和体声源. 为了能将流动计算所得各时间步输出的速度和密度有效输入到两类声源中，需要进行图1所示的ICFD转换步骤. ICFD转换首先进行FFT变换，将速度和密度时域量转成频域结果，然后采用积分法插值映射到声学网格中. 由于通常声学网格尺寸远小于流体网格，因而映射过程必然带来误差. 应该指出的是辅助变流器的声学网格约为所对应区域流体网格的一半，映射误差较小. 在高性能图形工作站（128 G内存，8核CPU）上，以10 Hz为频率间隔，完成一个工况的计算大约需要24 h.

3 数值仿真方法验证

辅助变流器噪声试验在凌晨于空旷的制造车间进行，将辅助变流器吊装在台架上，柜体底面距离地面1.05 m，噪声测点如图6所示. 柜体顶部两个进风口，正上方1 m分别布置1#和2#传声器；柜体四周离板中心1m 分别布置 3#、4#、5#和 6#传声器；柜体底部出风口正下方0.4 m和0.885 m各布置7#和8#传声器；柜体底部离板中心0.4 m布置9#传声器. 试验过程中发现，辅助变流器处于满载工况时，噪声较大且呈现明显的风机基频噪声.

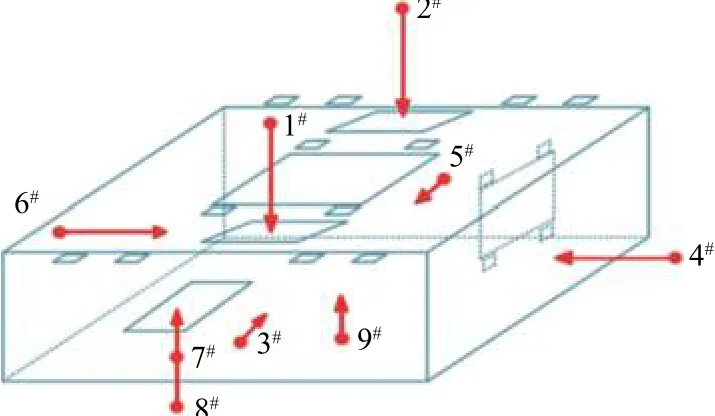
图6 噪声试验测点示意Fig.6 Measuring point location for noise test

对于旋转机械噪声问题，式（5）右边第1项为Lighthill面声源，第2项为Lighthill体声源，Actran软件的体声源与面声源设置与之对应. 分别基于面声源、体声源、面声源+体声源的设置，通过仿真计算可以得到各测点的声压级频谱. 图7为7#测点的声压级频谱. 由于噪声能量主要集中在中低频，即290 Hz附近，超过900 Hz的声压级较小，因此主要分析10～900 Hz的对比结果. 从图7可以看出，噪声曲线最大峰值频率为290 Hz，对应第1阶叶频；基于面声源的曲线与基于面声源+体声源的曲线吻合度较高，说明单独考虑面声源和同时考虑面声源与体声源差异较小，面声源对辅助变流器噪声贡献率较大，后续类似计算可只考虑面声源，而忽略体声源.

图8给出7#～9#测点仿真与试验对比曲线.从图8（a）可以看出，距出风口0.4 m的7#测点仿真结果与试验吻合度较高，290 Hz频率处峰值仅相差3 dB（A）. 仿真和试验得到的总声压级分别为79.8 dB（A）和 82.3 dB（A），相差 2.5 dB（A）. 由于辅助变流器噪声主要集中在三倍频范围内，为便于曲线的清晰对比，故在图8（b）和图8（c）的对比曲线中只展示0～900 Hz频谱曲线. 从图8（b）可以看出，距出风口0.885 m的8#测点仿真与试验得到的总声压级分别为 74.1 dB（A）和 76.8 dB（A），相差2.7 dB（A）. 从图 8（c）可以看出，距辅助变流器底部中心点0.4 m的9#测点仿真与试验得到的总声压级相差较小，但在290 Hz处有稍大差距，约为4.0 dB（A），这可能是仿真未考虑固体边界对出风口传播出来的噪声吸收或耗散作用.

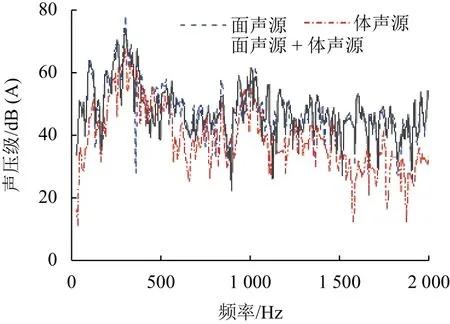
图7 7# 测点声压级频谱Fig.7 Sound pressure level spectrum of measurement point 7#

图8 不同测点声压级频谱仿真与试验对比Fig.8 Comparison between numerical simulation and test for sound pressure level spectrum at different measuring points

除290 Hz频率外，仿真与试验的声压级频谱均在70、105、250 Hz出现极大值，这可能与空腔模态有关，即发生空腔共振. 为了准确了解是否发生空腔共振，使用Actran软件进行模态计算，得到辅助变流器流道的前20阶空腔模态频率，如表1所示. 从表1可以看出，空腔的第1阶、第3阶和第9阶模态频率分别为 70.14、106.44 Hz和 247.14 Hz，与 70、105 Hz和250 Hz非常接近. 可见，这些频率出现极大值应是发生空腔共振，在后续优化中，应予以避免.

表1 前20阶空腔模态频率Tab.1 20 lowest-order mode frequencies of cavity Hz

4 噪声超标原因分析与降噪措施

4.1 噪声超标原因分析

通过噪声试验可知辅助变流器噪声超标1.5 dB（A），不满足主机厂提出的噪声指标要求，为此，可以分别从声源和声传播两方面寻找原因. 图9给出频率为290 Hz的面声源+体声源仿真得到的表征声源强度的应力张量云图. 结合图9（a）的整体分布结果和图9（b）的截面分布结果可以看到，噪声来自风机，表现为风机周期性旋转而导致明显的离散噪声. 风机区域应力张量值远大于其它区域，若风机附近隔板或壁板隔声量偏弱，会出现噪声直接穿透的情况. 进风口区域应力张量值较小，不是主要噪声源.

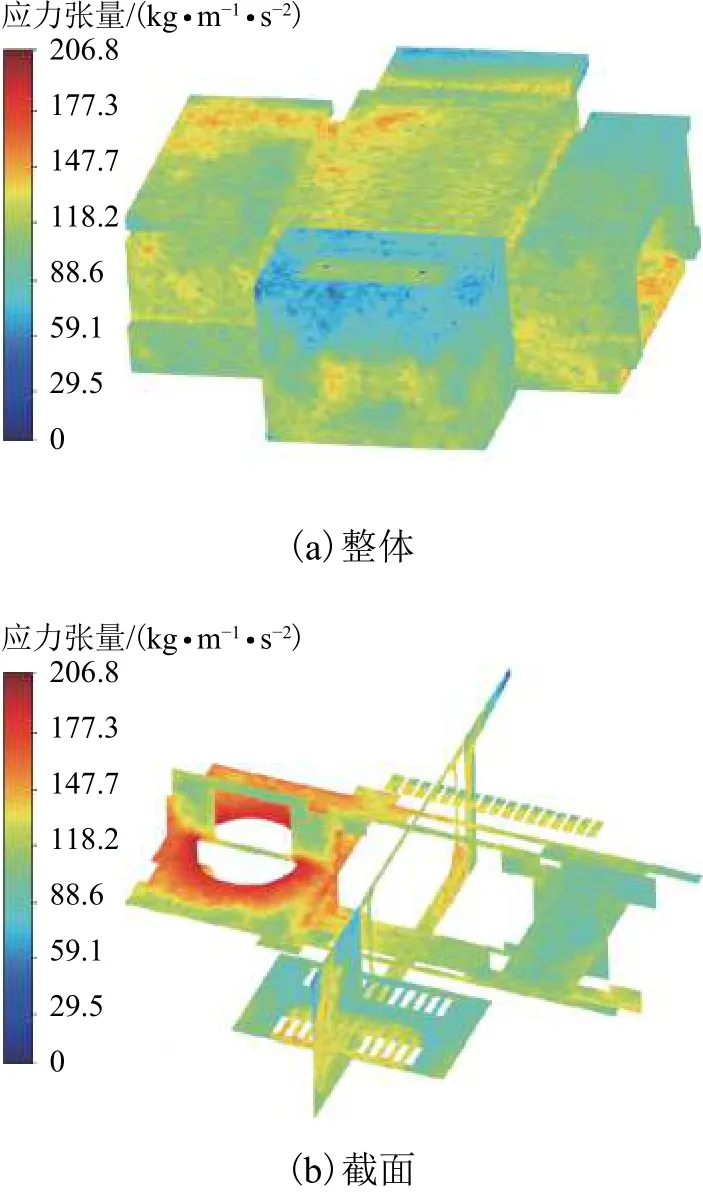
图9 气动噪声源的应力张量分布云图Fig.9 Stress tensor distribution nephogram of aerodynamic noise source

图10 给出频率为290 Hz声传播的声压级分布云图，可以看出，噪声从风机产生后，通过流道传播到辅助变流器进出风口. 由于辅助变流器两个进风口有吸声材料，内外声压级差距明显，表明该吸声材料布置和吸声效果较好. 出风口处仅有滤网无吸声材料，内部噪声直接传递出来，出风口处声压级比进风口大. 由于辅助变流器柜体壁板隔声，内部声压级比外部声压级约大35.0 dB（A）.

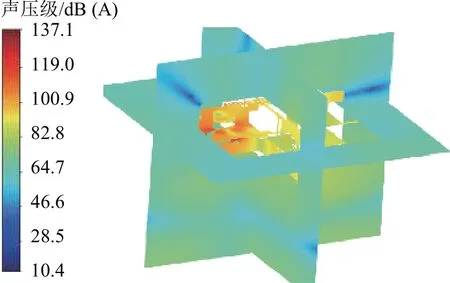
图10 声传播的声压级分布云图Fig.10 Sound pressure level distribution of sound propagation

通过以上分析可知，辅助变流器噪声超标的原因之一是风机噪声过大. 为了进一步明确风机噪声产生机理，提取0.18 s时刻风机的漩涡分布如图11所示. 从图11可以看到漩涡主要在叶片前缘产生，而且前缘靠近上轮毂面漩涡分布最广. 漩涡越过叶片前缘后逐渐开始脱离叶片表面，并慢慢向叶片压力面扩散，扩散后大涡经过叶片出口传递到辅助变流器柜体出风口区域. 风机漩涡过多且强度过大是其噪声超标的原因所在. 除风机叶片自身不合理外，还可能来自风机进口处不均匀的速度分布.

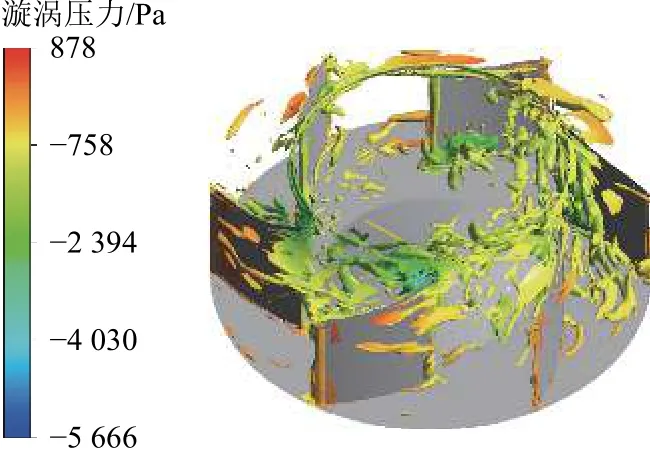
图11 风机区域漩涡分布云图Fig.11 Vortex distribution nephogram of fan region

4.2 降噪措施

为了改善风机进口速度不均匀，在风机进口端增加整流网. 整流网网孔为边长5 mm的正方形，厚度为15 mm，如图12所示. 加装整流网并经仿真计算发现，风机流量无明显改变，但速度不均匀度降低，风机进口速度均匀性得到改善.

图12 方形整流网Fig.12 Square honeycomb

图13 为有无整流网时7#测点声压级频谱对比.可以看出，增加整流网后的辅助变流器气动噪声特性仍表现为290 Hz频率处出现峰值，然而该频率峰值由原来的 74.3 dB（A）降低至 72.9 dB（A），降幅为1.4 dB（A）. 另外，在原来空腔共振频率70 Hz和250 Hz等频率处噪声均明显降低. 增加整流网后，总声压级降低2.5 dB（A），解决了辅助变流器噪声超标1.5 dB（A）的问题. 该措施应用在产品中进行噪声测试，发现各测点的噪声频谱与仿真结果的趋势基本一致，总声压级降低2.4 dB（A），降噪效果较为明显，说明降噪方案的可行性和仿真方法的准确性. 现已将增加整流网的降噪方案成功应用到产品中.

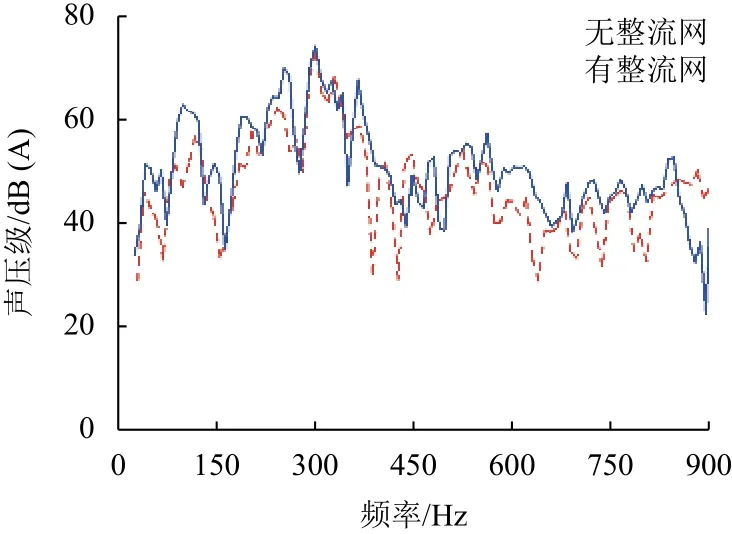
图13 有无整流网的声压级频谱对比Fig.13 Comparison of sound pressure spectrum with and without honeycomb

5 结 论

（1） 辅助变流器各测点声压级频谱的仿真与试验结果不仅趋势一致，而且量值相差较小，表明采用基于声类比方法预测辅助变流器气动噪声是正确可行的；

（2） 面声源对辅助变流器气动噪声贡献率大，而体声源贡献率小，单独计算面声源的声传播时得到噪声曲线与同时考虑面声源和体声源基本相同，后续同样类型仿真可仅采用面声源进行声传播计算；

（3） 风机进口速度不均匀是辅助变流器气动噪声超标的原因之一，通过在风机进口端增加方形整流网，相同测点总声压级降低2.5 dB（A），解决了辅助变流器噪声超标问题；

（4） 辅助变流器噪声进一步优化及其早期设计阶段气动噪声预测，均可采用本文建立的气动噪声预测方法.