四元共空间特征提取算法及其在纸币识别中的应用

盖杉

（南昌航空大学信息工程学院，江西 南昌 330063）

1 引言

随着人们对流通纸币质量要求的提高以及自动取款机和出纳机的迅速普及，银行对于自动化纸币清分技术的需求日趋强烈。纸币清分系统是一种光机电一体化的复杂产品，其主要功能是对纸币图像进行分析与处理，并根据处理结果实现对纸币图像自动分类与检测。鉴于纸币的重要性，银行对其分类的准确性要求极高。因此，纸币特征提取是纸币清分系统最为关键的环节，区分性好的特征将有利于后续识别性能的提升。

由于不同币值的人民币和意大利币几何尺寸具有差异性，Kato等[1]将纸币图像的长度、宽度等几何特征作为识别的重要依据。Takeda等[2]运用随机函数在特定区间内产生与输入特征向量维数相当的随机掩模，通过计算未被遮掩的像素个数得到特征向量，简称掩模特征方法即简记为 MASK（mask feature）方法。类haar特征[3-4]主要采用积分图像描述原始纸币图像，然后使用基于Ada-Boosting（adaptive boosting）的学习算法对原始特征向量进行选择，得到更为有效的级联分类器。刘家锋等[5]将整幅纸币图像按一定大小划分为互不重叠的矩形区域，将每个矩形区域的灰度均值作为原始特征，运用 K-L（Karhunen-Loeve）变换等方法提取更为有效的纸币图像特征，简称网格特征方法即简记为GRID方法。Choi等[6]利用离散小波变换（DWT,discrete wavelet transform）获取描述纸币图像边缘纹理信息的高频分量，将通过预先设定的阈值提取纸币图像的高频分解系数作为特征向量。盖杉等[7]采用 contourlet变换获取纸币图像不同方向与尺度上的频域信息，在此基础上引入模糊逻辑获取纸币图像识别特征（CFFE，contourlet-fuzzy feature extraction）。

上述方法虽然在纸币识别中取得了一定的效果，但是仍然存在一些不足。当纸币图像出现倾斜、折角等情况，几何特征的有效性将会下降，进而影响到最终的识别性能。掩模特征虽然能够克服纸币特征的不稳定性，但是最优掩盖集如何选取仍然是个技术难点。多尺度变换特征缺乏对纸币图像相位信息的有效描述。类haar特征计算复杂度较高，难以满足纸币实时性要求。网格特征提取的难点是如何确定方向块的大小及位置。因此如何找到一种有效的图像分析方法是提取模式有效特征、提高识别率的重要途径。四元矩阵[8-10]是一种基于频域的新图像表述方式，从解析信号组成的角度来看，四元矩阵理论是在四元代数与 Hilbert变换理论的基础上发展而来的。四元矩阵能够有效地描述图像结构纹理特征信息和局部位移信息，并且比幅值含有更多的含熵信息。

本文通过引入四元矩阵将纸币图像的结构纹理信息与相位信息作为整体直接进行分析处理，提出一种基于四元矩阵理论共空间模式纸币图像特征提取算法（QCSP, quaternion-common spatial pattern），并采用BP（back propagation）神经网络作为分类器完成识别。实验结果表明本文提出的算法能够取得较高的识别率，提取的纸币特征具有较好的可分性，并且能够满足实际纸币清分系统的实时性要求。

2 四元数统计特性

作为复数的推广，四元数是实数域基向量{1,i,j,k}的线性组合，即由一个实部和 3个虚部构成，采用式(1)定义为

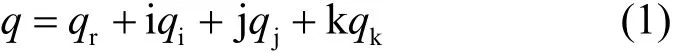
其中，qr,qi,qj和qk为实数，3个正交单位向量i、j、k 满足

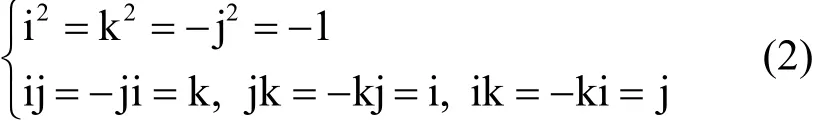
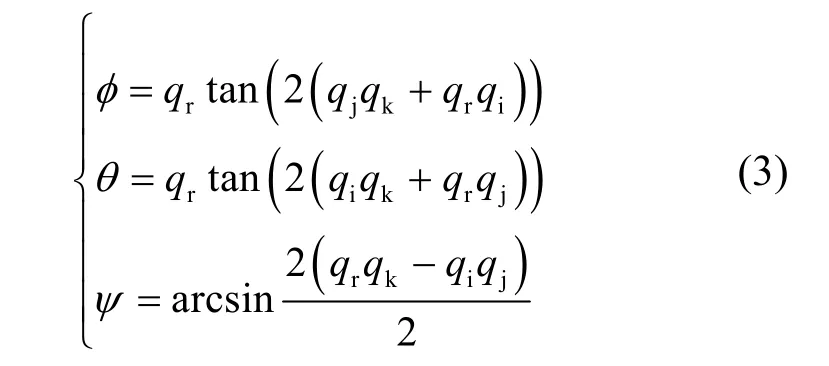
四元数乘方运算能够描述单位向量的统计信息，利用四元数具有的自反特性给出其定义，则有

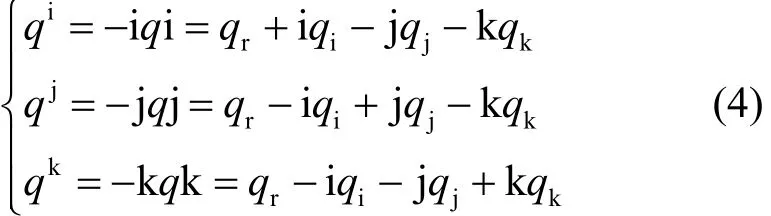
根据式(4)，给出四元向量的定义如下

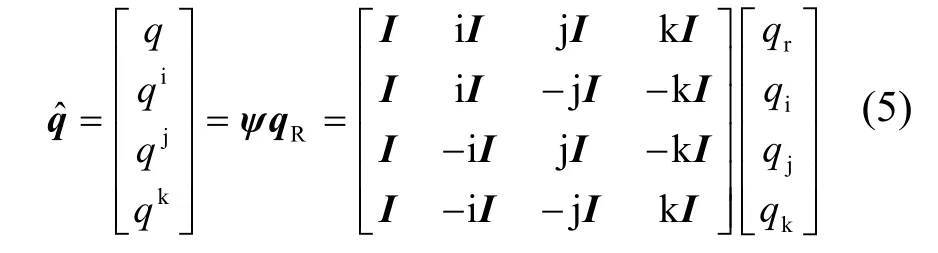
其中，I表示单位矩阵，qR表示四元数对应的实系数向量，ψ表示由实数域到四元数域的转换矩阵。令η ∈ {i,j,k}，式(4)可简化为qη=-ηq η，然后采用协方差矩阵与 3个厄米特协方差矩阵来描述四元数的实部与虚部之间具有的相关性与二阶统计特性。为了进一步解决四元矩阵的因式分解项，本文引入如下定理[11]。

定理1 设Q为四元酉矩阵，Λx为实非负对角矩阵，则对任意的四元矩阵X，其因式分解表示为

四元矩阵能够对纸币图像实现四元线性时变系统的稀疏描述，可以利用等价的复伴随矩阵对其进行快速求解。四元矩阵分解具有的3个相位信息能够描述纸币图像结构具有的互为正交方向上的强度变化。另外，四元矩阵分解具有的幅值信息能够揭示纸币图像的能量分布情况。

3 四元共空间模式特征提取

3.1 QCSP方法

受复数共空间模式构造原理启发，本文首次将复数共空间模式推广到四元数域。令xγ(γ = 1 ,2,… ,n)表示属于某类别γ的纸币样本向量，则空间协方差矩阵定义如式(6)所示。

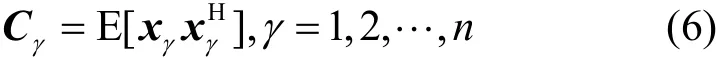
其中， E [·]表示数学期望算子。对属于类别γ的所有纸币样本空间协方差矩阵求平均值，即得到Cγ。为了能够同时对这些协方差矩阵进行对角化，给出复合协方差矩阵即，采用式(7)对该协方差矩阵进行对角化，即

其中，Cc是厄米特矩阵，U表示四元酉矩阵，Σ表示对角矩阵，H表示厄米特共轭转置算子。采用白化矩阵对复合协方差矩阵C进行白化，即

c

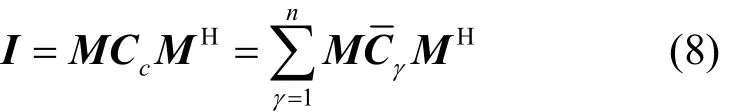
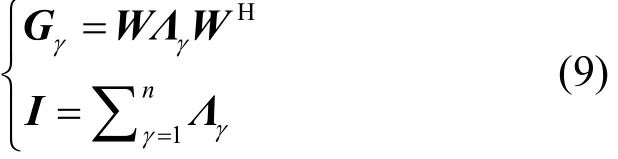
结合式(8)与式(9)，采用式(10)计算四元矩阵空间滤波器，则有

因此，纸币样本xγ经过四元矩阵空间滤波器作用后，得到矩阵yγ=Γxγ。对于四元数q=qr+qη(η = i ,j,k)，根据 STU-CCSP（strong uncorrelating transform complex common spatial pattern）算法[12]的思路，采用等价的复数描述四元数固定系数对之间的内在联系。受此启发，本文采用上述定义的厄米特协方差矩阵Cqη(η =i,j,k)来挖掘矩阵yγ分解系数之间具有的内在联系。接下来，采用式(11)对厄米特协方差矩阵Cqη(η =i,j,k)进行扩展，则有

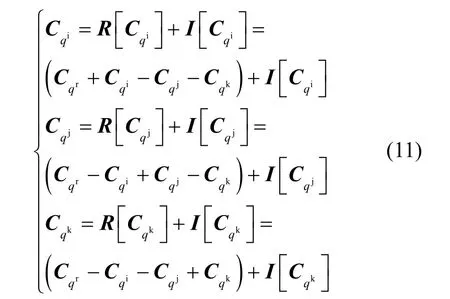
其中，厄米特协方差矩阵可以分解为如式(2)所示。

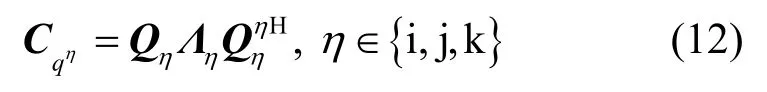
其中，Qη为四元酉矩阵，Λη为实对角矩阵。结合式(11)与式(12),Λη定义为

如上所述，对于纸币样本xγ，经过四元滤波器作用后得到四元分解矩阵yγ，采用四元数实部与虚部的方差作为纸币图像分类识别的特征向量，即

采用式(14)～式(17)计算得到属于某一类别的纸币样本特征向量

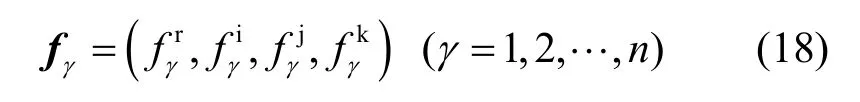
综上所述，基于四元共空间模式特征提取算法的具体步骤如下：

步骤1定义所有类别的空间协方差矩阵Cγ；

步骤2计算复合协方差矩阵Cc，并对Cc进行对角化；

步骤3计算白化矩阵M与白化数据vγ=Mxγ，并对Cc进行白化操作；

步骤4对矩阵Gγ进行对角化，并计算得到特征向量W；

步骤 5计算厄米特协方差矩阵

步骤 6构造复合厄米特协方差矩阵Ccη=并对Ccη进行对角化

步骤 7计算标准四元矩阵滤波器和复合四元矩阵滤波器

步骤8根据yγ=Γcx与yηγ=Γηx，计算纸币样本的特征向量

3.2 QCSP算法理论分析

本文提出的QCSP特征提取算法不仅具有较高的稳定性，同时还具有较低的时间计算复杂度。首先，从数学分析的角度证明本文特征提取算法的稳定性。对于在高速采集过程中受噪声干扰的纸币样本向量定义如式(19)所示。其中，xγ′是原始纸币样本，Τψ是四元矩阵变换，μ是纸币特征区域上的噪声信号。通过引入条件理论中的变换条件数作为特征稳定性的度量，基于变换集合Θ，给出类条件数定义，则有

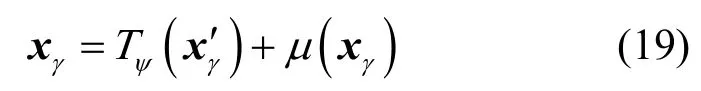
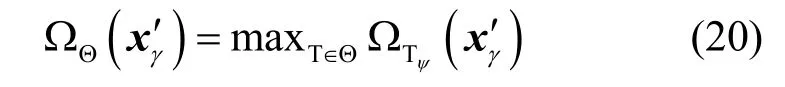
式(20)存在下界，即

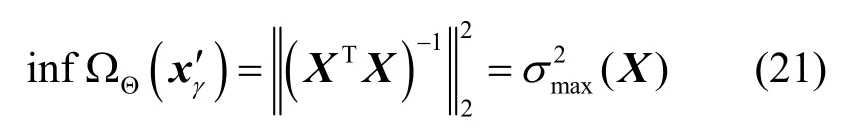
其中，X表示四元矩阵， σmax(X)是四元矩阵的最大奇异值。因此，当XTX的奇异值足够大时，QCSP算法能够获得足够稳定的特征向量。另外，采用式(5)计算得到四元向量的增广向量qˆ =ψqR，其具有的增广协方差矩阵定义为

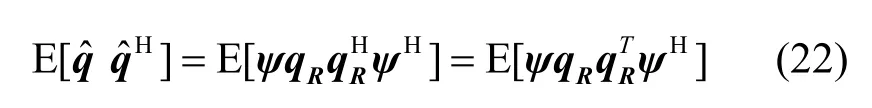
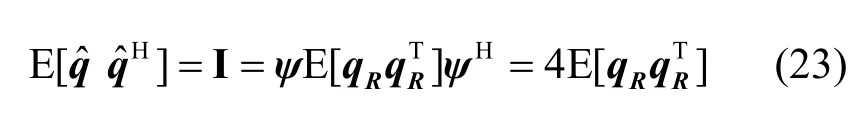
经上述推导，并结合式(22)与式(23)，可以得出QCSP特征提取算法的时间复杂度是基于复数共空间模式特征提取算法的四分之一。因此，基于QCSP纸币特征提取算法能够满足实际纸币清分系统对实时性的要求。

4 实验结果与分析

4.1 实验数据库构建

本文自行设计清分系统的图像模块采用基于“接触式传感器(CIS)-FPGA-DSP”的结构模式。将对实时性要求较高的逻辑运算放在FPGA中完成，将纸币图像预处理、特征提取与识别放在DSP中完成。为了验证本文提出算法的有效性，从自行设计的纸币清分系统中分别采集人民币、美元与欧元构建3个纸币图像数据库。

纸币图像样本是通过接触式图像传感器得到，具体构建的3个实验数据库描述如下：1) 数据库1(D1, database 1)由20 000张人民币样本图像组成，具有100元、50元、20元、10元、5元等5个主币，每个币值有4个面向，共有20种图像；2) 数据库2 (D2, database 2)由18 000张美元样本图像组成，具有100美元、50美元、20美元、10美元、2美元、1美元6种主币，每个币值有4个面向，共有24种图像；3) 数据库3 (D3, database 3)由15 000张欧元样本图像组成，具有500欧元、200欧元、100欧元、50欧元、20欧元、10欧元、5欧元7种主币，每个币值有4个面向，共有28种图像。其中，全新的纸币样本有32 860张，占比62%；各种污损纸币样本为15 105张，占比28.5%；扭曲变形和噪声纸币样本为5 035张，占比9.5%。

4.2 纸币图像预处理

本文中所处理的纸币图像样本来自于高速扫描装置，纸币在一个机械通道中高速运行，由图像传感器对其进行扫描，获得图像信息。由于纸币在通道中高速连续运行，这样就不可避免地造成纸币图像发生倾斜、侧移等现象。因此在进行纸币图像特征提取之前需要经过一个预处理过程，首先利用钱币图像边缘为直线的特点，采用在图像上等间隔位置检测边缘的方法，在每一条边上检测出一个边缘点序列，然后对边缘点序列采用最小二乘拟合得到钱币图像的边缘。

4.3 QCSP算法实验结果

为了验证本文提出算法的有效性，将QCSP算法应用于纸币识别中，并将QCSP算法与一些经典的纸币特征提取算法如DWT[6]算法、MASK[2]算法、GRID[5]算法和 CFFE[7]算法进行比较。另外，鉴于BP神经网络能够自适应地发现纸币样本数据之间的规律性，而且具有较强的自学与自组织能力，本文将BP神经网络作为纸币识别阶段的分类器。使用BP神经网络结构的输入层节点个数为提取纸币图像的特征维数，输出层节点个数为各币种具有的面值与面向，2个隐含层节点个数分别为18与32，训练权系数更新步长为0.1，最小误差为10-8，最大迭代次数为9×104次。数据库D1～D3中测试样本的平均识别率如图3～图5所示，实验结果表明采用本文提出的QCSP算法所获得的平识别率明显高于其他 4种算法，3个数据库的识别率分别提高到98.86%, 99.18%与93.68%。

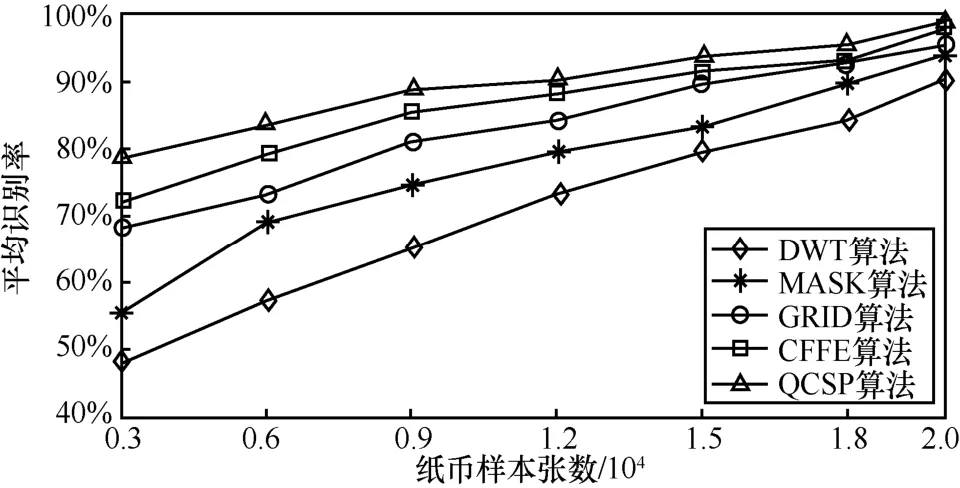
图1 人民币数据库D1平均识别率

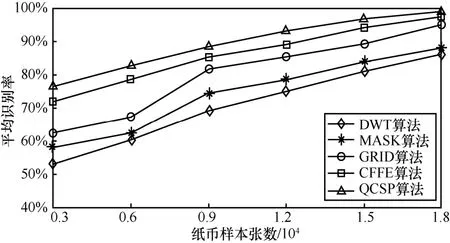
图2 美元数据库D2平均识别率

为了进一步验证本文提取纸币特征的抗干扰性，对其中15 105张具有不同污损程度的纸币样本进行实验。采用 DWT算法、MASK算法、GRID算法、CFFE算法和QCSP算法的纸币识别率分别为82.31%，88.54%，92.57%，96.89%和98.24%，这本文提出的QCSP算法纸币特征提取算法相比于其他算法能够更有效地克服污损对纸币图像特征造成的影响。另外，在采集大量纸币样本的过程中，不可避免地会出现样本图像残缺不全、受噪声干扰导致纸币图像定位不准确以及纸币图像倾斜过大等情况，针对上述情况，本文在纸币识别阶段引入拒识类的策略，有效地增加了算法的稳定性。表1～表3显示了采用本文提出的QCSP算法与DWT算法、MASK算法、GRID算法、CFFE算法所得到的实测识别率与拒识率。实验结果表明采用本文提出的QCSP算法较其他4种方法取得了更高的识别率和较低的拒识率。

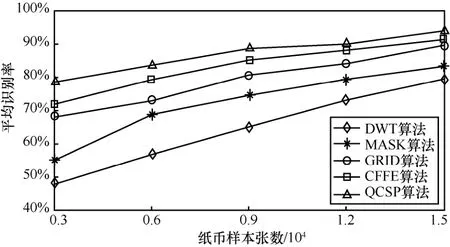
图3 欧元数据库D3平均识别率

在Intel Core I7 2.4 GHz CPU和8 GB RAM的平台上给出纸币特征提取与识别的运行时间如表 4所示。实验结果表明本文算法较其他算法具有更低的时间复杂度。另外，纸币清分系统是一种高速运行的装置，考虑到纸币图像扫描装置与控制装置的动作时间，本文提出的算法较其他算法更能够满足纸币清分系统的实时性要求。

5 结束语

针对纸币图像具有丰富的相位结构特征信息，结合四元矩阵自身的特性，本文提出一种基于四元共空间模式的纸币图像特征提取算法。该算法能够有效地克服掩模特征的不稳定性以及网格特征较难区分风格相近纸币图像的难题。另外，本文提出的算法还能够弥补小波变换与 contourlet变换缺乏对纸币图像相位信息描述的缺陷。为了验证提出算法的有效性，本文将其应用到纸币识别系统中，实验结果表明本文提出的算法不仅能够取得较高的识别率，而且对于污损、扭曲变形和受噪声干扰的纸币图像也具有良好的可分性。为了进一步提高纸币识别的稳定性和准确性，本文在纸币识别阶段引入拒识类的策略。本文提出的算法已成功应用在一个资源约束的嵌入式清分系统中，并且能够满足系统实时性的要求。

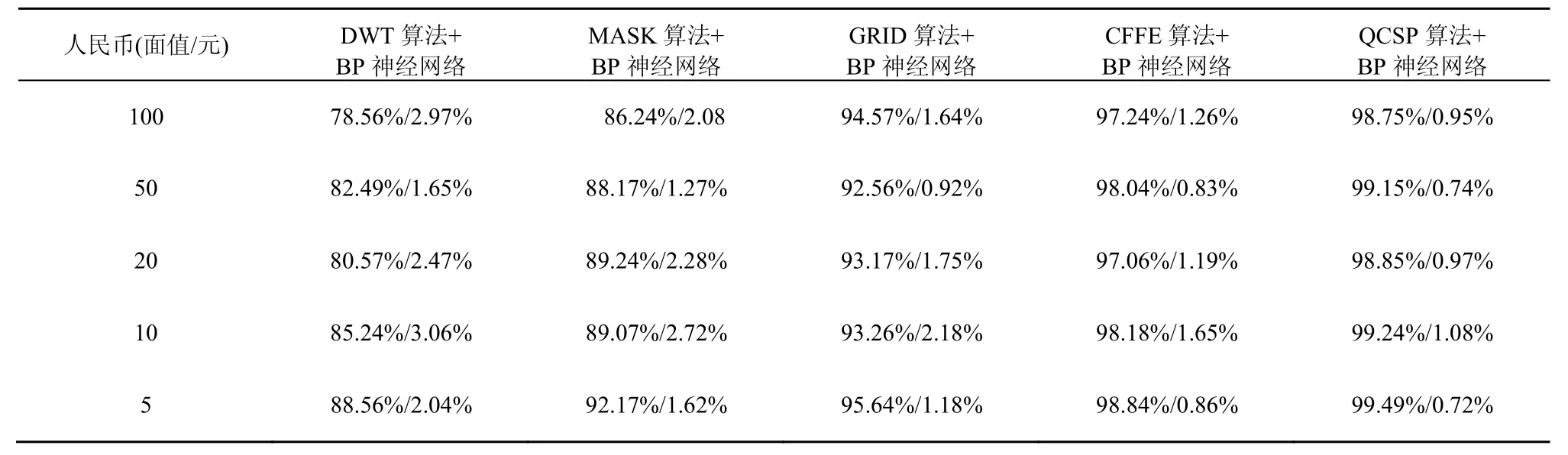
表1 数据库D1实际测试数据（识别率/拒识率）

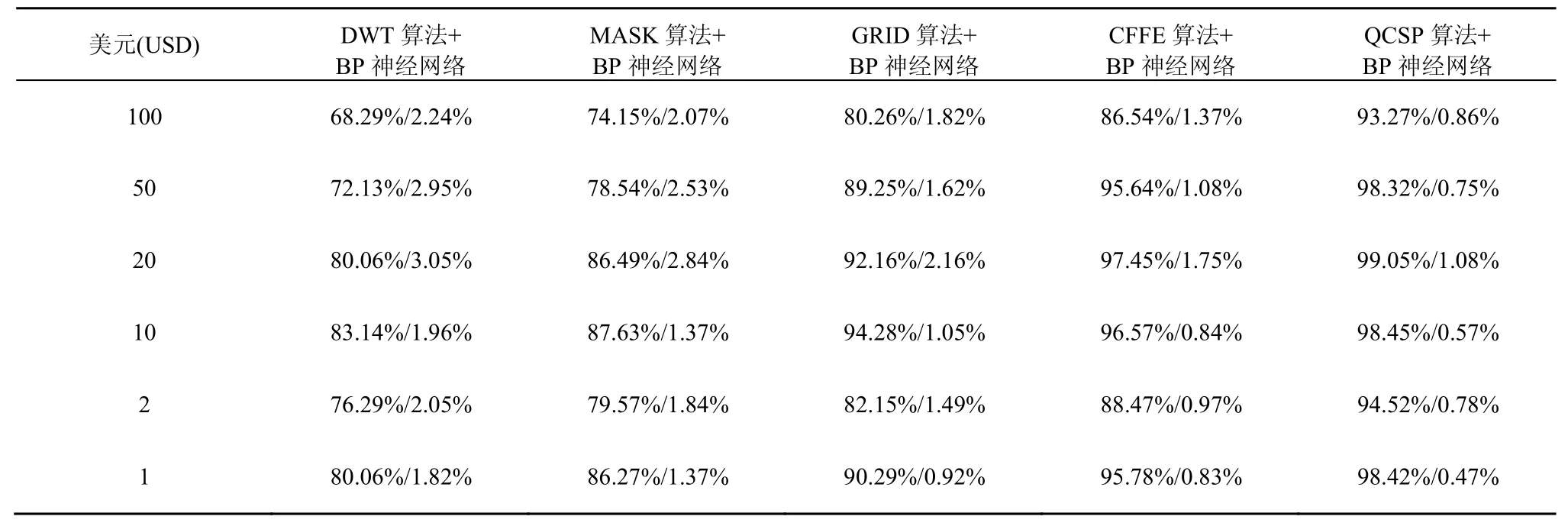
表2 数据库D2实际测试数据（识别率/拒识率）

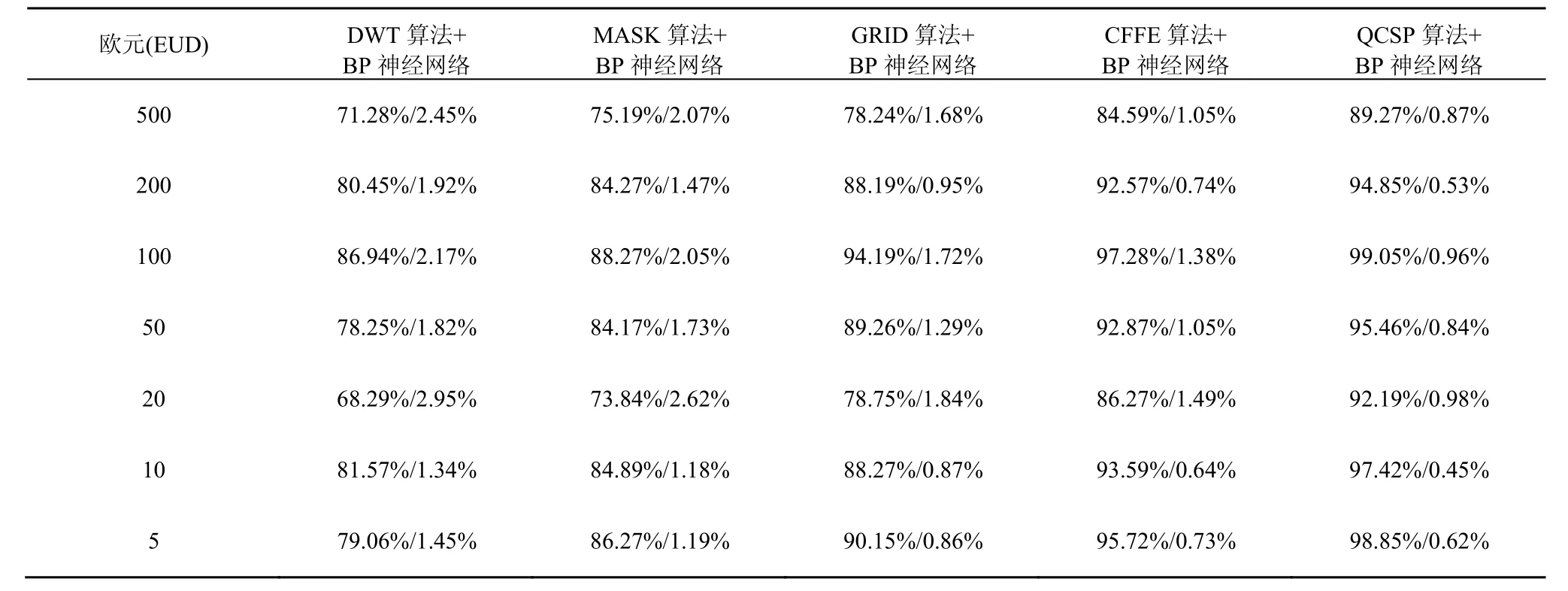
表3 数据库D3实际测试数据（识别率/拒识率）

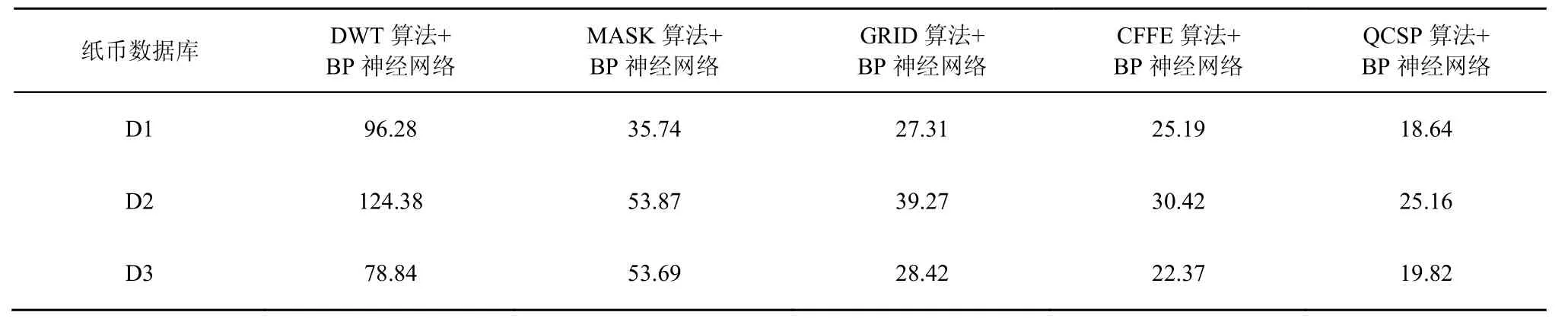
表4 纸币识别时间/ms