基于MMG标准的船舶四自由度操纵运动仿真

黄蓉蓉，李 星

(江苏润扬船业有限公司，江苏 扬州 225217)

0 引言

船舶操纵性对于船舶航行安全至关重要。为设计优良的操纵运动控制系统，需要对船舶进行操纵运动仿真，获得其操纵运动性能。日本JTTC的MMG小组于1977年[1]提出了MMG(Maneuvering Modeling Group)操纵运动方程，并针对MMG方法使用的数学模型及水动力系数进行了诸多研究[2-4]。传统的MMG方程使用纵荡—横荡—艏摇三自由度运动方程，而针对高速舰船以及初稳性高GM值较小的船舶如集装箱船，其操纵运动对横摇方程的影响不容忽视，需要考虑纵荡—横荡—艏摇—橫摇四自由度运动方程。同时为使得MMG方程变得更为通用，需要对MMG方程进行标准化研究[5]，并对MMG方程的细节进行标准化。

目前国内针对四自由度MMG方程也开展了较多研究[6-8]，但主要研究传统四自由度MMG方程。本文基于MMG标准方程，进一步构建了纵荡—横荡—横摇—艏摇四自由度运动方程，详细介绍了MMG分离型船桨舵数学表达，并以某集装箱船为对象，开展不同舵角下操纵性数值仿真试验，验证该方法在实际尺度下进行操纵性预报的可行性。

1 MMG标准操纵性数值仿真模型

1.1 基本假定及坐标系

船舶操纵性数学模型基本假定如下：

(1)船体为刚性体。

(2)作用在船体上的水动力是准定常的。

(3)船体横向速度分量相比纵向速度为小量。

(4)不计船舶兴波影响。

(5)横摇耦合影响忽略不计。

MMG数学模型采用的坐标系如图1所示。考虑到船舶操纵回转呈水平面运动，本文对z方向不作研究。图中：o0-x0y0z0固接于地球的固定坐标系，采用右手直角坐标系；o0x0轴为固定坐标系纵轴，沿水平面内指向初始航向；o0y0轴为固定坐标系横轴，向右为正；o0z0轴为固定坐标系垂直轴，向下为正。

运动坐标系o-xyz同样采用右手坐标系。坐标原点o位于船舯；ox指向船艏为正；oy轴指向右舷为正；oz轴垂直于水平面向下为正；u和vm分别为x和y方向的速度分量；r为偏航角速度；首向角Ψ定义为o0x0与ox的夹角；U为航速；δ为舵角；重心G位于o-xyz坐标系的(XG，0，0)处。

图1 MMG数学模型采用的坐标系

1.2 运动方程

本文在MMG方程的基础上，增加横摇运动方程，并考虑重心处横向速度v=vm+xGr，可以获得重心处船体水动力和力矩具体表达式，见式(1)：

(1)

同时，作用于船体的X、Y、N和K可以表达为流体惯性力项和流体粘性力两部分。式(1)右边项表达见式(2)：

(2)

1.3 船体的水动力和力矩表达

式(2)中船体水动力XH、YH和力矩项NH、KH表达见式(3)：

(3)

式中:ρ为水密度;LPP为垂线间长;d为船舶吃水；上标一撇表示无量纲值。

XH、YH、NH、KH无因次展开见式(4)：

(4)

1.4 螺旋桨及舵力水动力表达

纵向螺旋桨推力XP表达式见式(5)：

XP=(1-tp)T

(5)

式中：tp为推力减额；T为螺旋桨推力，其具体表达式见式(6)：

(6)

式中：np为螺旋桨转速；Dp为螺旋桨直径；KT为敞水桨推力系数;JP为螺旋桨进速系数。

有效舵力XR、YR、NR的表达式见式(7):

(7)

式中：tR、aH、xH为船体与舵之间水动力干扰系数；FN为舵法向力,其具体表达式见式(8)：

(8)

式中：AR为舵面积；fα为舵法向力系数，一般采用藤井公式进行估算；UR和αR分别为计入船体、螺旋桨影响后舵前的有效流速和有效舵角。

2 船舶操纵运动数值仿真

根据式(2)和式(3)所示的MMG操纵运动方程，利用Matlab对基于MMG标准方法的船舶四自由度运动方程进行建模， 并针对某集装箱船开展回转操纵运动仿真。集装箱主尺度见表1，集装箱船无因次位置导数、旋转导数及耦合导数值见表2。

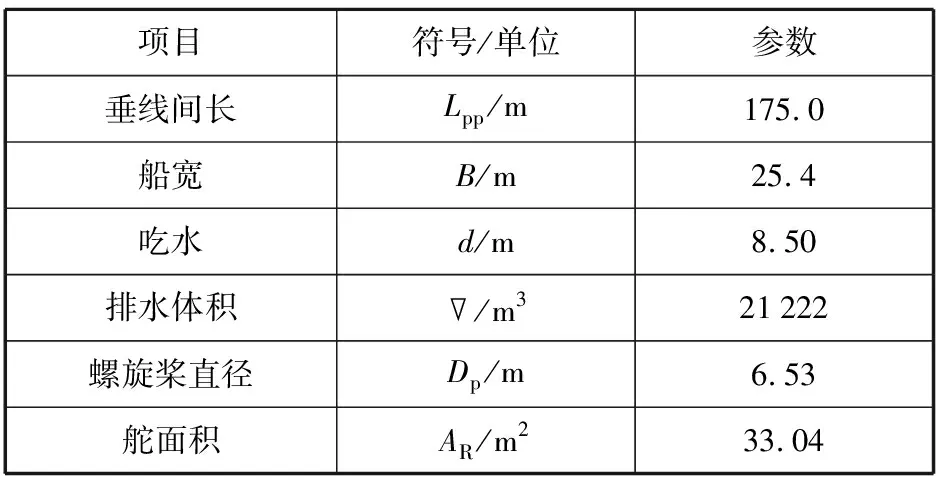
表1 集装箱船主尺度

表2 集装箱船水动力系数

针对四自由度操纵运动方程，采用四阶龙格库塔算法进行求解。计算中，仿真过程时间步长设置为0.01 s,航速为15.5 kn，相对误差设置为1×10-5，初始状态时v、p、r、Φ、Ψ、x以及y均为0。图2给出了集装箱船在15.5 kn航速时，采用MMG四自由度运动方程模拟船舶回转运动时，左旋35°、30°、25°、20°以及右旋35°、30°、25°、20°回转理论计算曲线，其中坐标轴分别为x、y的无因次表达。表3给出了回转运动中纵距AD、横距AT、定常回转直径D以及战术直径DT的无因次计算结果。由图中轨迹线可以看出舵角±35°时回转直径最小，±20°时回转直径最大。图3给出了左旋35°～20°时回转运动过程中速度及角速度变化曲线。由图可以看出，35°时回转角速度最大，速降也最大，故而其定常回转直径最小。

图2 集装箱船不同舵角回转理论计算曲线

舵角δ纵距AD/LPP横距AT/LPP定长回转直径D/LPP战术直径DT/LPP35°3.264.123.423.9930°3.374.423.904.3725°3.685.024.544.8620°4.045.675.285.50

3 结语

针对高速船及GM值较小的集装箱船等船型操纵运动时的横摇耦合影响问题，在标准MMG纵荡—横荡—艏摇三自由度运动方程的基础上，本文首先详细介绍了考虑横摇耦合影响的纵荡—横荡—艏摇—横摇四自由度数学模型，包括船体水动力系数表达、舵力以及螺旋桨推力的标准公式；其次基于MMG标准方法对某集装箱船建立全尺度下的仿真数学模型，在Matlab平台下编写程序进行不同舵角下的回转仿真试验。试验结果表明：船舶操纵运动的仿真研究，可以为实际船舶操纵性快速预报提供参考。

图3 速度变化曲线