水下航行器三维航迹反演滑模跟踪控制

孙巧梅，陈金国，余 万

(1. 三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002；2. 中国船舶重工集团有限公司第七一〇研究所，湖北 宜昌 443003)

0 引 言

自治水下机器人系统是一种典型的非线性强耦合系统。由于AUV工作环境复杂、水动力参数难以精确求解等原因，AUV非线性系统的运动控制问题成为控制领域的研究热点。张利军等[1]针对垂直面欠驱动自治水下机器人定深控制问题，仅使用可测量的深度和纵摇角信息，基于反演法设计自适应输出反馈控制器。 俞建成等[2]提出了基于广义动态模糊神经网络的水下机器人直接自适应控制方法，通过在线自适应学习算法构建水下机器人的逆动力学模型。提出了基于网络结构的水下航行器直接自适应控制器，利用Lyapunov稳定理论，证明了基于该控制器的水下航行器控制系统闭环稳定性。Lee等[3]为提高鲁棒性、解决系统耦合项纵向速度对航向的影响，设计了性能较好的AUV深度L1自适应控制器。

AUV轨迹跟踪控制的目标是设计有效的控制律，使其从初始状态跟踪参考轨迹，并保证跟踪位置误差的全局一致渐进稳定[4-5]。目前研究成果采用的控制方法主要有传统PID控制方法、滑模控制方法、反演控制方法、神经网络法。由于传统PID参数需要适应模型参数的变化，而AUV动力学模型参数存在不确定性，因此很难满足需要。胡志强等[6]提出了USV系统航向在线自优化 PID（比例、积分、微分）控制算法。

变结构滑模控制凭借其强鲁棒性，在AUV的轨迹跟踪控制中取得了一些成果[7-8]。魏延辉等[9]提出一种基于解耦模型的多控制器联合控制方法。对解耦后的AUV运动模型进行轨迹跟踪控制器的设计，为轴向和侧向运动设计自适应反演滑模控制器，为首向运动设计带有干扰观测器的自适应终端滑模控制器。Conte等[10]采用滑模控制律提出一种小型水面船跟踪水下目标的轨迹跟踪控制系统，取得了满意的效果。Zool H. Ismail等[11]提出了一种基于鲁棒动态区域的滑模控制并应用于水下航行器的轨迹跟踪，并与模糊滑模和自适应模糊控制进行比较，取得了满意的效果。Gao等[12]将AUV六自由度运动模型解耦成垂直和水平面2部分，并且分别设计了有效的滑模控制器。Hnagil J等[13]针对存在未知干扰的AUV三维运动，采用二阶滑模控制器，通过实验证明控制器能够提高轨迹跟踪的精度。贾鹤鸣等[14]提出了基于神经网络的自适应输出反馈控制方法来研究水下机器人三维轨迹跟踪，控制器由基于动态补偿器的输出反馈控制项、神经网络自适应控制项和鲁棒控制项。 Liu等[15]提出了一种基于模糊神经网络的鲁棒自适应控制策略，用模糊神经网络是用来估计反演控制律。反演控制策略是AUV常用的控制方法。Lionel L等[16]提出的基于反步控制与Lypaunov函数的AUV非线性路径跟踪控制方法，Jon E R等[17]将反步控制与模型反馈控制结合应用于欠驱动水下机器人控制之中。

本文针对三维水下航行环境中AUV航迹精确跟踪问题，提出了自适应反演滑模跟踪控制器。基于Lyapunov稳定理论分析了整个闭环系统的稳定性。在Matlab软件上通过对光滑的指令航线进行跟踪仿真，结果表明所设计的控制器可以很好地克服时外界干扰，取得较好的航迹跟踪效果。

1 AUV数学模型

通常用六自由度数学模型来描述AUV的复杂运动，假设其具有截面、切面和断面3个严格对称的对称面，且假设重力和浮力相等。2个参考坐标系为惯性坐标系和载体坐标系。根据牛顿欧拉公式，AUV的运动学和动力学方程为：

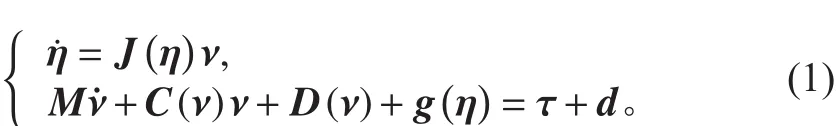
为了简化轨迹跟踪[控制器的]设计，这里将横滚自由度忽略掉，式中 η =x,y,z,θ,ψT是AUV位置和姿态向量[，描述其]在惯性坐标系中水平位置及艏向角，ν=u,v,w,q,rT为AUV的5个自由度的线速度和角速度。M为(包)含附加质量的惯量矩阵且 M=MT＞0，M˙=0。 Jη 为坐标变换矩阵， C(ν)ν为包含了质量矩阵和附加质量矩阵引起的科氏力与向心力且C(ν)=-CT(ν)， D(ν)为黏性水动力系数矩阵且D(ν)＞ 0，g为恢复力和力矩，为各自由度的力和力矩，d为外界干扰。

由式（1）可以得到

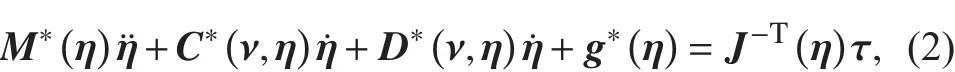
式中：

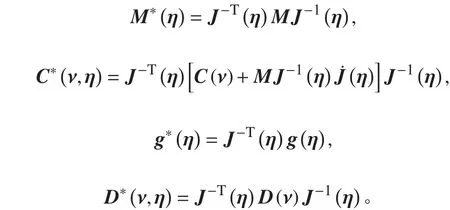
2 轨迹跟踪控制器设计

控制目标为设计一个自适应鲁棒控制器使AUV状态向量跟踪预定三维航迹，跟踪误差趋近于0。

1）反演控制律

航迹跟踪[控制的目]的是设计控制律满足式AUV系统状态η =x,y,z,θ,ψT趋近于ηr，跟踪误差为e1=η-ηr，那么有e1=-r。

定义第1个Lyapunov函数为

所以有

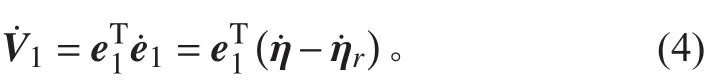
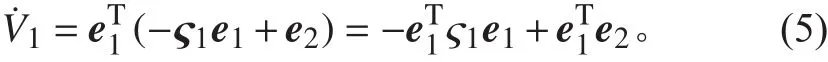
由AUV系统方程得

2）滑模项的推导

由于传统的反演控制方法无法克服扰动，这里通过引入滑模项，保证控制系统的鲁棒性。

设滑动面s=e2，定义第2个Lyapunov函数为

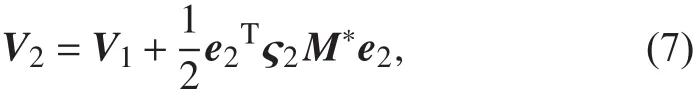
式中 ς2∈ R5×5是正定对角阵，则

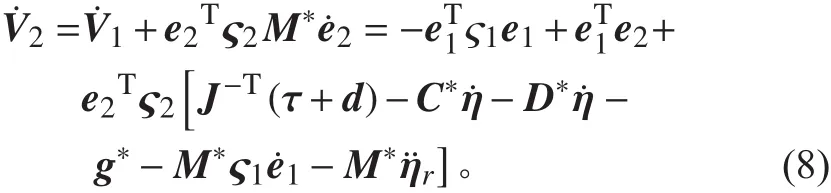
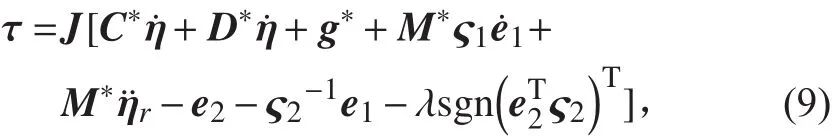
式中d为外界干扰，在实际中通常是有界的。如果保证λ ≥ |J-Td|，则≤0，所以 e1和 e2收敛，且当时，有e1→0和 e2→0，所以控制系统能够达到稳定。由于e1=η-ηr，e2=，则，

3 仿真验证

采用本文控制设计的方法，在Matlab环境下通过控制AUV在不同参考航迹下进行轨迹跟踪，同时也对PID控制器作用下的AUV轨迹跟踪进行对比，从而验证本文提出的滑模反演法的有效性。

AUV主要参数如表1所示。

表1 AUV主要参数Tab. 1 AUV main parameters

同时假设AUV受到的环境干扰为

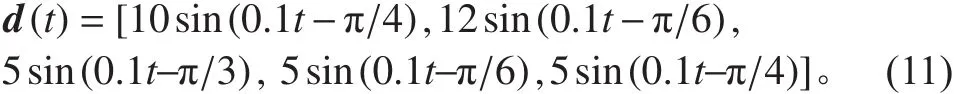
1）给定期望航迹为一光滑三维航迹：

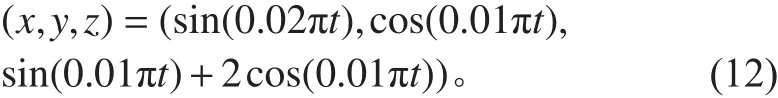
仿真结果如图1～图4所示。

图1和图2分别给出了在设计的控制器和传统PID控制器作用下单独每个坐标轴上的跟踪曲线，图3和图4为在设计的控制器作用下的仿真结果，图3为AUV三维空间航迹跟踪曲线，图4为每个坐标轴的上跟踪误差。从图中可以看出，反演滑模控制器控制的AUV能很好地跟踪上期望轨迹，而且分别在x，y，z轴上跟踪误差小。和传统PID控制器相比，能更好的克服外界干扰，避免初始时的过调，具有较强的鲁棒性，从而使AUV快速准确的实现轨迹跟踪。

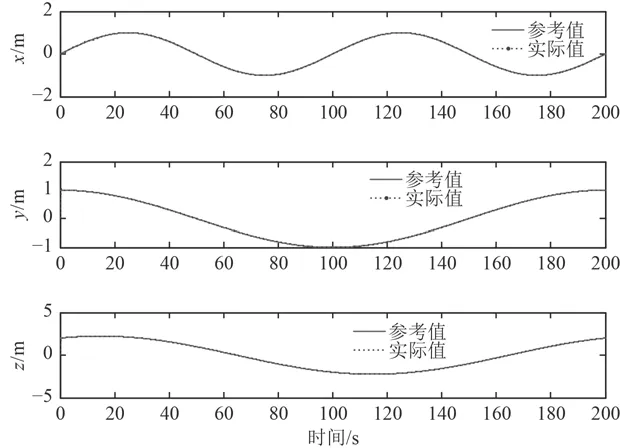
图1 反演滑模控制AUV的xyz轴航迹跟踪曲线Fig. 1 AUV trajectory tracking based on backstepping SMC

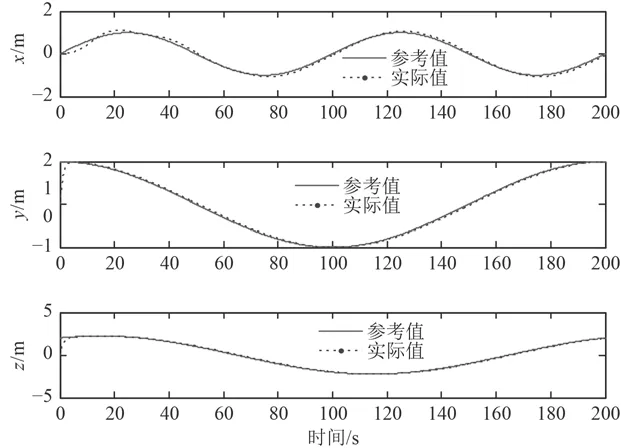
图2 PID控制AUV的xyz轴航迹跟踪曲线Fig. 2 AUV trajectory tracking based on PID

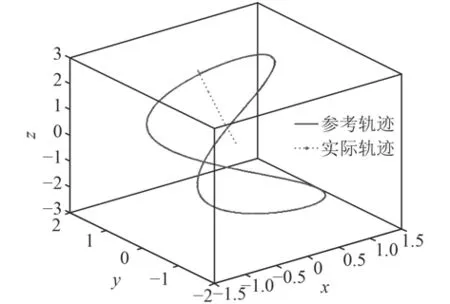
图3 AUV空间航迹跟踪曲线Fig. 3 AUV main parameters

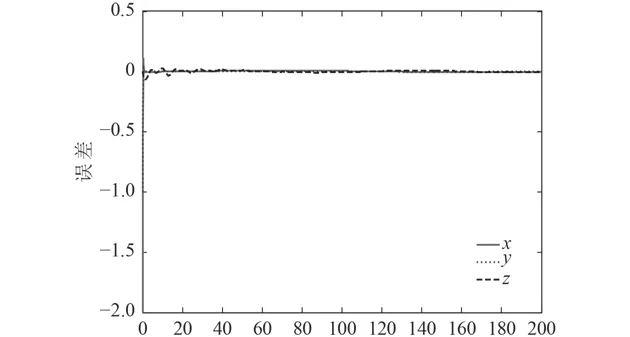
图4 xyz轴航迹跟踪误差曲线Fig. 4 AUV 3D Trajectory

2）设定AUV航迹制导器生成的期望航迹点为

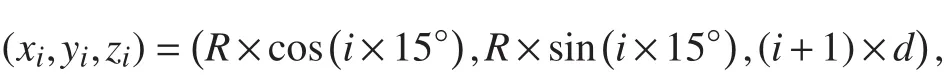
其中R=10，d=2，由期望航迹点拟合产生三维航迹进行跟踪控制。

在螺旋线为期望轨迹的前提下，图5和图6分别为在本文设计的控制器和传统PID控制器作用下单独每个坐标轴上的跟踪曲线，图7和图8为在设计的控制器作用下的仿真结果。从仿真结果可以看出，反演滑模控制器控制的AUV能很好地跟踪上期望轨迹且分别在x，y，z轴上跟踪误差小。和图6所示传统PID控制器结果相比，能更好地克服外界干扰，避免初始时的不稳定，具有较强的鲁棒性，从而使AUV快速准确的实现轨迹跟踪。

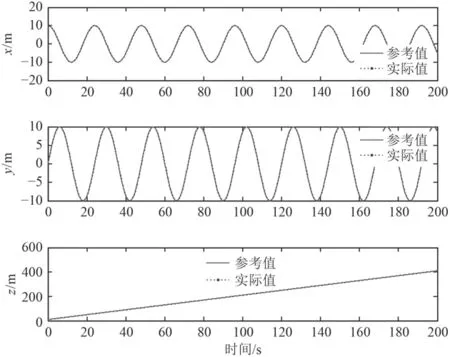
图5 反演滑模控制AUV的xyz轴航迹跟踪曲线Fig. 5 AUV trajectory tracking based on backstepping SMC

图6 PID控制AUV的xyz轴航迹跟踪曲线Fig. 6 AUV trajectory tracking based on PID

图7 AUV空间航迹跟踪曲线Fig. 7 AUV 3D helix trajectory

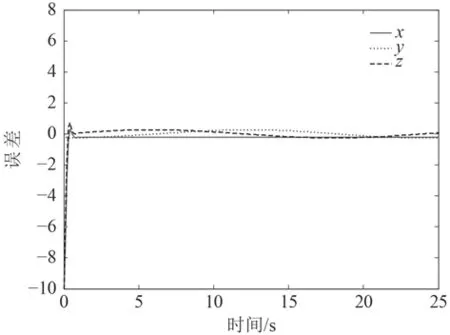
图8 xyz轴航迹误差曲线Fig. 8 Tracking control error

4 结 语

本文针对自治水下航行器的三维轨迹跟踪问题，利用反演滑模算法构造了轨迹跟踪控制器，在给定的光滑航迹下进行控制系统的仿真验证，并且与PID控制器的作用效果进行对比。由结果可以看出设计的控制器能使AUV能够快速有效跟踪期望轨迹，具有较高的跟踪精度，而且能够有效地抑制外界干扰，达到理想的控制效果，具有较强的鲁棒性。