惯导系统两类冲击环境条件之间的等效转换

姚建军，闫红松，杨研蒙

(北京自动化控制设备研究所，北京 100074)

0 引言

在20世纪70年代以前，工程中普遍以冲量作为衡量冲击强度的标准，对作用时间相对较长的经典冲击关注较多。普遍认为[1]，虽然高频振荡冲击的加速度幅值较高，但是作用时间短、冲量很小，不足以对产品造成破坏。因此，航天产品的冲击强度最早以半正弦波形试验考核为主，后来又发展出了锯齿波、梯形波等经典波形，试验主要在各种跌落式冲击台、气动冲击台等装置上完成。早期航天产品的冲击试验也主要通过经典波形模拟设备完成[2-5]，对提高航天器结构和仪器设备的抗冲击可靠性起到了重要作用。但是，在经历了一系列高频冲击引起的问题后，人们发现航天器上的仪器设备或电子产品，对量级较大的高频更加敏感。实际测量数据分析表明，工程上遇到的冲击环境绝大多数以复杂振荡波形为主。因此，自20世纪70年代起，工程界对复杂冲击环境的破坏机理、模拟试验技术进行了大量的研究工作[6-8]。研究认为，复杂冲击的能量分布完全不同于半正弦等经典冲击，两者对产品的破坏损伤形式也不同。经典波形冲击具有较大的低频能量，高频能量不足；而复杂冲击具有较大的高频能量，而低频成分相对较低。因此，经典冲击对固有频率较低的大型部段结构的破坏作用较大，而复杂高频冲击对电子产品具有较强的破坏作用[9-11]。所以，从2009版GJB150A系列标准[12-13]发布以来，军用电子产品的冲击环境条件就很少再使用经典波形了。

由于每次复杂冲击过程的时间历程本质上是随机的，无法像经典冲击那样通过时间波形来描述冲击载荷。因此，工程上提出了冲击响应谱(Shock Response Spectrum，SRS)概念[14-15]，并以此作为描述冲击环境对产品的作用效果和试验条件的参数。根据定义，冲击响应谱是指将冲击激励施加到一系列线性、单自由度弹簧质量系统时，将各单自由度系统的最大响应值作为对应于系统固有频率的函数响应曲线(图1所示为GJB150A通常采用的冲击响应谱形)。由于缺失了相位信息，因此，冲击响应谱与时间历程不是一一对应的，一个冲击响应谱条件可以与无数个时间历程对应。理论上，同一个冲击响应谱可以通过无数个冲击波形来得到。这一特点为冲击模拟试验方法的选取提供了较大的灵活性，但同时也引起了不同模拟方法以及同一模拟方法的不同次试验对产品作用效果差异性较大的问题。相对而言，经典波形冲击试验的一致性要好得多。在惯导系统的研制过程中，如果试验的目的是验证其可靠性或环境适应性，那么试验输入条件的差异性是可以接受的；但如果试验的目的是为了验证设计参数的改进对系统在力学冲击环境条件下某项性能的影响，则期望试验输入条件的差异性越小越好，以确保试验状态的一致性。此时，经典波形冲击试验显然比冲击响应谱冲击试验更具优越性。如果能够在经典波形冲击试验条件与冲击响应谱冲击试验条件之间找到一种等效转换关系，使得经典波形冲击试验既可以较好地模拟冲击响应谱冲击试验对产品的作用效果，又能保持其良好的试验一致性，就可以有效地减小试验过程对试验结果分析带来的困扰，从而提高试验效果。本文基于这一目的开展了一些探索性的工作，提出了等效转换算法，并进行了试验验证。

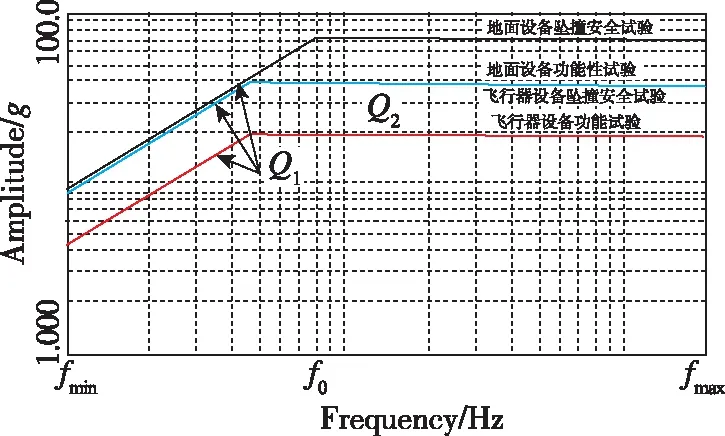
图1 冲击响应谱的典型谱形图Fig.1 Classical spectral chart of SRS

1 等效转换的基本准则

目前，国内外普遍采用等效损伤原则模拟复杂振荡型冲击环境[5-6,16-17]，其基本思想是：若产品在规定时间历程内，在冲击模拟装置产生的冲击激励作用下产生的冲击响应谱与实际冲击环境的冲击响应谱相当的话，就可以认为该产品经受了与实际冲击环境相当的冲击环境考核。本文也依据这一基本思想来研究不同冲击条件的等效转换关系。

分两种情况进行讨论：一种情况是惯导系统通过减振器柔性安装在弹体上，即惯导系统采用整体减振形式；另一种情况是惯导系统直接刚性安装在弹体上，不采用整体减振。对于前一种情况，研究[18-19]表明，当惯导系统的结构模态频率是减振系统刚体模态频率的4倍以上时，可看成是一个刚体，其冲击响应与单自由度系统的冲击响应一致，即采用整体减振的惯导系统可简化为一个单自由度系统。实践也证明，结构模态频率高于减振系统刚体模态频率4倍以上这个条件，对于绝大多数惯导系统结构而言是能够得到满足的。对于后一种情况，惯导系统可看成是一个多自由度系统。

1.1 整体减振系统的转换准则

惯导系统采用整体减振时，一般可以看成是一个单自由度系统。对于单自由度系统，无论试验条件是经典简单波形还是复杂振荡波形，系统冲击响应的时域形式均是周期与单自由度系统固有周期基本一致的衰减正弦曲线(参见图2)或准正弦曲线(参见图3)。由于冲击作用时间极短，响应曲线仅有寥寥几个峰谷，所以冲击对惯导系统的危害程度主要取决于响应曲线的最大峰(谷)值。因此，如果单自由度系统对经典波形冲击响应曲线的最大峰值与对冲击响应谱冲击响应曲线的最大峰值相当的话，就可以认为这两类冲击试验条件相当。根据冲击响应谱的定义，单自由度系统对某一力学环境响应的最大值即为该力学环境的冲击响应谱在与该单自由度系统固有频率相同的频率点处的谱值。所以，对于单自由度系统而言，2个力学环境条件的冲击响应谱只要在与该单自由度系统的固有频率相同的频率点上的谱值相当，即可认为它们对该单自由度系统的作用等效。此即当惯导系统可以简化为单自由度系统时，两类冲击试验条件相互转换的基本准则。

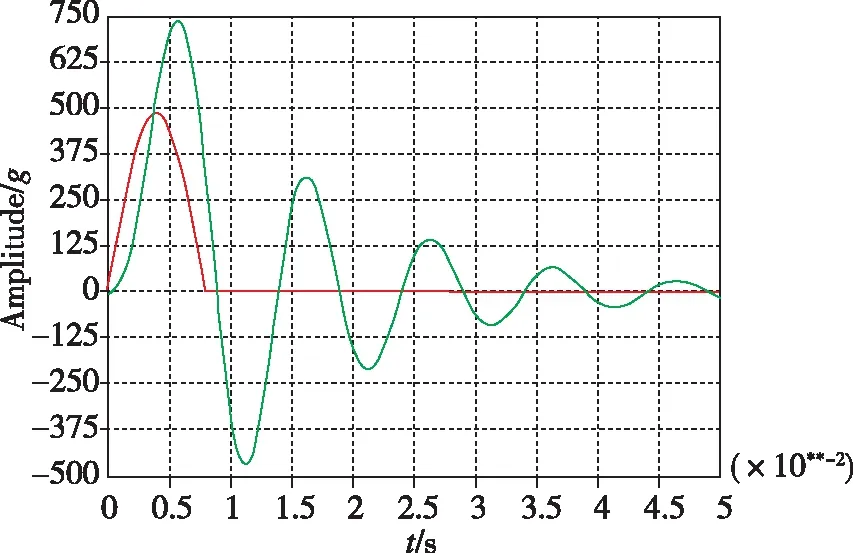
图2 单自由度系统在半正弦波冲击条件下的响应曲线(绿色)Fig.2 Response curve (green) of single degree of freedom system excited by half sinusoidal shock condition

图3 单自由度系统在冲击响应谱冲击条件下的响应曲线Fig.3 Response curve of single degree of freedom system excited by SRS shock condition

1.2 非整体减振系统的转换准则

非整体减振的惯导系统一般可以看成是一个多自由度系统。与可以看成是单自由度系统的采用整体减振方式惯导系统的冲击试验条件等效转换时，只要求单一频率点处等效不同，非整体减振设备的冲击试验条件等效转换，需要在多个频率点处同时等效，即要求两种试验条件在多个频率点处均具有相同的冲击响应谱值。由于不能事先确定需要在哪些频率点处等效，所以要求在试验要求的全频段内，2个冲击试验条件的冲击响应谱值均相当。此即当惯导系统不可以简化为单自由度系统时，两类冲击试验条件相互转换的基本准则。

2 等效转换方法

2.1 经典波形的冲击响应谱

经典冲击波形一般以时间历程曲线来表示。为寻求转换方法，首先需将它们转换为冲击响应谱的形式，以便进一步分析经典波形冲击条件与冲击响应谱冲击条件的差别。这里，除了给出半正弦波、后峰锯齿波、前峰锯齿波、梯形波等经典波形的冲击响应谱外，还补充给出了等腰三角波、矩形波等经典衍生波的冲击响应谱。为便于比较，约定经典波形的峰值均为100g，产生的冲击响应谱的转折频率均在200Hz，响应谱的阻尼值均为0.05。

图4～图9所示为根据冲击响应谱的基本概念，利用数值计算方法计算得到的各经典波形的最大加速度冲击响应谱。

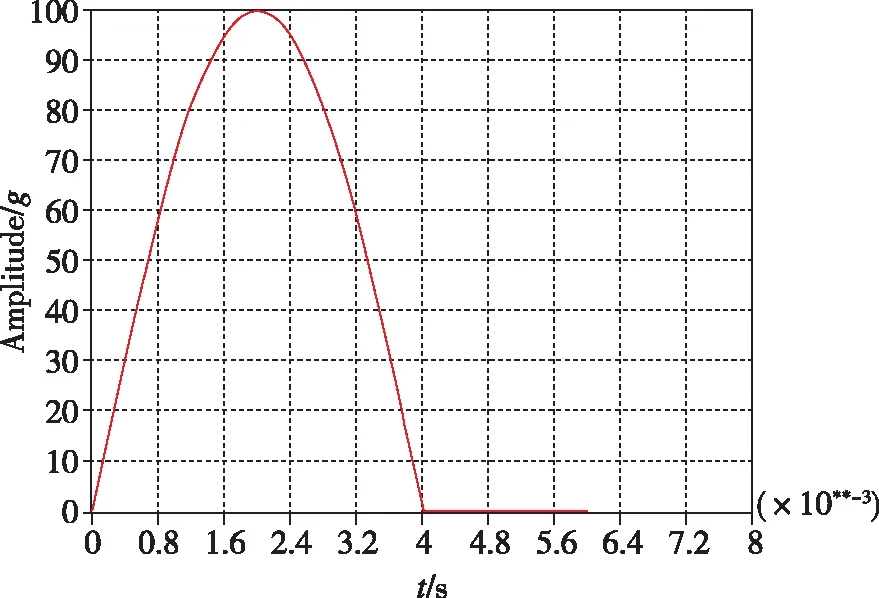
(a)半正弦波时域波形

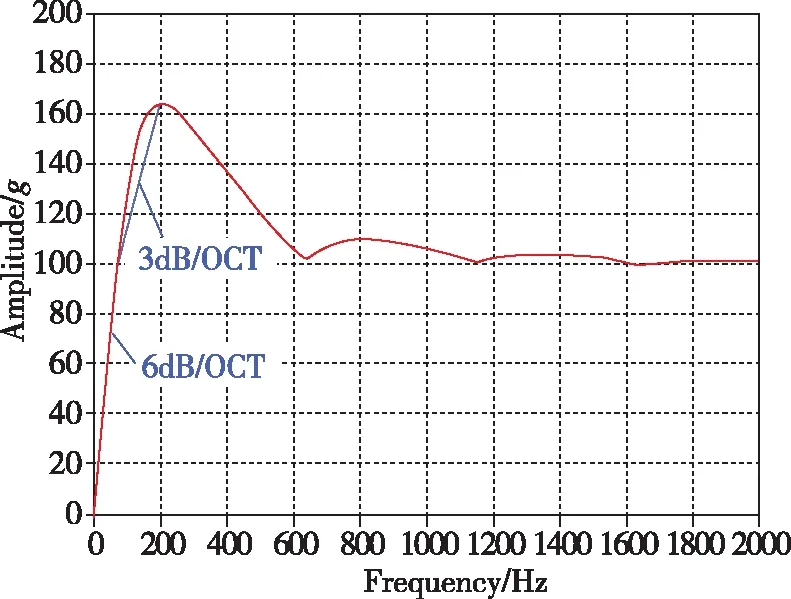
(b)半正弦波冲击响应谱图4 半正弦波形加速度冲击条件及其最大加速度冲击响应谱Fig.4 Half-sinusoidal wave acceleration condition and its maximum acceleration shock response spectrum

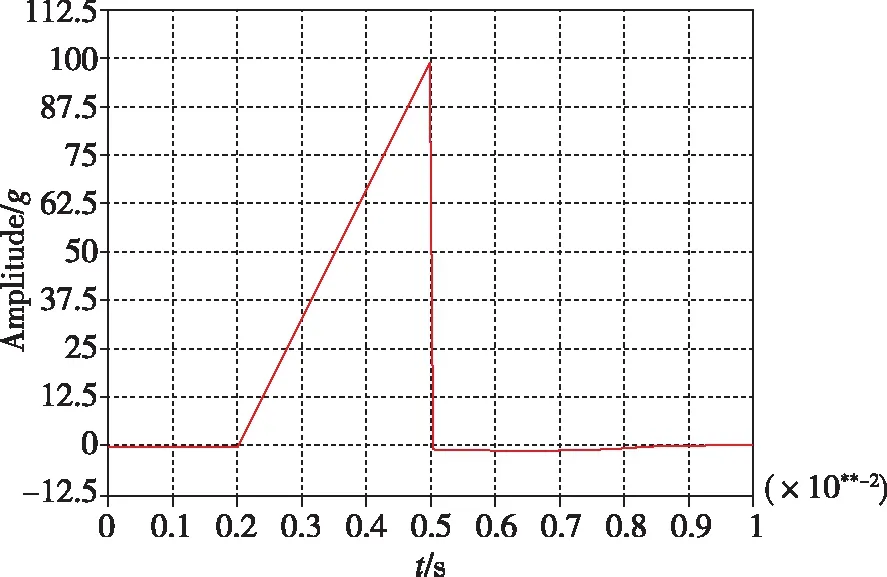
(a)后峰锯齿波时域波形

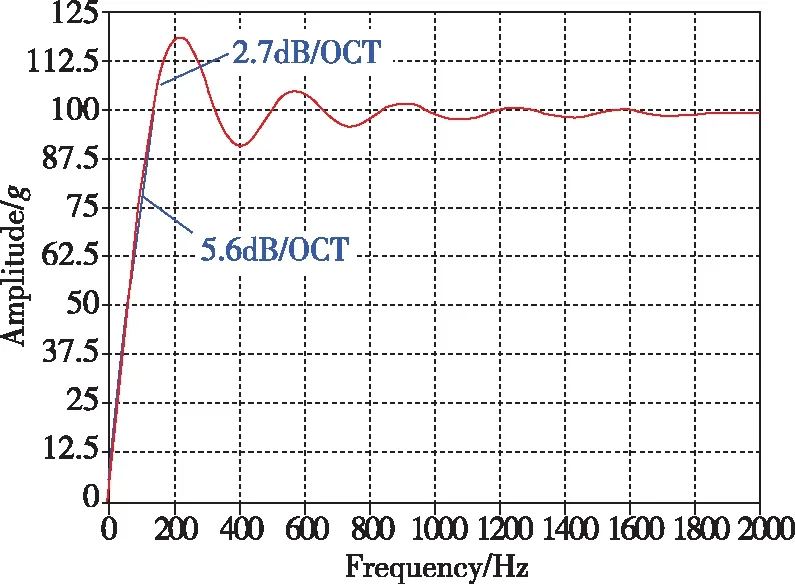
(b)后峰锯齿波冲击响应谱图5 后峰锯齿波加速度冲击条件及其最大加速度冲击响应谱Fig.5 Final peak sawtooth wave acceleration condition and its maximum acceleration shock response spectrum

(a)前峰锯齿波时域波形

(b) 前峰锯齿波冲击响应谱图6 前峰锯齿波加速度冲击条件及其最大加速度冲击响应谱Fig.6 Front peak sawtooth wave acceleration condition and its maximum acceleration shock response spectrum

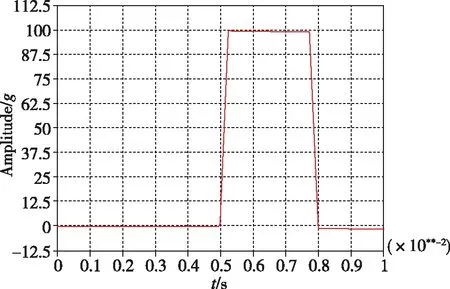
(a)梯形波时域波形

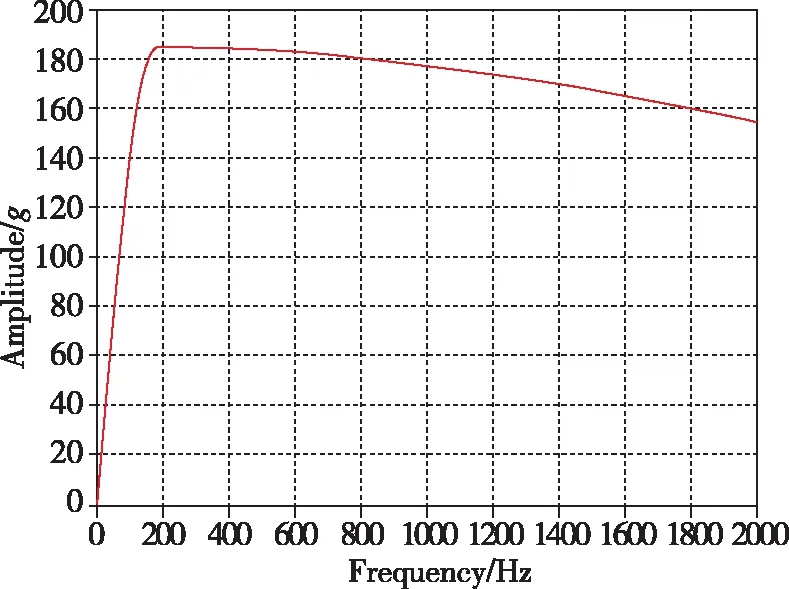
(b) 梯形波冲击响应谱图7 梯形波形加速度冲击条件及其最大加速度冲击响应谱Fig.7 Trapezoidal wave acceleration condition and its maximum acceleration shock response spectrum

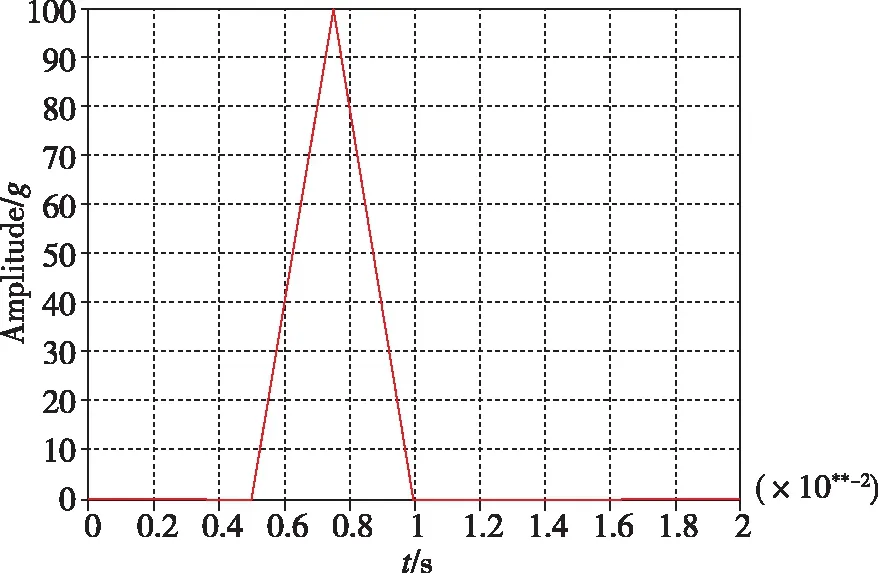
(a)等腰三角波时域波形

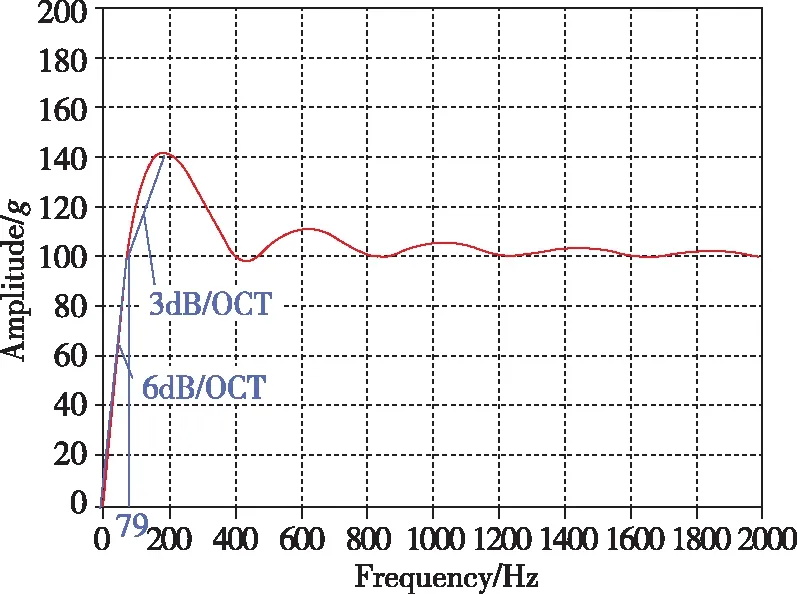
(b)等腰三角波冲击响应谱图8 等腰三角波加速度冲击条件及其最大加速度冲击响应谱Fig.8 Isoceles triangle wave acceleration condition and its maximum acceleration shock response spectrum

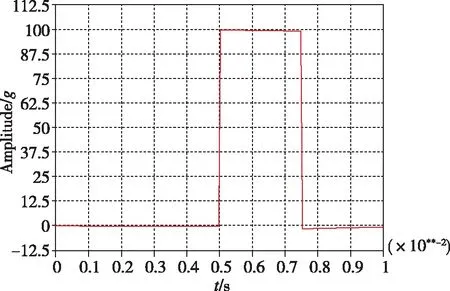
(a)矩形波时域波形

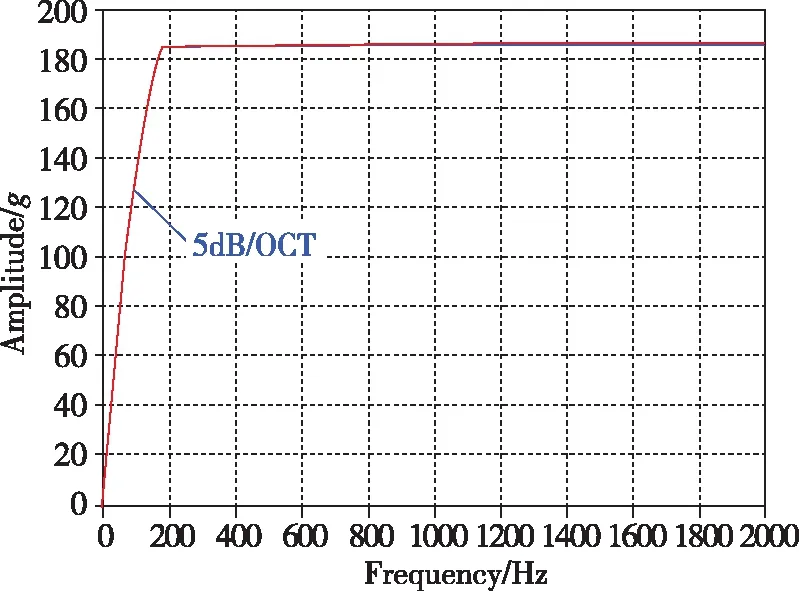
(b)矩形波冲击响应谱图9 矩形波加速度冲击条件及其最大加速度冲击响应谱Fig.9 Rectangular wave acceleration condition and its maximum acceleration shock response spectrum

2.2 整体减振系统的转换方法

理论上，使某一频率点处的谱值为某一固定值的谱形有无数种，所以可以用各种经典波形来等效，且每一种经典波形也有持续时间与峰值的无数种组合方法。为了充分利用现有试验条件，且便于计算等效输入条件，本文推荐用半正弦波形来进行等效。

等效方法：首先明确减振系统的固有频率，然后在冲击响应谱试验曲线中查找到(或者根据冲击谱试验条件计算得到)与该频率值相对应的谱值；令半正弦波冲击条件的冲击响应谱的最高峰值(参见图4(b))及该峰值频率分别与查找出的谱值及减振系统频率相等，据此计算半正弦波形的波峰值及半正弦波持续时间，计算方法见式(1)、式(2)。

(1)

(2)

式中，td为半正弦波形的持续时间；fd为减振系统的固有频率；Ap为半正弦波形的波峰值；S(fd)为冲击响应谱试验条件中频率fd处的谱值。

2.3 非整体减振系统的转换方法

对于非整体减振系统，需要在全频段内2个冲击试验条件的冲击响应谱值均相当才可以等效。观察2.1节中各经典波形的冲击响应谱，可以发现，矩形波最容易满足这一要求。矩形波的冲击响应谱在转折频率以后基本保持一条直线，这与GJB150A中要求的典型冲击响应谱完全一致；在转折频率之前的上升段，矩形波冲击响应谱的上升斜率约为5dB/OCT，与一般遇到的冲击响应谱的上升段斜率误差不超过3dB，满足GJB150中规定的试验误差要求。此外，非整体减振惯导系统的固有模态频率一般位于冲击响应谱平直段谱线所覆盖的频率范围内，所以，上升段谱值误差的影响将会更不显著。因此，本文采用矩形波来等效非整体减振设备的冲击响应谱试验条件。

等效方法：首先明确冲击响应谱试验条件的转折频率、平直段谱值，然后据此计算矩形波的持续时间和峰值，计算方法见式(3)、式(4)。

(3)

(4)

式中，td为矩形波的持续时间；f0为冲击响应谱试验条件的转折频率；Ap为矩形波的波峰值；S(f0)为冲击响应谱试验条件平直段的谱值。

2.4 验证

无论是整体减振系统所采用的半正弦波等效转换方法，还是非整体减振系统所采用的方波等效转换方法，转换公式都是基于数值试验结果归纳得出的，可以认为在数学上是精确的。但是，在物理试验中，两种试验结果的一致性就没有这么理想。前面已经说过，这主要是由于冲击响应谱试验的离散性造成的。通过对大量试验结果进行比较分析，发现：按照本文方法转换得到的经典波形冲击试验结果接近多次冲击响应谱冲击试验结果的平均水平。

3 总结与讨论

冲击响应谱比经典冲击波形能够更加真实地表现实际冲击环境的复杂性，有助于促进惯导系统等航天电子设备地面试验真实性的提升。毋庸置疑，GJB150A采用冲击响应谱的形式来表示各类冲击试验条件是有其进步意义的。但冲击响应谱形式的冲击试验条件也有不足，最明显的是试验结果的差异性较大。这给产品研制过程中的试验研究带来很大困扰，在很多情况下，甚至无法分辨试验结果的变化到底是由于设计参数的改变造成的，还是由于试验条件的离散造成的。为了解决这个问题，本文提出了采用经典波形等效冲击响应谱的基本准则和方法，经实践验证是有效的。基于此，本文倡议，当采用试验方法研究设计参数或算法的改变对惯导系统在冲击环境条件下的性能影响时，最好采用等效的经典波形冲击试验方案，以避免由于试验条件的波动对试验结果造成的干扰；当验证惯导系统对冲击环境条件的适应性或产品可靠性时，最好采用冲击响应谱试验方案，以确保地面试验的真实性。