一种新的基于ANSYS的机翼挠曲变形建模方法

张雪燕，赵 剡，司 帆，耿澄浩，张志东

(北京航空航天大学仪器科学与光电工程学院，北京 100191)

0 引言

在现代作战行动中，武器的精确击打能力尤为重要。作为未来信息化战争中争夺海陆空天的主战武器，高精度制导武器是当今世界各军事强国的研究热点。因此，对弹载捷联惯导系统进行快速高精度的传递对准非常必要[1]。传递对准作为惯性导航系统的一种初始对准技术，通常利用高精度主惯导提供的基准信息来对中、低精度的子惯导进行对准，以缩短对准时间和提高对准精度。由于子惯导离主惯导距离较远，在湍流、气动载荷等的影响下，平台运动带来的挠曲变形是影响机载武器传递对准性能的重要因素，因此,必须补偿对姿态有重要影响的挠曲变形[2]。

工程上对动态挠曲变形补偿最简单的方法是在模型中注入噪声[3]。通过将动态挠曲变形建模为白噪声过程，以牺牲精度为代价，可以减少系统状态变量维数，从而减少滤波计算量。

另一种常用的补偿挠曲变形的方法是将动态挠曲变形建模为马尔可夫随机过程，这种方法需要机翼弹性变形数据以确定随机模型参数。文献[4]将机翼挠曲变形建模成二阶马尔可夫过程，加入到速度加角速度匹配传递对准模型中，将挠曲变形角及挠曲变形角速度扩展为状态变量进行滤波。但模型的有关参数全凭经验设定，缺乏适用性。文献[5]使用主、子惯导的测量数据差值作为挠曲变形建模的随机过程序列，但这种方法忽略了主、子惯导测量数据中包含的其他误差。文献[6]利用激光测量数据获取挠曲变形随机过程序列，并利用最小二乘法辨识模型参数，但该方法工程实施复杂。文献[7]运用ANSYS辅助力学建模的方法,建立了模拟机翼杆挠曲运动模型，但其使用的悬臂梁结构与实际机翼相差甚远。

本文提出了一种飞机机翼挠曲变形的建模方法，并通过有限元分析法(Finite Element Analysis,FEA)获取的机翼变形数据对模型的参数进行在线辨识。该方法的优点在于可以根据实际中不同机翼的结构建立不同的机翼模型，结合ANSYS获取的机翼变形信息，给出了模型中的具体参数，从而使该模型与机翼真实运动情况更相符。

1 机翼结构外型的设计与建模

1.1 机翼相关参数确定

现代高空无人机普遍采用大展弦比机翼。研究表明，大展弦比机翼因具有高升阻比的特性，所以常作为高空长航时飞行器的机翼。同时，大展弦比机翼的质量较小，结构细长，因而柔性很大。飞机在飞行时，柔性机翼在气动载荷和自身重力的作用下会产生相应的气动变形，发生显著的弯曲和扭转变形，这有利于进行机翼的挠曲变形分析。因此，本文针对大展弦比平直翼进行了建模与研究。

机翼面积可由式(1)得到[8]：

S=b2/A

(1)

其中，b是翼展长，S是机翼面积，A是展弦比。

由于是平直翼，跟梢比n=1，则弦长为：

(2)

通过查阅手册，结合上述公式，确定了机翼的主要参数，如表1所示。

表1 机翼的主要参数Tab.1 Primary parameters of the wing

1.2 机翼翼型选择

翼型的气动特性直接影响着机翼、飞机的气动特性。基于无人机设计要求及机翼主要技术指标，论文初步选用NACA2412翼型。本文中翼型的数据由机翼设计软件Profili获得，翼型图如图1所示。

图1 NACA2412翼型图Fig.1 The airfoil diagram of NACA2412

高空长航时无人机，由于飞行高度大，空气逐渐稀薄，导致飞行动压比较小。因此，高升力系数是其机翼翼型的主要特征。由于不同雷诺数下相同翼型的气动性能会有较大不同，所以需先计算机翼的雷诺数，查看在这一雷诺数下机翼的性能。雷诺数的计算公式为:

Re=ρvr/η

(3)

其中，ρ为空气密度，v为无人机飞行速度，r为空气流过机翼的长度，η为空气动力黏度。

查阅资料可知，海平面4000m以上高空的空气密度ρ=0.8kg/m3，无人机飞行速度约为v=100km/h，空气流过机翼的长度约为400mm，空气动力黏度η=1.7×10-5(N·s)/m2。代入式(3)中可得机翼雷诺系数约为5×105。在此雷诺数时，翼型的升阻特性及力矩特性等性能参数曲线如图2所示。图2中，Cl是升力系数，Cd是阻力系数，Cm是力矩系数，α是迎角。

图2 NACA2412翼型性能参数曲线Fig.2 Performance parameter curves of NACA2412

由图2可以看到，飞机在失速前有较高的升阻比和良好的力矩拐折特性。因此，在此雷诺数条件下，翼型NACA2412具有良好的空气动力特性，这说明论文选取翼型NACA2412是合理的。

1.3 机翼结构的CATIA建模

要能在后续研究中运用有限元分析精准地解决实际工程问题，就必须建立一个合理并能最大程度反映机翼实际工作情况的简化模型。因此，确定了薄蒙皮、双翼梁、多肋板式机翼结构布局。蒙皮置于机翼外部，承载气动载荷并传递给翼梁和翼肋。翼梁是机翼纵向核心承力组件，承担所有的拉、压应力。翼肋均布于翼梁之间，纵横交错，转变载荷方向，并将载荷均匀地作用于机翼上，使机翼结构不发生过大的变形[9]。

蒙皮厚度为2.5mm；前梁直径为15mm，位于25%翼弦处；后梁直径为12mm，位于65%翼弦处。肋距设为517mm，厚度为2.5mm。翼型数据由Profili共享接口导入CATIA进行建模，机翼的内部结构如图3所示。

图3 机翼模型的内部结构Fig.3 Internal structure of the wing model

机翼的蒙皮直接由翼型轮廓拉伸形成，如图4所示。机翼的最终装配图如图5所示。

图4 机翼模型的蒙皮结构Fig.4 Skin of the wing model

图5 机翼模型的最终装配图Fig.5 Final assembly diagram of the wing model

其中，蒙皮较薄，采用轻质铝合金制作，降低了机翼的结构质量。翼梁、翼肋采用钛合金，以保证足够的刚度。

2 基于FEA的机翼变形信息获取

2.1 基于流体动力学的机翼结构绕流分析

机翼结构所承受的载荷主要为结构质量力、导弹重力和空气动力载荷。机翼在飞行状态下所受的空气动力载荷可以通过流体动力学分析得出。本文应用Fluent软件建立了载机飞行时的流场域模型，是长宽高分别为3.5m×0.4m×0.8m的长方体，其大小约为机翼结构的10倍。空间流场域的网格划分如图6所示。

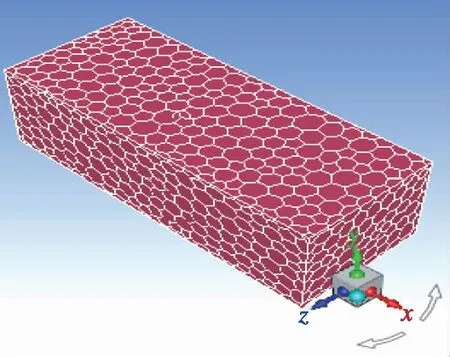
图6 流场域网格示意图Fig.6 Grid meshing of flow field

模拟中载机的飞行高度为H=4000m，飞行速度v=0.8马赫，机翼的攻角为5°。通过显式求解方程，选择通量差分法为求解方式，流体材料选为空气，可以得到机翼表面的压力分布云图，如图7所示。可以看到，机翼下表面所受压力大于机翼上表面，这也是机翼产生升力的原因。该分析结果可以辅助设置瞬态动力学分析中机翼结构的受力加载。

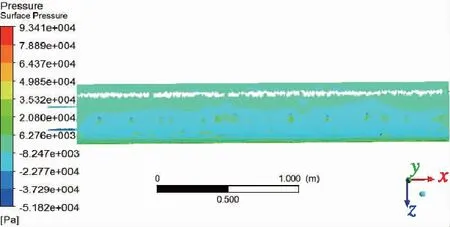
(a) 机翼上表面

(b)机翼下表面图7 机翼表面压力分布云图Fig.7 Pressure distribution diagram of the wing surface

2.2 模态分析

模态分析，是研究结构动力特性的一种方法。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。模态分析的最终目标是识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报、结构动力特性的优化设计提供依据[10-11]。

机翼结构模型的网格划分如图8所示。

(a) 蒙皮

(b)翼梁和翼肋图8 机翼模型的网格划分示意图Fig.8 Grid meshing of the wing model

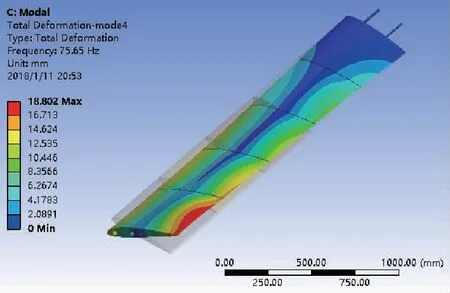
本文在模态分析时采用Block Lanczos计算方法。由于高阶的模态频率过高，很难被激励。因此，在计算结构固有动力特性时，仅计算低阶模态即可。本文利用ANSYS软件计算了机翼模型的前四阶模态，这样既提高了计算的效率，同时也不影响计算的准确性。表2列出了机翼前四阶的固有振动频率及最大变形位移。图9所示为机翼的前四阶振型图。

表2 机翼前四阶的固有频率及各阶最大位移Tab.2 Inherent frequencies and the largest deformation of the first four orders

(a) 第一阶

(b)第二阶

(c)第三阶

(d)第四阶图9 前四阶振型图Fig.9 Modal shapes of the first four orders

从分析结果可以看出，载机挂弹飞行时机翼各阶模态的固有频率，且模态阶数越高，机翼的固有频率越高。从图中可以看出，第一、二、三阶振动模态下，机翼主要发生弯曲变形；第四阶振型发生了明显变化，机翼主要发生扭转变形。并且，机翼变形位移沿半翼展方向呈增大趋势，最大变形位置在翼尖。

由于飞机飞行时，外界激励更容易接近低阶频率[13]。而模态分析的结果显示，飞机前三阶模态的固有频率较低，更容易被激励。因此，在后续对机翼的挠曲变形进行瞬态动力学分析时，考虑到前三阶模态主要发生弯曲变形，论文对机翼绕Y轴发生的弯曲变形进行分析与建模。

2.3 瞬态动力学获取机翼变形观测量

瞬态动力学分析是用于确定结构在承受时变载荷时的动力学响应的一种方法。要获得机翼上导弹不同挂点在时间序列上的变形信息，可以运用ANSYS通过瞬态动力学分析获得。

飞行中，机翼受到的载荷主要有：机翼结构质量力、导弹重力与空气动力载荷。将导弹的重力加载到悬挂面上。空气动力载荷是机翼受到的主要外载荷，将此力沿翼展方向等大地施加到蒙皮表面。

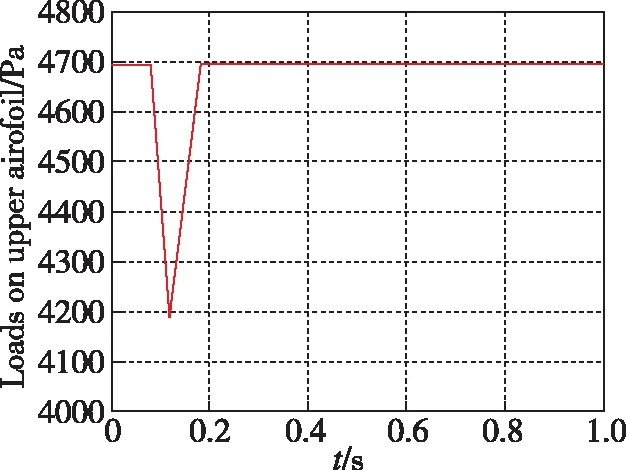
通过绕流分析，在Fluent软件中模拟得到了机翼的载荷分布[14]。根据绕流分析结果中的压力分布云图，对得到的数据进行了一定的规整化处理，处理后的机翼所受的动态载荷如图10所示[14]。

(a) 上翼面

(b) 下翼面图10 机翼表面受力加载图Fig.10 Loading diagrams of the wing surface

在机翼表面按图10所示进行加载，同时机翼上受到的导弹质量集中力在发射时也消失。对此力采用阶跃加载法，在初始时刻力的大小为1000N，计算时间为0.001s。对机翼进行瞬态动力学分析，采用缩减法求解，分析结束后得到的机翼总变形图如图11所示。

图11 机翼总变形图Fig.11 Total deformation of the wing

与模态分析的结果一致，机翼主要发生弯曲变形，翼尖处变形程度最大，翼根处变形程度最小。此外，机翼后缘处有轻微扭转变形。机翼的最大变形位移是71.911mm。

在变形程度最大的翼尖取一个节点，观察该节点绕Y轴的挠曲变形角变化，如图12所示。可以看到，在导弹发射后，该节点绕Y轴的角度有明显的变化。机翼绕Y轴先向上变形至上峰值2.76°，再反向弯曲变形至约1.08°。0.4s后，机翼的挠曲变形角在1.5°左右做振荡变化。这是因为导弹在发射后，机翼所受的重力、气动载荷重新达到一个近似的平衡状态。横向分析20%、40%、60%、80%、100%半翼展处5个位置的位移响应曲线，如图13所示，其变形规律基本一致。并且，机翼变形位移沿半翼展方向逐渐增大，最大位移位于翼尖位置。这与模态分析的结果基本一致。

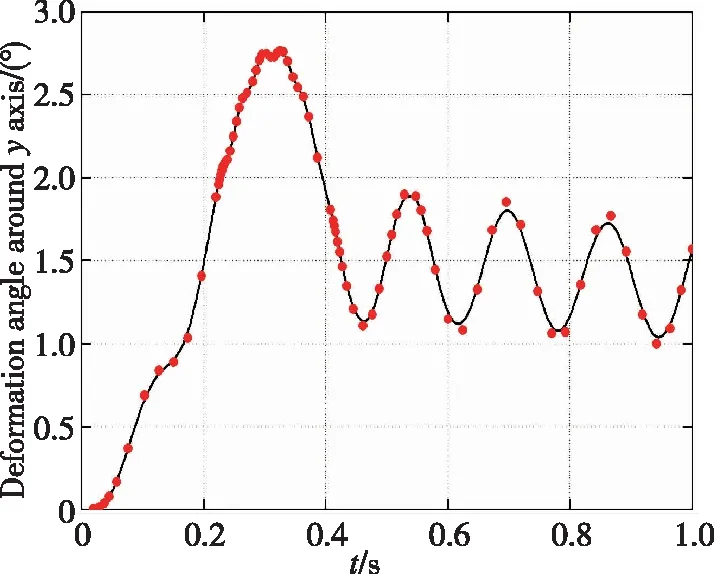
图12 Y向机翼挠曲变形角Fig.12 Deformation angle of the wing around Y axis

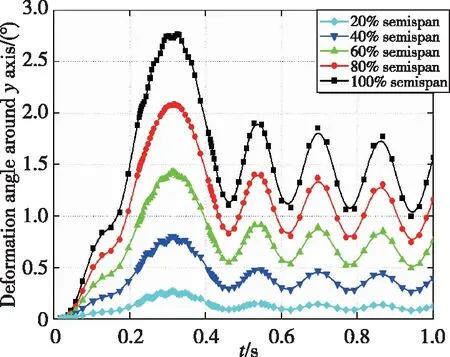
图13 不同位置Y向机翼挠曲变形角Fig.13 Deformation angle around Y axis at different displacement

3 机翼弹性变形建模

利用第2节获得的机翼上导弹不同挂点在时间序列上的机翼变形数据，采用ARMA模型进行建模。ARMA模型是研究时间序列的重要方法。它由自回归模型(简称AR模型)与滑动平均模型(简称MA模型)为基础混合构成。实际中，当n充分大的时候，ARMA(p,q)模型可用有限阶AR(n)模型逼近到任意精度。对于AR(n)模型，有：

(4)

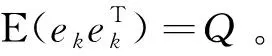
式(4)写成向量的形式为：

λk=Hkβ+ek

(5)

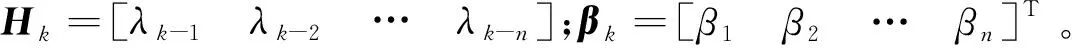
即可通过获取的机翼变形信息，利用AR(n)模型进行建模。对于式(5)中β的估计，采用一种改进的卡尔曼滤波算法进行参数辨识[15]。β的递推算法为：

(6)

定义了一个准则函数：

(7)

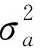
(8)

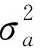
表3 绕Y轴机翼弹性变形建模Tab.3 Modeling of the wing flexure deformation around Y axis

根据适用性检验结果，可以将AR(2)模型用来加入到传递对准模型中，在传递对准中考虑机翼的弹性变形。

4 结论

针对传递对准中机翼弹性变形建模困难的问题，本文提出了一种基于有限元分析法获取机翼变形观测量并进行弹性变形建模的方法。论文的具体实现主要有以下3个方面：

1)与传统研究将机翼简化为悬臂梁，并对其力学性能等作近似处理不同，本文建立了薄蒙皮、双翼梁、多肋板式机翼结构模型，更贴近实际机翼结构模型。该方法可以根据实际中不同的载机型号，实现对不同机翼结构的建模，更具工程应用价值。

2)利用有限元分析方法，论文通过流体动力学中的绕流分析，得到了机翼在飞行时的压力分布云图，并以此为依据在后续研究中对机翼进行受力加载。根据模态分析的结果，确定了以机翼绕Y轴的弯曲变形为主要研究对象。最终，利用瞬态动力学分析实现了机翼结构不同挂点处的变形信息获取。

3)利用前一步获取的任一待发射导弹挂点处在时间序列上的机翼变形数据，采用AR(2)模型来简化ARMA(p,q)模型进行机翼弹性变形的建模，并利用信息对准模型的适用性检验确定模型的阶数。后续研究中，可以通过仿真试验验证该建模方法对提高传递对准精度的有效性。