2.1.1数轴上的基本公式

辽宁省沈阳市辽中区第一高级中学 陈中华

指导思想与理论依据

本课的教学设计基于“人人都能获得必要得数学”即平等性的考虑，坚持面向全体学生，努力设计“适合学生发展得数学教育”，体现“人人学数学”，“不同的人学不同的数学”的理念。教学中强调“培养学生情感、态度与价值观”的重要性，注重引导学生主动地进行探索，从而帮助学生树立正确的数学观，但又与教师的设计问题与活动的引导密切结合，强调“活动”的内化，即在头脑中实现必要的重构或认知结构的重组，从而引起真正的数学思维，提高思维的效益。通过联系学生的生活实际使其真正感到数学是有意义的，一方面培养学生的社会意识，明确肯定“日常数学”的合理性等，另一方面，再调动学生生活经验的同时，又应努力帮助他们清楚地去熟悉生活经验并上升到“学校数学”的必要性。

教学目标(含重、难点)

一、教学目标

1.知识与技能

(1)理解实数与数轴上点的一一对应关系及实数运算在数轴上的几何意义.

(2)理解向量及其相等的概念，掌握数轴上向量加法的坐标运算及数轴上两点间的距离公式.2.过程与方法

(3)通过对初中所学的数轴知识的复习，明确数轴上的一点所表示的实数就是这点在数轴上的坐标，并借此引入向量的概念.培养学生观察、探索的能力，运用数学语言表达的能力，数学交流与评价的能力.

(4)通过直观分析、计算验证引入基本公式AC＝AB＋BC，这个公式是解析几何的基本公式，务必理解并掌握.

2.情感、态度与价值观

(1)学会观察发现、类比、猜想和实验探索，培养创新能力和动手能力.

(2)培养树立辩证统一的观点，形成严谨的科学态度和求简的数学精神.

二、教学重点、难点

重点：数轴上的基本公式.

难点：向量的坐标或数量

难点突破：建立向量和实数的对应.

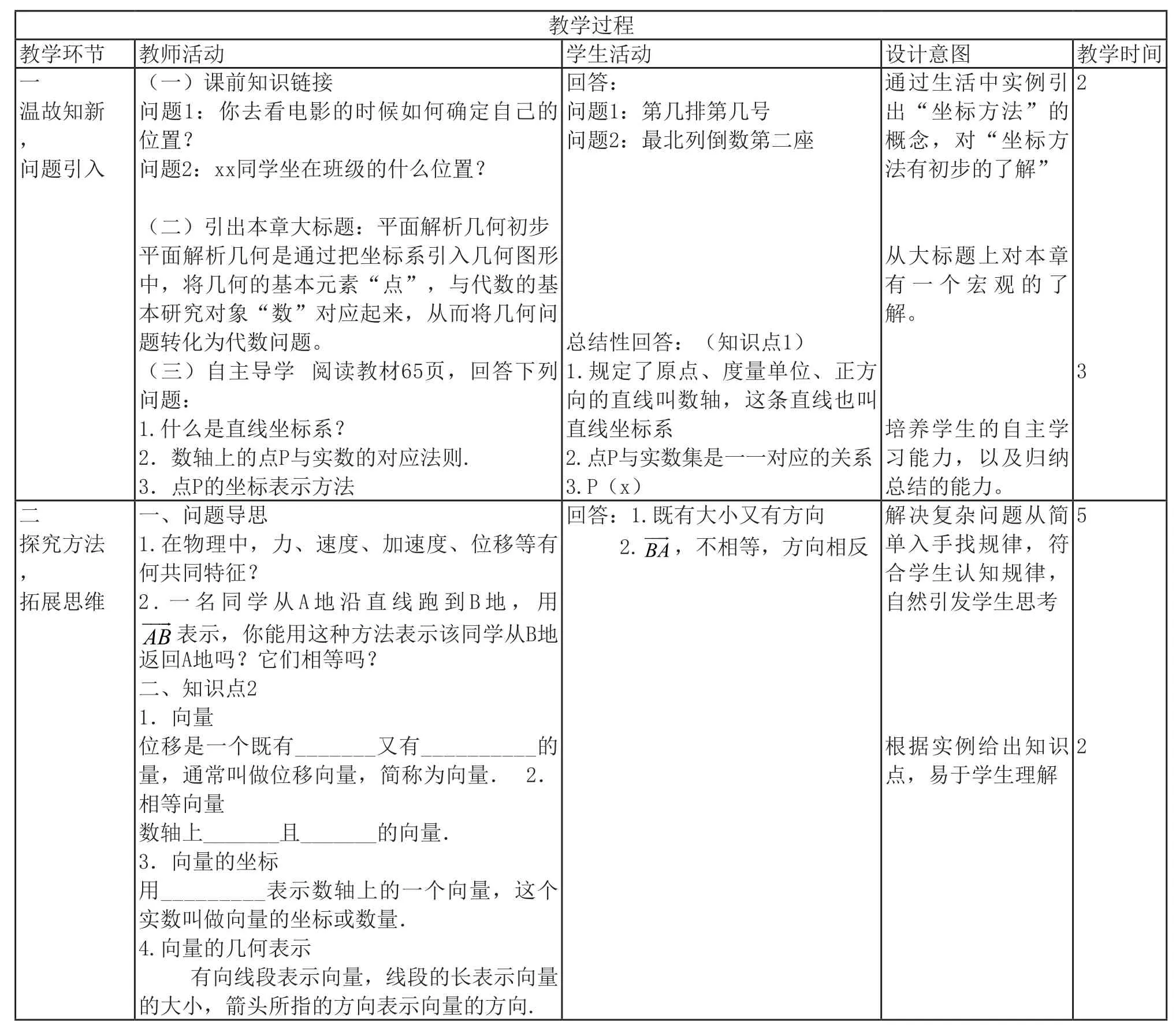
教学过程教学环节 教师活动 学生活动 设计意图 教学时间一温故知新，问题引入（一）课前知识链接问题1：你去看电影的时候如何确定自己的位置？问题2：xx同学坐在班级的什么位置？（二）引出本章大标题：平面解析几何初步平面解析几何是通过把坐标系引入几何图形中，将几何的基本元素“点”，与代数的基本研究对象“数”对应起来，从而将几何问题转化为代数问题。（三）自主导学 阅读教材65页，回答下列问题：1.什么是直线坐标系？2.数轴上的点P与实数的对应法则.3.点P的坐标表示方法回答：问题1：第几排第几号问题2：最北列倒数第二座通过生活中实例引出“坐标方法”的概念，对“坐标方法有初步的了解”2从大标题上对本章有一个宏观的了解。总结性回答：（知识点1）1.规定了原点、度量单位、正方向的直线叫数轴，这条直线也叫直线坐标系2.点P与实数集是一一对应的关系3.P（x）3培养学生的自主学习能力，以及归纳总结的能力。二5探究方法，拓展思维一、问题导思1.在物理中，力、速度、加速度、位移等有何共同特征？2.一名同学从A地沿直线跑到B地，用回答：1.既有大小又有方向2.■■■→BA ，不相等，方向相反解决复杂问题从简单入手找规律，符合学生认知规律，自然引发学生思考表示，你能用这种方法表示该同学从B地返回A地吗？它们相等吗？二、知识点2 1.向量位移是一个既有_______又有__________的量，通常叫做位移向量，简称为向量.2.相等向量数轴上_______且_______的向量.3.向量的坐标用_________表示数轴上的一个向量，这个实数叫做向量的坐标或数量.4.向量的几何表示有向线段表示向量，线段的长表示向量的大小，箭头所指的方向表示向量的方向.■■■→AB根据实例给出知识点，易于学生理解2

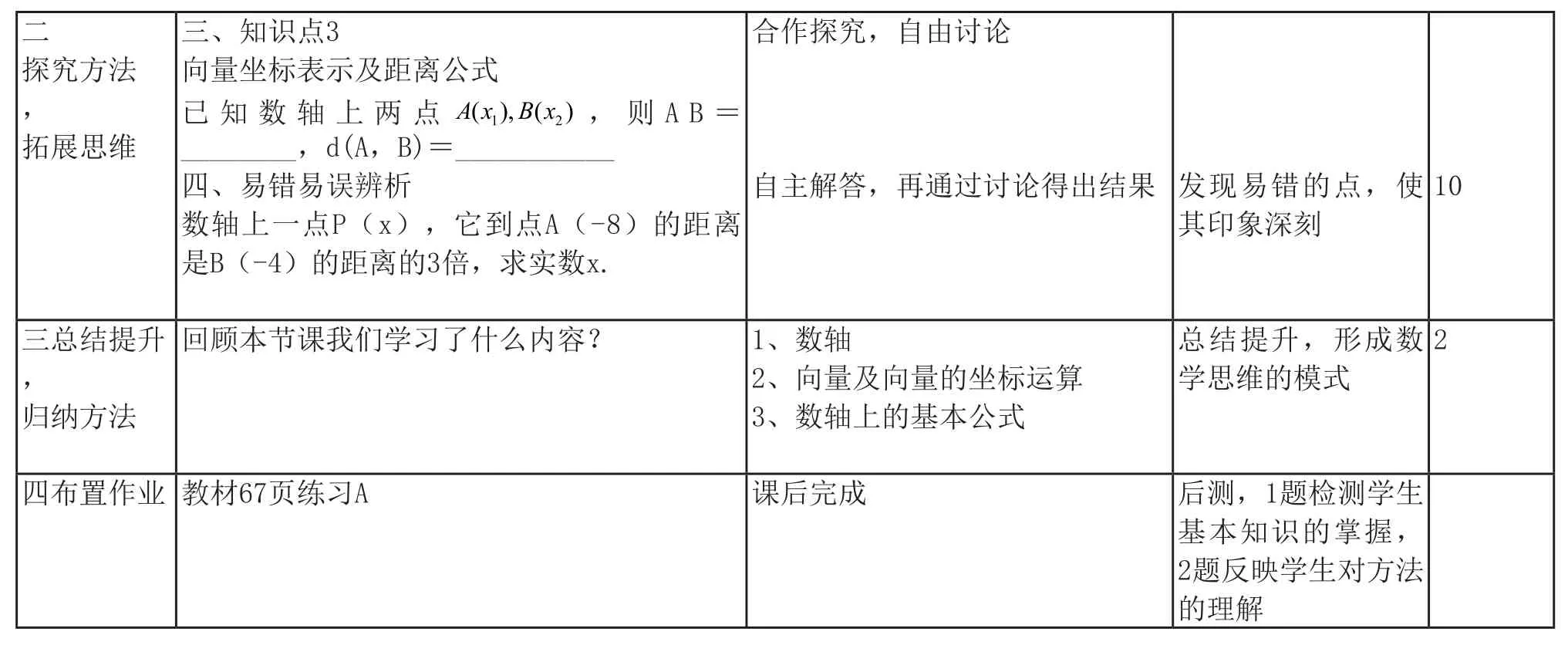
二合作探究，自由讨论探究方法，拓展思维三、知识点3向量坐标表示及距离公式已知数轴上两点 ，则A B＝________，d(A，B)＝___________四、易错易误辨析数轴上一点P（x），它到点A（-8）的距离是B（-4）的距离的3倍，求实数x.A x B x(),()1 2自主解答，再通过讨论得出结果 发现易错的点，使其印象深刻10三总结提升，归纳方法回顾本节课我们学习了什么内容？ 1、数轴2、向量及向量的坐标运算3、数轴上的基本公式总结提升，形成数学思维的模式2四布置作业 教材67页练习A 课后完成 后测，1题检测学生基本知识的掌握，2题反映学生对方法的理解