解物质的量计算的认知模型研究

浙江省台州市灵石中学 洪益玲

一、前言

2016年9月，随着“中国学生发展核心素养”的正式发布，教育部印发了高中各科课程标准。《普通高中化学课程标准（2017版）》明确要求，学生能认识化学现象与模型之间的联系，能运用多种认知模型来描述和解释物质的结构、性质和变化，预测物质及其变化的可能结果。

由于物质的量概念本身的抽象性，使其成为高中化学的教学难点。现在的学生综合解决问题的能力不强，面临未知、不熟悉的问题情境时，选择放弃的比较多。因此，本文选择了物质的量计算这一内容进行研究，试图建立认知模型帮助学生解决复杂化学问题。

二、认知模型的构建基础

“认知模型”这一个术语起源于计算机科学领域，在计算机科学领域是指“人类认知过程中计算机模型”，在认知心理学中则被用来简化描述人的认知过程。通过以上分析看出：认知模型是指依据物质及其变化的信息建构模型，建立解决复杂化学问题的思维框架。

高中生正处于生理和心理发展的高峰期，他们积极、热情、真挚、实事求是，单缺少社会经验，想法单纯，容易轻信别人的看法。他们的思维发展还不够成熟，无法建立自己的认知结构，遇到问题缺乏理智，思想方法上较多片面，看问题大多流于事物的表面，不够全面；缺乏主动思考，没有独立解决问题的能力。他们满足于现成结论，对别人的意见容易相信，盲从。相当多的高中生不能多层次、多角度地全面认识事物和处理问题，思路狭窄，不能用科学的视角去分析解决问题，不能看到事物的本质。

高中化学课程学习知识点很多，难度较大。在知识积累不断增多时，学生无法做到举一反三、触类旁通，思维存在混乱状态，严重影响他们学习的动力和效率。特别是对于处于信息，掌握知识本身并不是最重要的，更重要的是掌握运用知识的方法，这就要求培养高中生能依据物质及其变化的信息建构认知模型，以解决复杂的化学问题。因此，帮助学生构建认知模型，能加快知识掌握和问题解决的速度，减少或避免高中生思维的盲目性，提高学习的效率。学生通过建立相应的认知模型顺利解决现实问题，才能更好地适应当今社会的发展。

三、解物质的量计算的认知模型构建

1.认知模型建构在解物质的量计算中的作用

以物质的量为核心的化学计算是高中化学计算教学的核心。由于此类计算类型复杂、牵涉到的知识面广，学生往往对有关计算不能融会贯通，做题时就题论题，得不到好的教学效果，成为化学计算教学中的一个难点。我认为，突破此难点的关键是根据物质的量知识结构建立起认知模型，才能举一反三，事半功倍。

做题时需要先分析问题，明确问题的特点和要求，再依据问题的特征，结合自身的认知水平，构建认知模型，然后依据模型去解决复杂问题。

2.解物质的量计算的认知模型的构建

物质的量计算为“读题——析题——初建模型——解题——完善模型”的过程，过程中构建模型是解决问题的关键所在，由此构建了根据物理量之间换算模型、根据化学式计算模型、根据化学方程式计算模型。

（1）根据物理量之间换算模型

物质的量（n）、摩尔质量（M）、物质的量浓度（c）、气体摩尔体积（Vm）和稀溶液中溶质物质的量浓度之间的换算，基本上是一个已知量计算另一个未知量，通过多个公式进行换算，就能完成简单物质的量的计算。

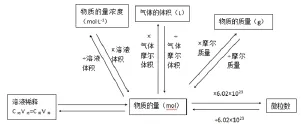
（2）根据化学式计算模型

对于一个化学式AaBb，n（A）：n（B）=a：b，先将已知微粒的物理量进行换算，再根据各微粒之间的物质的量之比等于微粒个数之比的关系，进行计算。

（3）根据化学方程式计算模型

对于一个化学反应，先找到反应物和生成物的始态和终态——算出各组成物质的量的变化量——利用各组分物质的量变化之比等于方程式系数之比建立关系式。

3.解物质的量计算的认知模型的检验

构建认知模型有助于学生理解知识的本质，掌握解决问题的“套路”，培养学生举一反三的能力，提升学生的化学核心素养。解物质的量计算的认知模型将解题方法程序化，将复杂问题简单化，这样有利于学生快速、准确解题，提高得分率，最终会起到事半功倍的效果。

通过多种物质的量认知模型的构建，既能解决有关物质的量计算问题，又有助于提高学生的模型构建能力、类比迁移能力、信息分析处理能力和逻辑思维能力，提升学生的化学核心素养。总之，一个好的认知模型应该是：能够把复杂凌乱的内容化繁为简，把抽象难以观察的内容显化，能够帮助学生掌握知识本质和核心。

四、认知模型对化学教学的启示

解物质的量计算的认知模型对教学过程中问题设计、认知诊断及教学干预具有重要意义。

认知模型是研究学生化学学习过程中的一种有效手段。问题解决是一个复杂的过程，心理学、认知科学、认知神经科学都对该领域进行了研究，但因为视角不同，都无法也不可能对问题解决的实际过程详细描述。问题解决的认知过程无法直接获取，通过构建认知模型来获取。

通过模型可以看出，问题解决问题由几个阶段所构成，每个阶段包含有若干个内部加工的过程。要产生一定的学习结果，在设计问题时应依内部加工过程为依据。例如：设计问题时，应该考虑化学学科的特殊性以及高中生的认知特点，突出问题情境与学生生活实际相联系。

认知模型能够引导学生自己去探索建模的过程，初步领会模型的思想和方法，从而提高学生的创新能力，养成良好的化学思维品质，使学生看到不同的化学，学到有用的化学。