线性二次型调节器算法研究

朱云昊，汤卫红

（海装西安局 西安 710068）

0 引言

四旋翼飞行器结构简单、轻便易携带、能垂直起降、自由度高，是一种良好的验证飞行控制算法的平台，无人机飞行控制系统是其能够安全、有效地完成复杂战术、战略使命的基本前提，因此，研究无人机的自动飞行控制技术具有十分重要的现实意义。目前线性二次型调节器（LQR）在处理可精确数学描述的对象时取得了很大的成功，在提高飞行控制系统的稳定性方面能发挥较大作用。

1 线性调节器方程

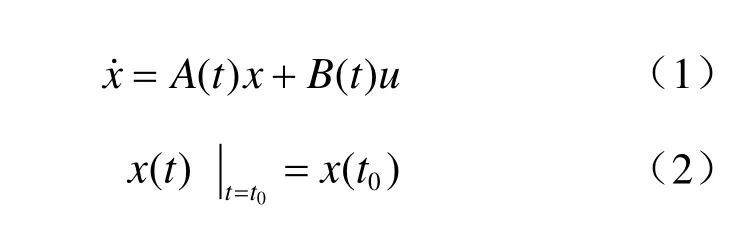
其中，x为n维状态向量；u为r维控制向量，且u不受限制。寻找一个最优控制，使

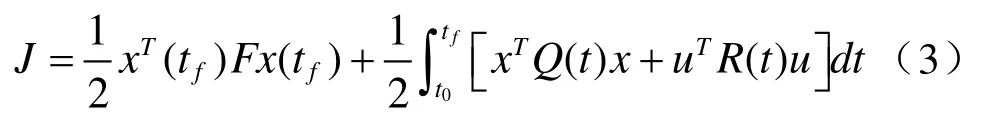
为极小。

其中，F为n∗n对称半正定常数阵；Q(t)为n∗n对称半正定时变阵。R(t)为n∗n对称正定时变阵。求解这个最优控制问题，可以用极小值原理，也可以用动态规划法。这里用极小值原理来求解。

1.1 极小值原理求解

（1）哈密顿函数为

（2）伴随方程为

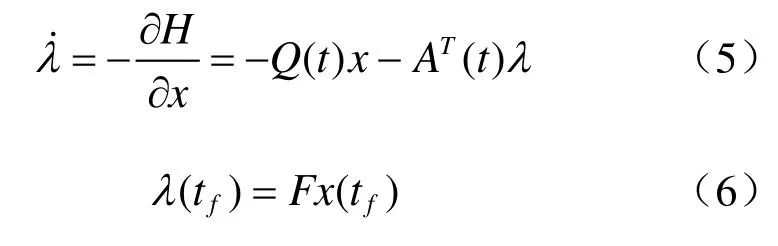
（4）将u*代入状态方程得

初始状态为x(t0)

1.2 另外一种求解方式：Riccati微分方程[1]

设

其中，P(t)为待定的n∗n时变阵。

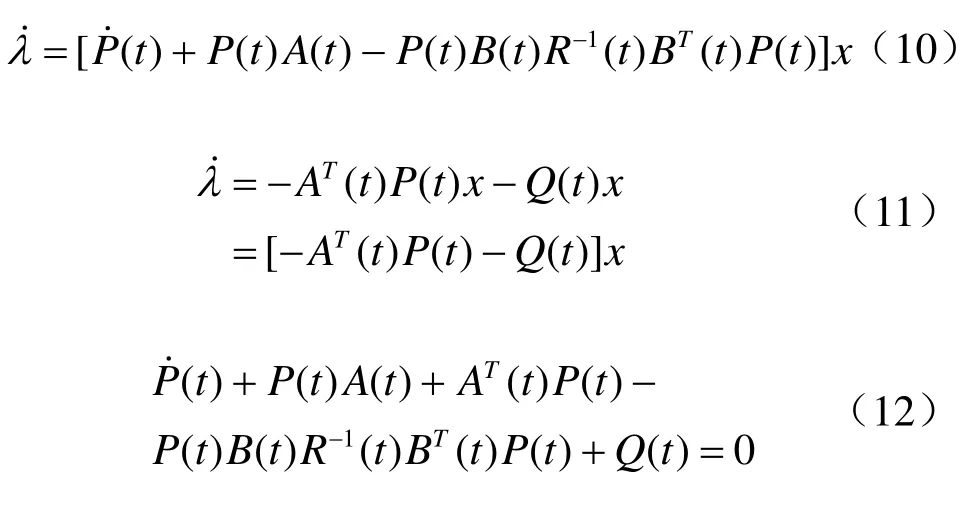
称为Riccati微分方程。其边界条件为

状态反馈的闭环方程为

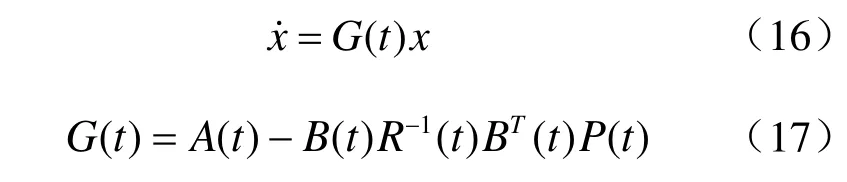
最优性能指标为

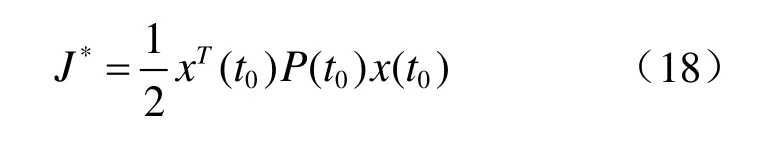
2 线性伺服机方程

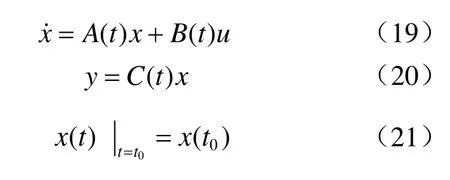
要求系统的输出跟踪指定的输入函数η(t)。η(t)与输出向量y有相同维数。寻求最优控制u*(t)，使以下性能指标取极小值[2]。

2.1 极小值原理求解

性能指标中的加权阵F和Q(t)为半正定，R(t)为正定。

控制方程为

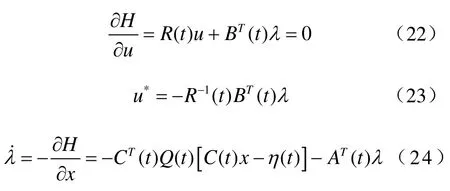
边界条件为

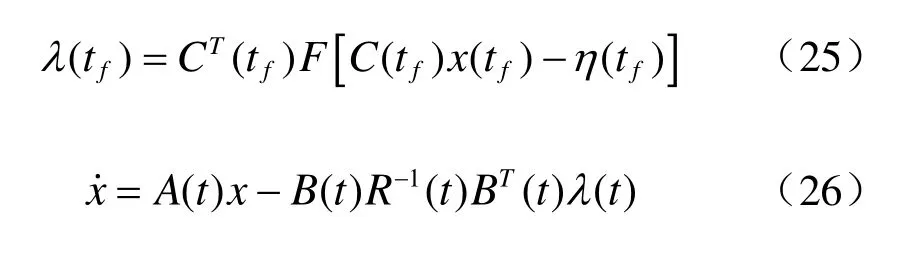
2.2 另外一种求解方式：Riccati微分方程

这时不能像线性调节器那样，仅认为λ(t)和x(t)有关系。为此，设

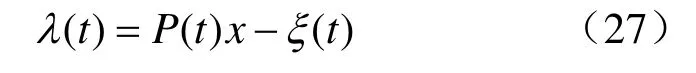
对t求导：

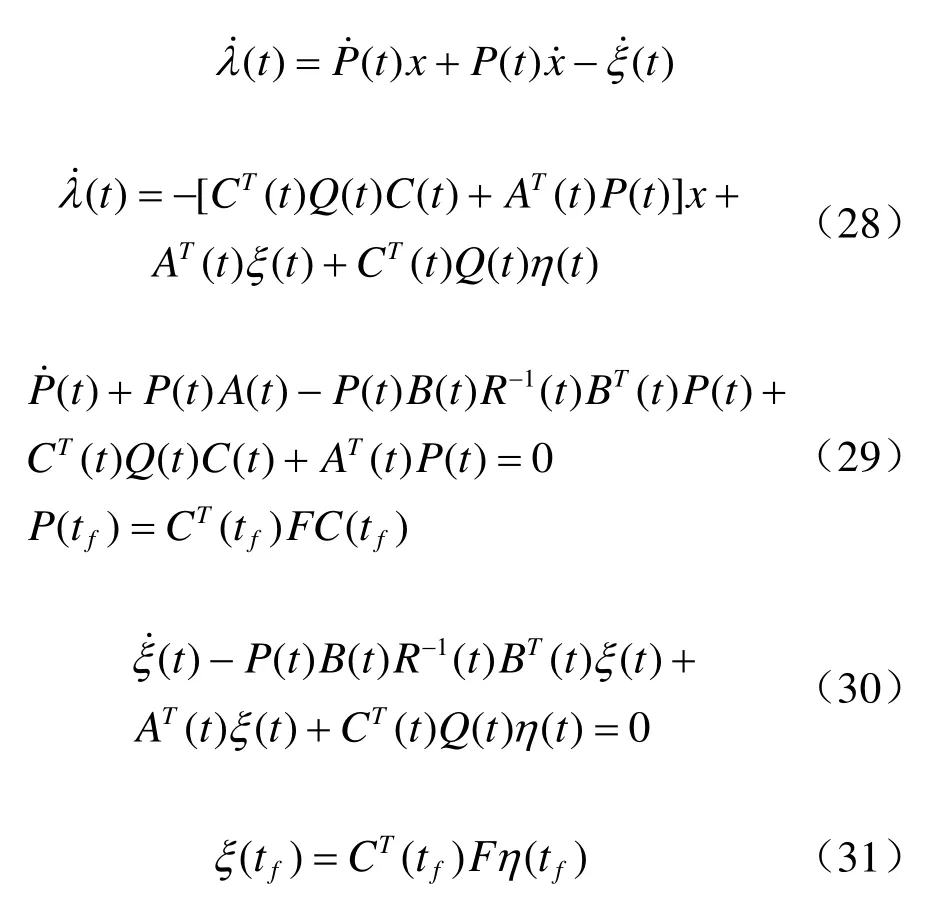
最优控制

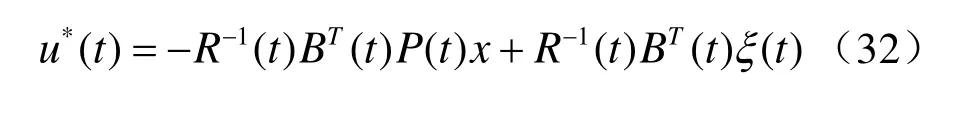
可见，u*包括两项：一项是状态x反馈；另一项代表跟踪η(t)所必须的控制信号。

线性时变系统·方程

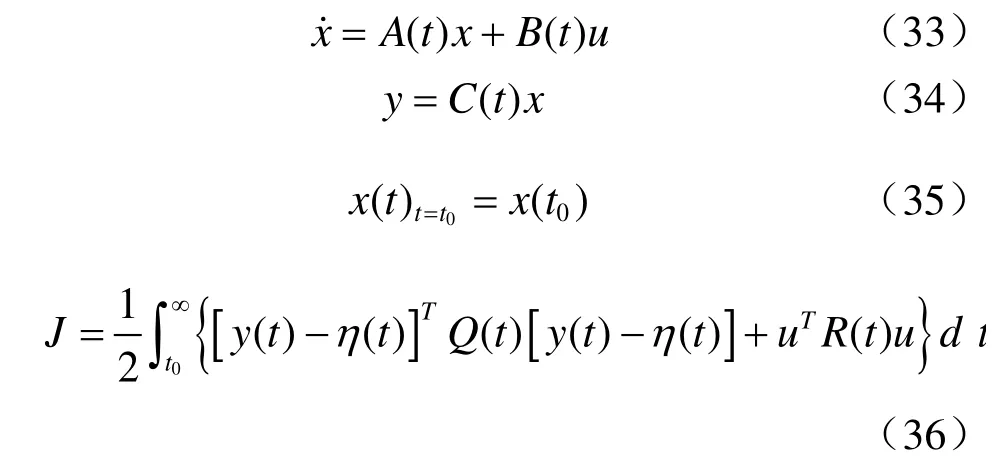
系统能控的条件下，无限时间伺服机问题的最优控制解存在，并且可以通过有限时间伺服机问题的解取tf→∞的极限求得。于是

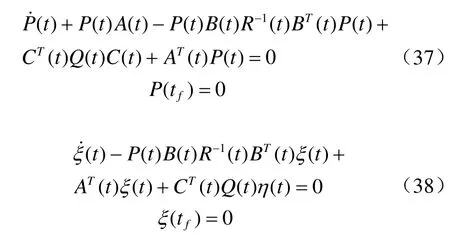
最优控制

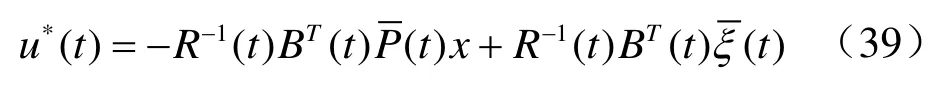
3 算法的解释[3]

系统的协态方程为

横截条件：

转移矩阵Ω(t,t0)，该齐次方程组满足初始条件λ(t)=p(t)x-ξ(t)

将Ω(t,t0)2n*2n分为四个n∗n的子矩阵，可以得到

可以得到：

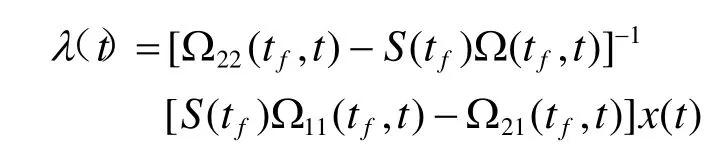
令

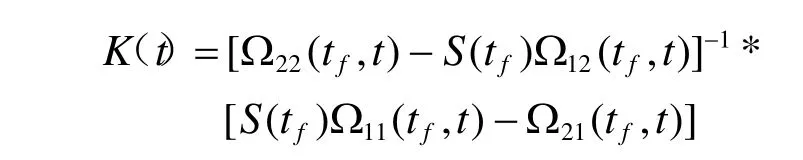
所以λ(t)=p(t)x-ξ(t)。

4 线性二次型框图

输入的控制量与反馈的状态之间会有一定误差e，通过LQR控制使得误差e保持在最小，使输出状态与预期尽可能保持一致，求出最优控制u，使误差取最小值[4]。

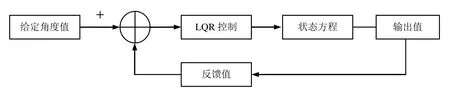
图1 LQR控制框图

5 小结

本文详细的描述线性二次型调节器的基本原理及算法，从算法的构造，推导，解算，解释等几个方面，结合线性二次型的分类，说明了该算法的详细流程。结合原理，画出了线性二次型的基本结构框图。