例谈“整合教材”进行高三数学一轮复习——基本不等式的应用

湛江市坡头区第一中学 范友玉

一、回归教材，宏观感悟——积定才有和的最小值

教师：面积不确定的矩形，能求出其周长吗？能得到其周长的最小值吗？其中面积不确定不是面积可测量而没测量，而是面积不能通过测量得到，是一个变化的值。

学生甲：面积不确定的矩形，不可能确定其周长，更不可能得到其最小值。（众生认同）

教师：结论完全正确，理由呢？

二、实践操作—限制条件的深入理解，保过三关

1.调整符号，化负为正，使之适合“一正”条件，保过第一关

学生甲：

2.拆添配凑、变动为定，使之适合“二定”条件，保过第二关

学生：没有问题，解析式类似的变形举不胜举。

教师：那你们清楚问题在哪了吗？

学生：乘积为定值的变形只有一种，最小值唯一，学生丁的解答完全正确。和或积若不为定值，我们要拆添配凑，保证定值方可验证等号是否可以取得。

3.化归转化，寻求相等，保过第三关

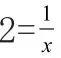
4.“三关”难过，前进受阻，应另寻出路

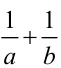
学生：这个题的解答中，ab与a+b都不是定值，却也利用基本不等式求得最值，是否与前面讲的三关有矛盾呢？

老师点评：其实从本质上讲，对于一个不等式问题，可以随意利用任何一个成立的不等式，连着用多次也没关系，但要保证不等号的方向一致，且到最后一定能放缩到一个定值，并且等号成立的条件一致，就可以取得最值。

三、结束语

本文研究的问题其实是历届学生学习过程中共有的困惑，对于学生提出的质疑，难住了不少老师。本文笔者已基本解决了基本不等式（*）应用过程中的所有困惑，实施过程中效果良好。当然还需继续实践，继续改进。