优化小学数学教材中的习题教学 提高学生解决问题能力——以切割圆柱的习题教学为例

天津市武清区石各庄镇石各庄中心小学 陈宝松

一、以习题为载体，将数学概念进行二次提升

数学概念二次提升指学生对已经掌握的知识进一步巩固提升的过程，其目的是在巩固中理解概念的本质，感悟数学思想，并将数学思想回归于解决问题，提高学生解决问题能力和创新意识值。

空间观念指由物体特征抽象几何图形，根据图形想象出相应物体，它是解决图形与几何问题的重要纽带。它是图形与几何教学的基础，是学生思维和逻辑的起点，是建立问题模型的核心。

二、数学概念二次提升的实践（人教版六年级数学下册圆柱与圆锥中练习四13题）

一根圆柱形木料底面半径0.3m，长2m，将它截成四段（如图示），这些木料的表面积比原来增加了多少平方米？

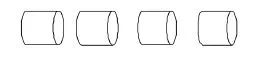
（一）化繁为简，动手操作，初步感知

让学生感受数学过程中“变”和“不变”。先让大家伸出双手攥成拳头：“两个拳头就相当于两个小圆柱。把两个拳头贴一起就成一个大圆柱，在这个过程中有什么变化？”“少两个面。”“我用刀把它切开有什么变化？”“多两个面。”我追问：“还有什么变化？”学生会说：“表面积变化。”“怎么变？”“多了。”“多什么了？”“多两个底面。” “请你和同桌把拳头贴一起，和这个题有联系吗？”学生一看便知“把大圆柱切成小圆柱。”“怎么切？”学生说：“竖着切。”“切几次？”学生可能会说“切三次、四次”“请你试试切几次？”学生自然答出：“切三次。”通过动手切，学生感受数学过程，体会分析问题思路。

（二）闭上双眼，感受过程

由动手做到闭上眼想是将学生由初步感知到数学过程的内化，是空间观念二次提升的重要环节，学生由感性认识到理性认识，学生空间观念在动和想中得到二次提升。

（三）自主探索，建构模型

引导学生探究解决切割圆柱表面积变化问题，建立起解决问题的模型。

“我们发现切割过程中，圆柱表面积增加了，你发现其中的规律吗？”这时学生会根据切割过程想到：“每切一次多了两个面。”“如果切两刀、三刀…n刀你会发现什么？”学生马上说出：“四个、六个…2n个。”

（四）拓展提高，举一反三

圆柱的切割包括横切和纵切（图示），我顺势引入另外一种切割方式。

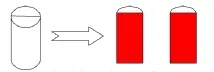
“还能怎么切？”有同学会马上说出：“沿高切或沿直径切。”我让大家闭上眼感受切割过程。“表面积有什么变化？”学生自然说出：“增加两个长方形或增加了两个切面。”“切面面积是圆柱……”学生马上说：“d×h”现在我们知道不管如何切，不论哪种物体，切完以后物体表面积之和增加的是每次切出的两个切面。

三、数学概念二次提升的教学思考

（一）激发兴趣，引发思考，探究源泉

兴趣对于学生学习的重要性不言而喻，我们要结合学生性格特点和实际去激发学生兴趣，并使之持久。学生生硬的、机械性的接受解题方法，再按图索骥的模仿是没有意义的，因为学生的思维没发展，能力没提升。兴趣是思考的源泉，促进学生思维发展，对提升学生思维能力具有积极作用。

教学中学生双手攥成拳头，就是借助学生的肢体活动激起学生学习兴趣，引导学生入题，引发学生的思考。经历圆柱切割的过程，再闭上眼想，体验圆柱切过程，思考变化规律，使问题模型水到渠成的建构。

（二）积累活动经验，感悟数学思想，体会数学价值

数学思想蕴含在知识的形成、发展和运用中，在思考、交流、推理中逐步感悟数学思想。

数学价值深植于数学思想中，它和数学知识是一体的，不可分割的。我们要善于引导学生开展数学思维的活动，循序渐进的感受数学思想是解决问题的工具，提高学生的应用和创新意识。

教学中，通过数学活动经验，再引导学生发现切割时隐藏的规律，化繁为简，合理类推，建立解决问题的模型。举一反三，想象另外一种切割，感悟两种切割的异同，总结规律，提高学生应用和创新意识。整个过程，学生借助空间观念来探究问题解决策略，学生空间观念既得到二次提升，又感悟了数学思想，体会数学价值。

一道习题在学生充分感知的基础上，动手操作，内化观念，自主探索、拓展提升，透过问题看到数学本质。空间观念二次提升中，经历操作、体验思考，感悟思想，体会价值，可见教师优化小学数学教材中的习题教学，提高学生解决问题能力的重要性不可小视。