一种博弈的异构网上行功率控制算法∗

郑创明，张海林，冯瑞

(西安电子科技大学∥综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

为了更有效地提高频谱效率，在宏基站覆盖范围内部署超密集的小小区网络 (picocells，microcells and femtocells)在第五代移动通信系统(the fifth generation，5G)中是公认的一种较好解决方案。在宏基站部署大量的发射功率和覆盖范围较小、成本较低的小小区，以增加网络覆盖和网络容量，这种网络的结构为异构网(heterogeneous network，Het Net)[1-3]。Het Net网络在给5G带来网络容量和服务质量(quality of service，QoS)提高的同时，也给它的网络资源管理和分配带来了更高的要求，同频干扰问题将成为Het Net网络中最敏感的问题[4]。基于Stackelberg的博弈论在很多文献中[5-11]已经被证明是用于通信网络资源选择与分配的可靠技术。文献[5]把博弈论与5G中的Femtocell网络的各个Femto节点的功率控制结合在一起进行研究，使得网络的整体性能最优。文献[6]利用Stackelberg博弈模型中的联合定价策略对动态频谱接入网的各个节点的功率控制进行研究，从理论上证明了通过这种方式的宏基站可以得到更高的性能增益。文献[7]通过对认知无线电网络进行研究，提出了一种基于信干噪比(signal to interference plus noise ratio，SINR)的价格函数功率控制算法，并在文中证明了这种算法的性能增益和有效性。文献[8]利用博弈论研究了双层正交频分多址(orthogonal frequency division multiple access，OFDMA)无线网络，利用价格函数解决了双层OFDMA无线网络中干扰管理与无线资源分配问题。文献[9]把博弈论应用于双层CDMA的Femtocell无线网络，提出一种基于博弈论的分布式干扰管理算法。文献[10]把博弈论应用于无线网络干扰协调算法频率复用技术中，提出基于博弈论的的频率复用算法(fractional frequency reuse，FFR)，进一步提升FFR的性能。文献[11] 利用博弈论研究了LTE-A中增强的干扰协调算法(enhanced inter-cell interference coordination，eICIC),提出了一种分布式算法，并对eICIC性能进行了优化。本文通过博弈论和异构网上行功率控制算法研究，将博弈论成功运用到异构网上行功率控制。

1 系统建模

本文研究的系统模型有一个宏基站(MBS)，在MBS覆盖范围内有K个小基站(mBS)，用集合Π表示，Π{1,…,K}；第k个mBS服务的用户数为Nk个，用集合Θk表示， Θk{1,…,Nk}；mBS服务的用户用m_UE表示，其中第k个mBS服务的用户用mk_UE表示。MBS服务的用户数为M个，用集合Ω表示， Ω{1,…,M}；MBS服务的用户用M_UE表示，其中第m个MBS服务的用户用Mm_UE表示。系统频谱资源可以分为H个物理资源块(physical resource block，PRB)，每个PRB用h∈H{1,…,H}表示。每一个用户分配的最小资源单位为PRB，由MBS服务的用户m∈Ω.对应的上行发设备功率为pm，由mBSk∈Π服务的用户n∈Θk对应的上行发设备功率为定义所有与用户n使用同一PRB的用户的集合为Sn。模型中用户n与其服务的基站k传输对之间的信道增益用gn,k表示。σ2为加性高斯白噪声的方差，该值可认为是不变的。第k个mBS服务的用户n检测到的上行信干噪比γn,k如公式(1)。

(1)

其中,In=gm,kpm+∑j∈Sn,j≠ngj,kpj为用户n受到的上行干扰。同理, 由MBS服务的用户m∈Ω的上行信干噪比用γm表示，与用户m使用相同PRB且由mBS服务的用户集合为Sm，因此γm的计算方法如公式(2)，gm,M表示用户n与MBS之间的信道增益。

(2)

(3)

2 异构网中博弈的上行功率控制优化

把用户n的效用函数定义为其信息传输速率Cn,k。借鉴文献[7]中定义价格为γn,k的二次型，本文采用pn的二次型作为价格cn，如公式(4)。

(4)

λM和λm是由MBS确定的定价因子。MBS对用户造成的干扰作出定价，一方面可以补偿自己的速率损失，另一方面用来惩罚那些干扰其他用户的用户。按这种思路，用户的支付函数μn定义为效用与价格的差，如公式(5)。

μn=Cn,k-cn=

(5)

2.1 mBS的上行功率控制优化

mBS服务的用户n的功率控制问题转化为下列问题的优化。

(6)

通过对支付函数进行一阶与二阶求导[12]，可以得到公式(7)-(8)。

(7)

(8)

使式(7)等于0，经过整理得到式(9)：

(9)

式(9)是一般一元二次方程，有两个实数解，选择其中的正值，利用求根公式得到式(10):

(10)

进一步，从公式(8)可以得到：

(11)

(12)

2.2 MBS的上行功率控制优化

为简化计算，由于本文中的MBS为单个扇区，没有配置其它的MBS邻区，因此MBS对其服务用户的m功率控制可以采用公式(13)进行计算。

(13)

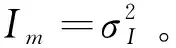
pm= 0.5×

(14)

之后根据约束条件，由公式(12)最终确定用户的发射功率。

3 基于博弈论的用户上行功率控制算法

在移动通信网络中，上行功率控制属于无线资源管理的一部分。产品中的无线资源管理是由调度器完成，它在每个传输时间间隔(transmission time Interval, TTI)利用调度算法完成各个用户的资源分配，其中包括频谱资源、时间资源和功率资源。本文重点研究用户的上行功率资源分配，即上行功率控制。从公式(14)中可以看出，M_UE的上行发送的最优功率不包含m_UE的发射功率参数，因此首先利用M_UE用户之间的发射功率博弈过程确定M_UE的最优上行发射功率。其次把求出的M_UE最优上行发射功率代入公式(10)，再利用m_UE用户之间的发射功率博弈过程，求得m_UE的最优发射功率。

3.1 MBS的上行功率控制算法

MBS的上行功率控制算法步骤如下：

1)MBS首先根据调度算法，对选定本次待调度的M_UE进行调度优先级排序，其中优先级最高的排在队首，该队列用QM表示。

2) MBS对队列用QM的用户按照优先级由高到低的顺序对M_UE进行资源初次分配，包括为每个M_UE分配PRB，频谱效率或调制解调方式和上行发射功率，通过初次资源分配得到本次调度的M_UE集合Ωs，其中Ωs⊆Ω。

6)上行功率控制博弈结束，根据得到的功率分配结果，按照最优的功率进行资源重新分配。

7)把最优的M_UE上行发射功率结果发送给mBS，用于mBS的上行功率优化。

3.2 mBS的上行功率控制算法

在对M_UE的上行功率优化后，mBS采用公式(10)对m_UE进行功率优化，公式中的同频干扰In计算中包含M_UE的功率。因此，mBS对m_UE进行功率优化之前需要获得M_UE的功率。具体步骤如下：

1)获得优化后的M_UE上行发射功率。

2) mBS首先根据调度算法，对选定本次待调度的m_UE进行调度优先级排序，其中优先级最高的排在队首，该队列用Qm表示。

3) 对队列用Qm的用户按照优先级由高到低的顺序对m_UE进行资源分配，得到本次调度的m_UE集合Өs，其中Өs⊆Ω。

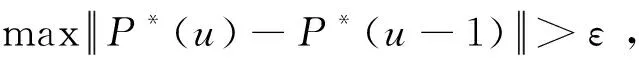
7)上行功率控制博弈结束，mBS利用最优的m_UE功率进行资源重新分配。

4 性能仿真分析

4.1 仿真参数设置

系统仿真的网络设置为1个MBS小区，MBS天线采用全向天线，覆盖半径为500 m，在MBS的边缘区域布置12个全向天线mBS，每个mBS的覆盖半径为165 m，如图1。MBS和mBS全部采用LTE技术，且空口采用同频组网。上行小区用户分布采用随机撒点的方式，系统的网络拓扑结构布局如图1所示，图中的三角形符号为BS，系统仿真平台采用OPNET 14.0。本仿真配置的用户数和覆盖的面积成正比，M_UE与m_UE的比例为7∶12，定价因子λM和λm配置为1，仿真中运用的主要仿真参数为如表1。

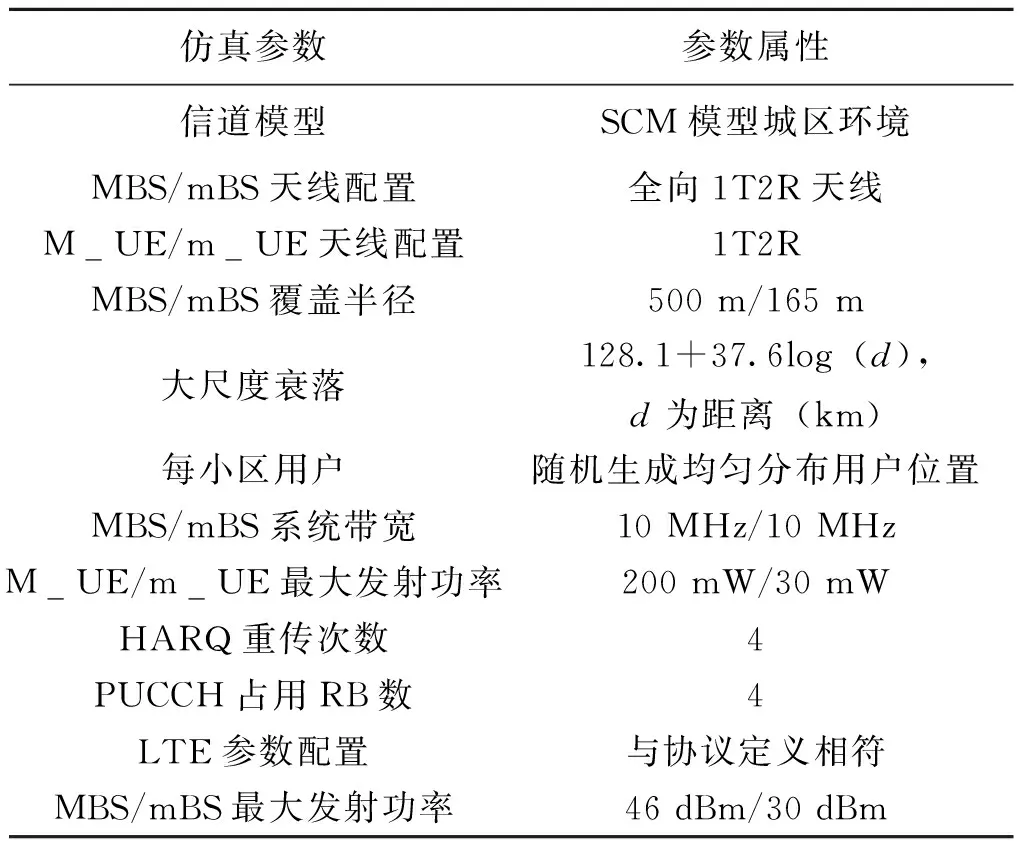
表1 仿真参数Table 1 Simulation parameters

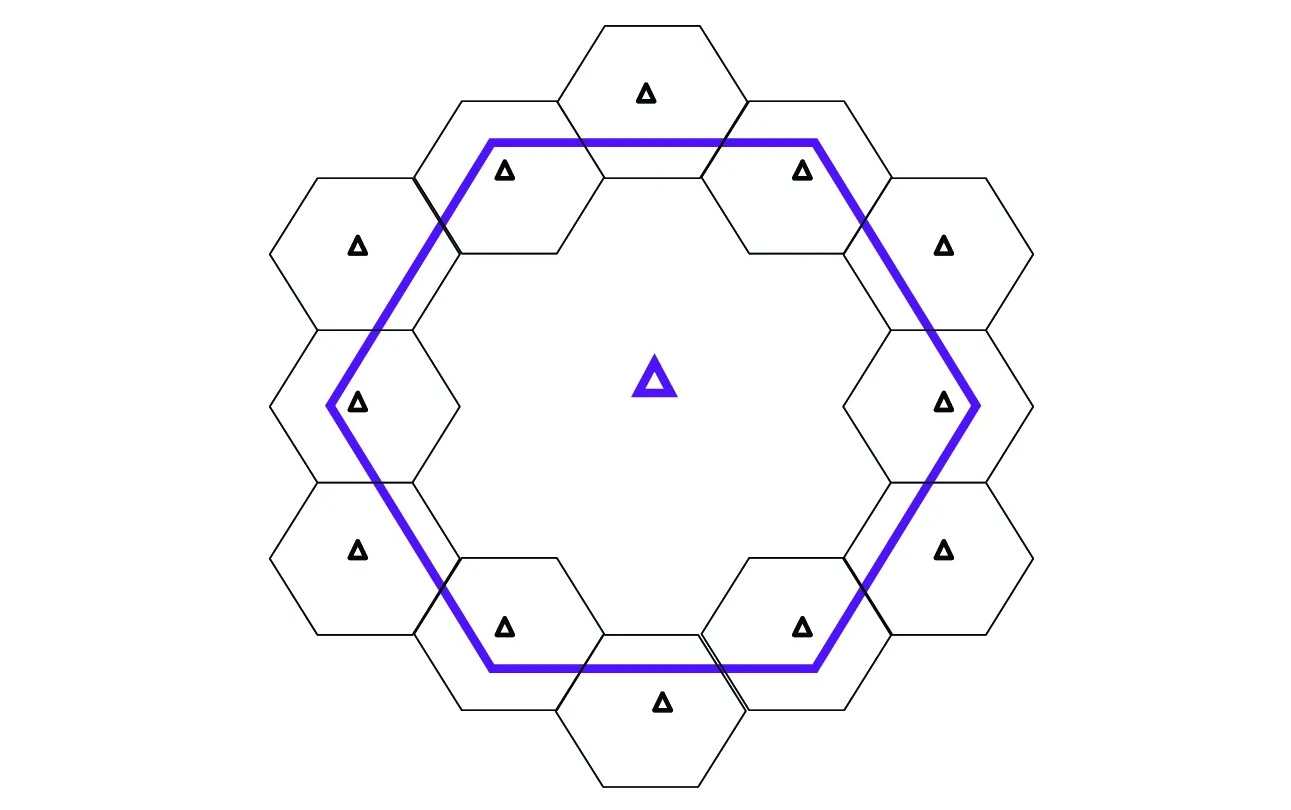
图1 仿真的网络拓扑结构Fig.1 Network topology for simulation

4.2 业务模型配置和LTE上行功率控制

本文仿真采用的业务模型为LTE协议定义的non-GBR,用户的QCI等级为9，M_UE/m_UE平均每个用户的数据速率为 0.8 Mbps/4 Mbps。分别对网络内的用户数为38 UEs，57 UEs，76 UEs，95 UEs，114 UEs，133 UEs时的系统性能进行仿真。为便于证明本文提出的算法的性能，采用与LTE协议定义的上行功率控制进行性能对比。LTE的上行功率控制过程为：首先基站根据UE上报的自身检测到的下行信道质量，估算对应UE的上行链路增益，然后综合考虑用户UE的功率余量确定对应用户UE的上行接收信干燥比大小，然后转化为频谱效率，并通过上行授权的方式发送给对应的UE，UE利用上行授权和当前的功率信息从而计算自己的上行发射功率，并通过上行闭环功率控制的方式进行动态调整每次的UE发射功率，本文闭环功率控制调整步长为1 dB，闭环功率控制命令由对应的基站通过对应的信道发送给对应的UE。

4.3 算法的系统性能仿真与评估

图2为基于博弈的上行功率分配算法和现有LTE功率控制算法的系统上行吞吐量性能曲线。从图2中可以看出，两种功率控制算法在网络负载较轻的场景(系统UEs的数量不大于57 UEs)下的吞吐量性能基本相同；随着用户数量的增加，基于博弈的功率分配算法性能优于LTE的功率控制算法，并且在网络用户为95 UEs达到系统最大吞吐量；之后，随着用户数量的增加，系统的吞吐量会出现轻微的下降，主要原因是当用户数量增加时，需要的上行业务量也随之增加，系统资源被充分利用，干扰分布变得更为复杂，这就给功率控制带来了更多的不确定性，因而导致系统吞吐量下降。由于博弈的上行功率分配算法实际上是在原来的功率控制的基础上进行了用户功率分配的二次优化，优化考虑了对其它同频小区用户的干扰，因此带来了性能增益。

图2 系统上行吞吐量性能Fig.2 System uplink throughput performance

图3为基于博弈的上行功率分配算法和现有LTE功率控制算法的系统能效比性能曲线。从图3可以看出，基于博弈的上行功率分配算法在网络业务部分加载、全部加载场景中都能得到更高的能效比，更能体现基于博弈的上行功率控制算法的性能优势。在网络业务部分加载场景，由于各个小区的资源存在部分空闲，干扰水平较低，用户的发射功率就会降低，因此获得更高的能效比；当网络业务全部加载时，系统资源被充分利用，干扰变得较大，因此能效比下降。

图3 能效比性能Fig.3 Energy efficiency ratio performance

图4为基于博弈的上行功率分配算法和现有LTE功率控制算法的HARQ重传次数的CDF性能。从图4中可以看到，在95 UEs时，基于博弈的上行功率分配算法的HARQ重传次数明显减少，业务分组大部分都能在一次传输就完成，需要重传的机会明显小于现有LTE功率控制算法。这充分说明，基于博弈的上行功率分配算法由于采取博弈论的方法对上行功率进行优化，使得UE的上行功率分配更加合理，更符合实际的场景需求。

图4 HARQ重传次数CDFFig.4 HARQ retransmission CDF

5 结 论

本文通过对博弈论和上行功率控制算法的研究，提出一种博弈的异构网上行功率控制算法。在本文中给出了系统模型的建立方法，以及最优功率的理论和计算。通过与现有的LTE调度算法的对比，验证了该算法的性能优势。在研究过程中也遇到很多新的问题，因异构网络的资源管理中涉及许多技术，如果把基于博弈的异构网上行功率控制算法和异构网络中的频率规划或软频率复用、移动性管理相结合，将会得到更大的系统增益。