单台风电机组尾流流场模拟
李品,王东升,崔岩松
(1.河北建投新能源有限公司,河北 石家庄,050000;2.东方电气自动控制工程有限公司,四川 德阳,618000)
0 引言
在风电场中,风经过旋转的风轮后会发生速度大小和方向的变化,这种对初始空气来流的影响称之为风力机的尾流效应。尾流导致气流中附加风剪切和湍流强度,这会影响下游风力发电机组的疲劳载荷和结构性能等因素,减少风力机的输出功率,进而影响整个风电场的总输出功率。因此,开展风电机组尾流场的研究对于合理布置风力发电机组,减少风力发电机组间尾流干扰,进而提高整个风电场的发电效率有着重要意义。
国内外许多专家学者对风电机组的尾流效应开展了广泛研究,一类是尾流模型研究方法,这些模型是由学者提出的简化尾流模型,然后利用实验数据检验模型并且进行修正。比如WAsP采用的Park模型、Ainslie提出的涡粘性尾流模型、Larsen尾流模型、 Jensen模型、 AV(Aero
Viroment)尾流模型等等。其中Larsen模型是基于旋转对称湍流边界层公式的渐进表达式的半解析尾流模型,尾流区边界非线性并且某一点的风速除了与风力机后距离有关还与距离中线的距离有关,更加符合实际,在欧洲风电机组项目标准中被推荐使用。还有一类是基于CFD的数值模拟,CFD方法应用计算机数值计算和图形显示两种手段,将计算域分成时间和空间进行描述进而求得数值解。CFD采用了反应粘性流动的不可压缩流体N-S方程,并不像尾流模型对实际情况进行过多的简化,比较准确地模拟了流场情况。南京航空航天大学的王同光、钟伟结合致动盘理论和CFD方法对尾流边界问题进行建模和研究。结合致动盘的CFD方法,把风力机简化为一个无限薄的制动盘,通过设置制动盘前后的压差来计算风力机后速度的分布。这种方法虽然简单但是没有考虑到风力机旋转对尾流区风速分布的影响,因此该文采取了建立风力发电机整机模型模拟风轮旋转的方法来计算得到尾流区域风速分布情况,更加符合实际。
该文主要研究内容是采用基于CFD的数值模拟方法来研究尾流流场,进行了单台风电机组三维流场建模、模拟仿真计算以及实验结果分析。用Larsen尾流模型进行尾流区风速分布的计算,并与Fluent数值模拟结果相互对比。
1 计算模型的建立与数值模拟
1.1 风力发电机组与流场的几何建模与网格划分
风力发电机组叶片采用的是NREL Phase VI S809翼型,该数据取自美国可再生能源实验室(NREL)的一篇技术报告。最终建成如图1的整机模型,重要参数为风轮直径10 m,叶片数为3,塔筒高度12 m。

图1 风力发电机整机模型
流场即为流体运动的区域,在风力发电机组外建立一个5D×5D×28D的长方体作为流场,如图2(a)所示,风力发电机组前后的流场划分为3D和25D。网格的生成其实就是流场的离散,网格质量和数量对计算精度和计算时间都有很大影响。网格分为结构性网格和非结构性网格,划分网格的原则是能生成结构性网格就尽量先生成结构性网格。为了提高网格质量,只在风力发电机附近采用非结构性网格,其余部分采用结构性网格,对流场进行了分块。通过调节线网格疏密程度的变化,使得接近风机的网格比较密集,远处比较稀疏,在保证精确度的前提下减少网格数量。最终得到图2(b)的网格划分。
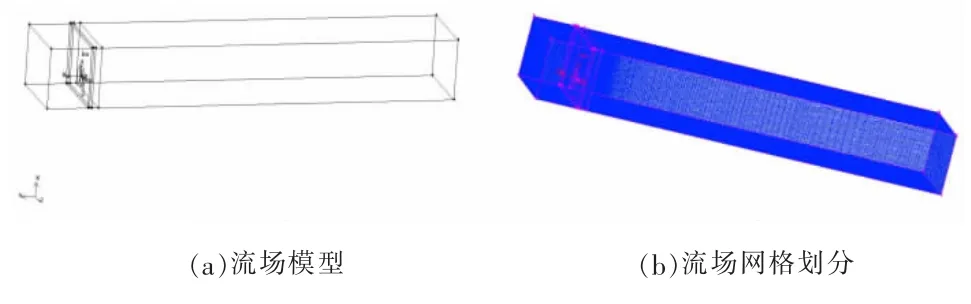
图2 流场建模与网格划分
1.2 模型的求解与边界条件的设定
Fluent采用的是有限体积法,先将计算域划分为网格,并使每个网格节点周围有不重叠的控制体积,然后将等待求解的微分方程对每个控制体积积分,从而可以得到一组离散方程,最后通过求解方程组得到要求解的各个物理量。计算流体力学的问题大部分是要求解每个时间点对应的流场物理量,实际上是求空间网格上的压力、速度、温度等物理量。有限体积法是把非线性偏微分方程变成网格上的线性代数方程,然后求解这些线性代数方程从而得到流场的解。基于压力的分离求解器主要应用于不可压缩流动,隐式求解思路是同时求解方程,比显式求解收敛速度快,但计算量大。
入口边界设置为速度入口,定义恒定速度12 m/s,不考虑风剪切的影响;由于出口足够远,认为已经恢复大气压,出口边界设置为压力出口壁面边界;流场外轮廓面和塔筒机舱面全部定义为静止壁面,风轮表面定义为移动壁面;划分流场区域时产生的表面定义为内部表面。选择基于压力的分离隐式求解器,对连续方程、动量方程、能量方程、湍流方程进行耦合求解。通过设置风轮区域的坐标系为旋转坐标系,叶片表面相对于旋转坐标系同步旋转的移动壁面来实现对风轮旋转的模拟。
2 尾流流场特性
从计算得出的图3风速分布图可以看出风速在风力发电机组后方有明显降低,之后再慢慢恢复至来流风速,随着尾流向下游发展,亏损逐渐减小,尾迹宽度逐渐增大。风轮和塔筒附近的速度等值线梯度大说明风速减小的速率很快,但是速度恢复的等值线就没有如此密集了,变化较为缓慢,由于忽略了风剪切的影响所以总体看来风速分布呈中心对称分布。

图3 风轮中心高度水平面风速等值云图
靠近风力发电机后的区域内两侧出现明显的高速区,这是由于在近尾流区叶尖涡的影响比较明显造成的,叶尖切向速度非常大,云图反应的是合速度的大小,因而在两侧出现高速区。叶尖涡的存在是尾流区域结构的一个重要组成部分,在远尾流区叶尖涡以近似线性的规律向外延伸,与叶根涡共同组成螺旋形涡系。但是在远尾流区叶尖涡的影响已经很小了。叶尖涡是由于风轮旋转造成的,这在尾流模型的计算方法和结合致动盘的CFD方法中是无法体现的。
3 计算结果分析
3.1 Fluent计算结果分析
从图4风轮后不同轴向距离处速度沿径向分布图,也可定量地看出风经过风轮后速度逐渐增大和由中轴线向两侧逐渐增大的趋势。由图5可知,叶尖速比是尾流区域风速分布的一个重要影响因素,叶尖速比越大即风轮转速越快则尾流效应越明显,风轮后风速衰减越厉害。风轮旋转会引起风力机下游产生较强湍流和尾涡,尾涡向下游发展扩散进一步消耗空气中的能量,导致风速降低,转速越快效果越明显。风洞实验的结果也包括了风轮旋转造成的风速损失,这也是利用尾流模型计算和致动盘方法所不能体现的。
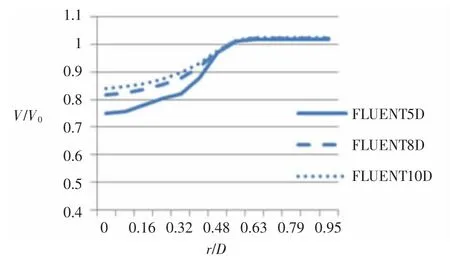
图4 风轮后不同轴向距离处速度沿径向分布图
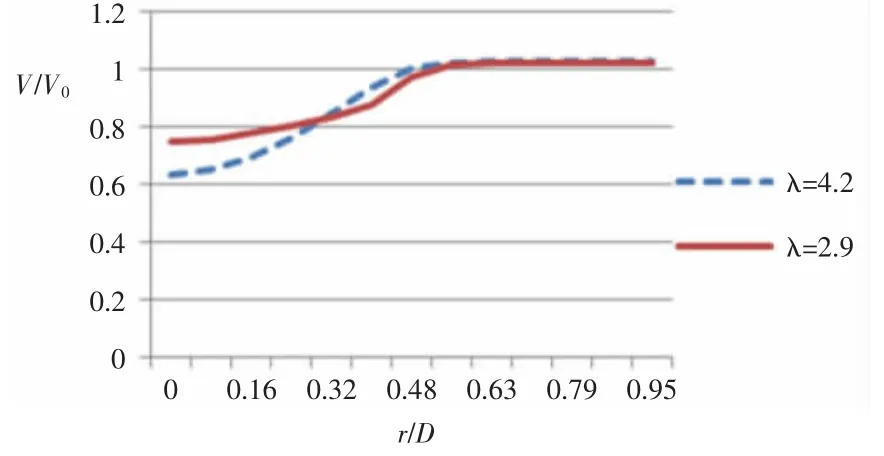
图5 不同λ时风轮后5D处风速沿径向分布图
3.2 Fluent计算结果与Larsen模型计算结果对比
3.2.1 Larsen尾流模型
Larsen模型是基于Prandtl旋转对称湍流边界层公式的渐进表达式的半解析尾流模型。它假设空气流动为不可压缩稳态流动,并且忽略了风切变的影响,因此尾流区是轴对称的。由于Larsen模型更加接近实际,所以在欧洲风电机组项目标准中被推荐使用。 Larsen模型的计算公式如下,风力发电机组后风速衰减的大小与轴向推力系数Ct、距离风轮的轴向距离x以及距离中轴线的径向距离r有关。

3.2.2 风轮中轴线风速大小对比
从Fluent计算结果中,读取中轴线上的风速数据以及风轮所受推力,然后根据公式计算得到轴向推力系数Ct,带入Larsen模型计算公式就能得到Larsen模型计算公式的其他参数c1和x0。通过matlab对公式进行编程,由于中轴线上r=0,所以只需带入纵坐标就能够得到各位置速度大小,两者结果对比如图6所示。从图中可以看出,近尾流区风速变化梯度较大,远尾流区较小。
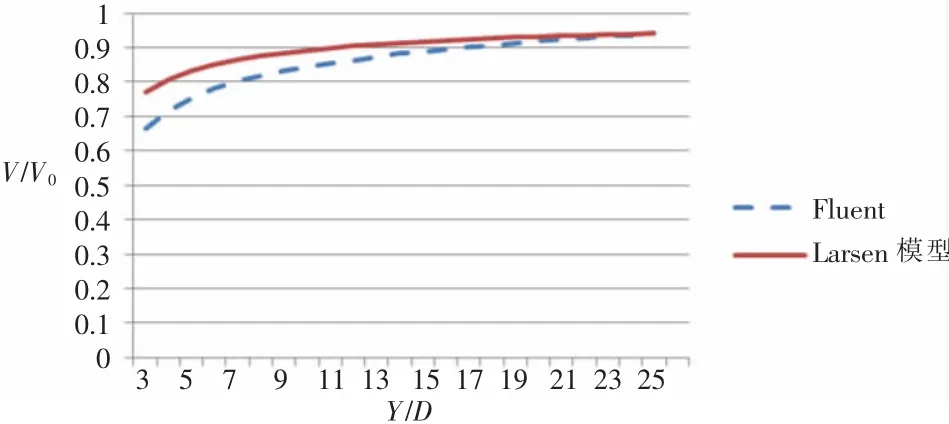
图6 风轮中轴线风速大小对比
3.2.3 风轮后不同位置处尾流区直径上速度对比
从Fluent仿真计算结果中分别在风轮后3、5、8、10、13、15倍风轮直径距离处取直径线上的点及其速度值。再将这些点坐标带入Larsen模型计算公式,计算得到对应的速度值。最后通过数据处理,即可对二者进行对比生成鲜明的折线对比图,如图7所示。由于直径上速度数据是关于原点对称的,所以只比较了直径上一半的数据。

图7 λ=2.9时风轮后不同位置处速度对比

图8 λ=4.2时风轮后不同位置处速度对比
图7和图8给出了不同叶尖速比下风力机下游不同位置叶轮中心高度处风速分布,显示了Fluent与Larsen模型计算结果的对比,二者计算结果比较接近,但Fluent计算结果尾流区半径比Larsen尾流模型计算结果要小,二者在尾流区域半径大小上也存在一定误差。
4 结论
采用基于CFD的数值模拟的方法来研究尾流流场,对单台风力发电机后的整个流场进行数值模拟,研究远尾流区中风速的分布规律,并与Larsen尾流模型计算结果进行对比验证,得到如下结论:
(1)当来流吹过风力发电机,风速先急剧下降后缓慢恢复,尾流区域逐渐扩张,并且风轮转速越大,尾流效应越明显。
(2)通过进行Fluent仿真结果与Larsen尾流模型的计算结果对比,包括中心轴上速度大小的对比和风轮后不同位置处直径线上速度大小的对比,表明该方法可用来研究尾流区域风速分布,可为风电场微观选址提供一定参考。Larsen模型计算方法由于没有考虑风轮旋转对尾流区风速分布的影响,在近尾流区计算结果与Fluent模型计算结果有较大偏差,在远尾流区二者结果比较接近。

