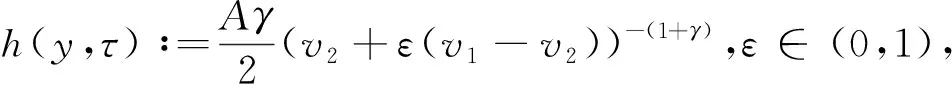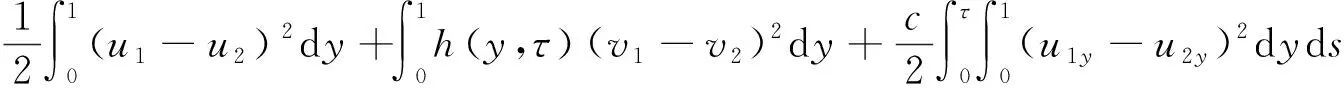带有真空的可压缩向列型液晶系统整体弱解的唯一性

孔春香

(延安大学 数学与计算机科学学院，陕西 延安 716000)

1 引 言

本文考虑拉格朗日坐标下一维可压缩向列型液晶系统[1-3]的初边值问题：

(1)

其中(ρ,u,n):[0,1]×[0,)→R+×R×S2, 分别代表流体密度、流体速度场以及液晶分子的单位方向向量场.压力函数P(ρ)=Aργ(A>0,γ>0),μ、λ、θ为正的物理参数.为便于计算，取μ=λ=θ=1. 系统初始值和边界条件满足：

(ρ,u,n)t=0=(ρ0,u0,n0)(y),∀y∈[0,1]

(2)

ρ(0,τ)=ρ(1,τ)=0

(3)

有关液晶流体系统问题，相关学者做了一些研究;当小密度函数有正的下界时，文献[4]考虑了在不同边界条件下一维液晶流体系统整体解和强解的存在性和唯一性以及弱解的存在性.文献[5]获得了整体对称强解的存在性.文献[6]研究了三维欧氏空间有界区域中向列型液晶流体的一个耦合的非抛物耗散动力系统的全局弱解的存在性.

假设初始值满足下列条件：

(A2)u0,(ρ0u0y)y∈L2([0,1])

定义1 函数ρy,τ、uy,τ、n(y,τ)为初边值问题(1)-(3)的一个整体弱解，若对任意的T>0,有

ρ,u,n∈L0,T∩C0,T,L2(0,1)

ρny∈L0,T∩C0,T,L2(0,1)

ρuy,ρ(ρny)y∈L

进一步方程(1)是成立的，对几乎所有的y∈0,1和∀τ≥0,并且

2 先验估计和唯一性的证明

引理1[2]0

‖u‖L([0,1]×[0,T])+‖ρ(ρny)y‖L([0,1]×[0,T])≤c

本文中‖•‖表示L2范数，c表示通用常数，不同的地方代表不同的常数.

定理1 在条件(A1)、(A2)、A3下，令ρ1,u1,n1(y,τ)、ρ2,u2，n2(y,τ)为初始边界值问题(1)-(3)在0≤τ≤T的两个解，并满足正则性条件，则对于几乎处处的(y,τ)∈[0,1]×[0,T],有

ρ1,u1,n1(y,τ)=ρ2,u2,n2(y,τ)

证明:设(ρ1,u1,n1)、(ρ2,u2,n2)都是方程的解，并设

首先由(1)知(ρ1,u1)和(ρ2,u2)满足∂yui=∂τvi,i=1,2

(4)

由(2)和 (4)式，可得

(5)

方程(5)两边乘以u1-u2在[0,1]上积分，并分部积分，利用边界条件(3)和(4)式、引理1、Lagrange中值定理、Young不等式及嵌入定理得到

即

(6)

hτ(y,τ)≤c1(v2τ+v1τ-v2τ)

(7)

(8)

将(8)代入 (6) ，其结果在(0,τ)积分，利用已知条件得到

由于h(y,τ)≥c>0，所以有

(9)

利用嵌入定理 得

对(9)式利用Gronwall不等式，可得

即ρ1(y,τ)=ρ2(y,τ),u1(y,τ)=u2(y,τ).

由(1)的第3式，有

(10)

J1+J2+J3+J4+J5+J6+J7+J8

(11)

利用引理1和Young不等式得

则有

(12)

由Gronwall不等式和引理1，得

即n1(y,τ)=n2(y,τ).定理得证.