粘性Cahn-Hilliard方程的指数吸引子
曹伯芳, 姜金平, 曹兰兰
(延安大学 数学与计算机科学学院,陕西 延安 716000)
Cahn-Hilliard方程用以描述物理、化学中的二体相变问题,关于Cahn-Hilliard方程已有大量的研究,文献[1]证明了黏性Cahn-Hilliard方程弱解的唯一性,文献[2]证明了粘性Cahn-Hilliard方程在H1中的弱解的存在性.文献[3-6]讨论了Cahn-Hilliard方程的相关吸引子的存在性.本文在文献[3]的基础上,进一步研究以下粘性Cahn-Hilliard方程的指数吸引子的存在性:
ut+Δ2u-δΔut=Δfu,x,t∈Ω×0,
u=Δu=0,x,t∈∂Ω×0,
(1)
ux,τ=uτx,t>τ0
其中Ω⊂Rnn≤3是具有光滑边界的有界区域,这里δ>0是粘性系数,fu是首项系数为正的奇次多项式:
(2)
并且存在正的常数C1,C2,l满足:
fuu≥-C1
(3)
fu≤C21+up
(4)
f′u≥-l
(5)
1 预备知识

定义1[7]半群St在B中是Lipschtz连续的,如果存在不依赖于u,v的局部有界函数φt,使得
‖Stu-Stv‖Ω≤φt‖u-v‖Ω,∀u,v∈B⊂V
(6)
成立
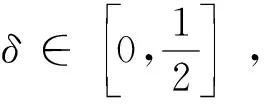
‖Stu-Stv‖≤δ‖u-v‖
(7)
或者有
‖QMStu-Stv‖≤‖PMStu-Stv‖
(8)
成立.
引理1[8]如果半群St:V→V存在吸收集B⊂V及紧的全局吸引子A,并且半群St在B中具有Lipschitz连续性和挤压性,则半群在V中存在指数吸引子.
2 指数吸引子的存在性
由文献[3]可知,问题(1)对应的解半群S(t)在V中存在有界吸收集B和全局吸引子A,故由引理1,只需证明S(t)满足Lipschitz连续性和挤压性即可得指数吸引子的存在性.
引理2 设f满足(2)~(5)式,ut和vt是问题(1)的两个解,初值分别为u0和v0∈B,则
‖ut-vt‖≤e2d0t‖u0-v0‖
(9)
即解半群S(t)在B中具有Lipschitz连续性.
证明: 令wt=ut-vt,则由(1)可得
wt+Δ2w-δΔwt=Δfu-fv
(10)
w作用于上式两端有
(11)
又因为
(12)
将(12)式代入(11)式,得
(13)
(14)

(15)
利用Gronwall引理,得
‖wt‖2≤e2d0t‖w0‖2
(16)
引理3 设f满足条件(2)~(5),ut和vt是问题(1)的两个解,初值分别为u0和v0∈B,则解半群St在B中具有挤压性.
证明: 记A=-Δ,设A在V中的特征值为λii=1,2,···,满足0<λ1<λ2≤λ3≤···,λi→(i→).用wi表示特征值λi对应的特征向量,则wi构成V中的一组标准正交基,同时也是H中的一组正交基,并且满足Awi=λiwi,记
HM=spanw1,w2,···,wM
对任意的w∈V有如下的正交分解:
(17)
其中PM:V→VM是正交投影
将试验函数q作用于(10)式,得
(18)
因为
l‖w‖‖
(19)
(20)

(21)
对(21)式使用Gronwall引理,有
‖q‖2+δ‖
若‖QMwt‖≤‖PMwt‖,则挤压性自然成立,故只需验证‖QMwt*‖≥‖PMwt*‖t*>0.
假设‖QMwt*‖≥‖PMwt*‖t*>0.利用(17)式,有
‖wt*‖2=‖PMwt*‖2+‖QMwt*‖2≤2‖QMwt*‖2
因此

即
挤压性得证.
由引理2和引理3,可得如下结果.
定理设f满足(2)~(5),则解半群St在V中存在指数吸引子.

