Carleman类模型光滑解的整体存在及渐近分析
陆小菲, 林春进
(河海大学 理学院,江苏 南京 211100)
1 引 言
本文中Carleman类模型为:
(1)
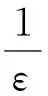
考虑Carleman类方程(1)的宏观量为粒子的质量和动量,分别定义为:
利用宏观变量ρε和jε,方程(1)改写为如下关于宏观质量及动量的方程组:
(2)
和初值条件
(3)

方程组(2)是一个带部分耗散的对称双曲方程组,其光滑解的存在性研究可以追溯到20世纪70年代[5-8].文献[9-11]讨论了含有ε的方程组的松弛极限,利用解关于ε的一致先验估计,获得解的渐近行为。本文借鉴文献[9-11]中的部分技巧,但没有使用Kawashima条件[12],直接从方程组出发获得解关于ε的一致先验估计,进而得到光滑解的整体存在性,即:

其中c不依赖于ε.
在定理1的基础上,我们对解进行渐近分析.利用关于ε的一致先验估计,可以获得解收敛于非线性扩散方程的解,并且解以速度ε收敛,即本文的第二个结论:
定理2 假设定理1的条件满足,记(ρε,jε)是定理1中初值问题(2)(3)的唯一光滑解,设r(t,x)∈C(+;Hk()是如下初值问题
(4)
的唯一光滑解.则对于任意的0 其中c(T)只依赖于T,不依赖于ε. 对方程(2)进行变量替换t=ετ,令: 忽略 中的ε、~,方程组可以写成如下形式: (5) 和初值条件: ρ(0,x),j(0,x)=ρ0(x),j0(x)=u0+v0,u0-v0 令 由Sobolev嵌入定理,有下面不等式成立: 其中c为常数. 为了获得方程(5)光滑解的整体存在性,首先证明解的先验估计. 证明注意到 利用ρ的一致有界性,ραj2的积分可以被j的L2([0,T]×)范数控制,于是有: (6) 对(5)两边关于x求偏导,将第一个式子两边同乘ρx,第二个式子两边同乘jx,并在[0,T]×上积分,再将两式相加: 则有: (7) 然后对(5)的第二个式子两边同乘ερx,并在[0,T]×上积分,得: (8) 利用Cauchy-Schwarz不等式和分部积分,两个积分分别估计为: 将上面估计代入(8),利用不等式(7),可得ρx的L2([0,T]×)估计: (9) 综合(7)、(9),得到关于ρx,jx的估计: (10) 对(5)两边关于x求二阶偏导数,将第一个式子两边同乘ρxx,第二个式子两边同乘jxx,并在[0,T]×上积分,再将两式相加.过程与前面类似,得到: (11) 对(5)的第二个式子两边关于x求偏导,并同乘ερxx,再在[0,T]×上积分: 类似前面的估计,对右端三项进行估计,得到关于ρxx的估计: (12) 综合(11)(12),得到ρxx,jxx的估计: (13) 综合(6)、(10)、(13),引理1证明完毕. 证明利用引理1的结论,假设存在常数c0≥1,使得若ρ(τ,x),j(τ,x)∈C([0,T];Hk())是(5)的解,且满足Nε(T)≤1,则ρ(τ,x),j(τ,x)满足: (14) 考虑初值条件ρ0,j0∈Hk(),使得假设方程(5)的整体光滑解不存在,且在有限时间T*>0处发生爆破,即对T0>0,有且对任意τ∈T0,T*,有 由于Nε(T0)<1/(2c0),则存在T1∈T0,T*,使得Nε(T1)<1/(2c0),利用(14)式,有Nε(T1)≤1/(4c0),由此产生矛盾. 这里参数c与ε无关. 这是在新的时间尺度下的先验估计,利用变量替换就完成了定理1的证明. 令(ρ,j)为(5)的光滑解,对于给定的与ε无关的初值,改变时间变量,令: 新变量满足下面方程: ∂tρε+∂xjε=0 (15) (16) (17) 令(17)式左边ε→0,得到在D′+×中,有⇀0,将其带入到(15)式中,得到在D′+×中,有 (18) 令T>0,(15)式表明∂tρε在L2+;Hk-1上有界,此外,在C+;Hk中有界,因此在L20,T;Hk-1中有界,于是在H10,T;Hk-1上一致有界.我们得到:存在子列εn→0和使得H10,T;Hk-1且在H10,T;Hk-1上有:⇀则我们有且有ρεn|t=0=ρ0. 由经典结论表明,整个序列(ρε-r)在H10,T;Hk-1上弱收敛到0.且当ε→0时,在D′+×中有ρε⇀r. 令0 由于ρε的子列在C0,T;Hk′I中的极限值也是在分布D′0,T×I中的极限值.非线性扩散方程(4)在空间C0,T;HlI,l>3/2内存在光滑的整体解,参考[14]中第十五章.于是,在C0,T;Hk′I中,有ρε子列的极限等于r.因此得到ρε在空间C0,T;Hk′I中的收敛性,即:在C0,T;Hk′I中,有ρε→r. 运用流函数(Stream函数)[15],证明定理2中的收敛速度估计.由前面的能量估计,我们知道ρε关于ε一致有界,jε在L2(+;Hk())上一致有界. 令r(t,x)为(4)的解,我们有如下方程: (19) 将(16)式变为: (20) 定义流函数 zε(0,x)∶=0 记右端三个积分为A、B、C,利用Cauchy-Schwarz不等式,分别估计为: 于是: p(x)-p(y)(x-y)≥mx-y2,m=infp′(ξ),ξ介于x,y之间 这里c只依赖于T,与ε无关.于是有收敛速度估计: 本文讨论了Carleman类方程在常状态附近的光滑解的整体存在性,并收敛于非线性扩散方程的解.在能量积分的框架下,统一了Kurtz、Lions、Toscani等人的工作,并将α的限制去除.除此之外,通过流函数以及解的一致先验估计获得了Carleman类方程的解收敛于扩散方程解的速度,这是Carleman类模型渐近问题中首个关于速度的结论.2 一致适定性
2.1 初步转化
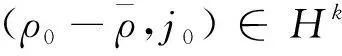
2.2 能量估计



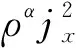

2.3 定理1最后的证明



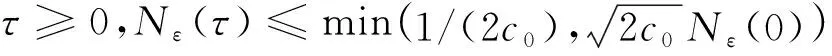

3 渐近分析
3.1 极限方程

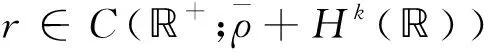

3.2 收敛速度

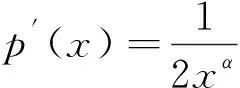

4 结 语

