考虑时空分布的电动汽车充电控制策略

黄 珊 郭秀娟

(吉林建筑大学 电气与计算机学院,长春 130118)

随着能源短缺的日益严重和环保呼声的高涨,电动汽车(Electric vehicle,EV)作为一种低碳、清洁的交通工具,受到各国政府的高度关注[1].

电动汽车具有：① 充电负荷较大,充电时间长；② 所有权归于用户,难以进行集中式管理；③ 在行驶中,具有时空分布不确定性等特点.当电动汽车大规模投入使用时,其连入电网的充电负荷会对电力系统的运行与规划产生很大的影响(比如电能损耗、运营成本[2]及谐波污染[3]等).准确的电动汽车负荷特性分析和高精度的电动汽车负荷预测具有重要意义[4],因此,本研究对应的充电策略是目前的首要任务.

1 智能交通系统与OD矩阵简介

智能交通系统又称智能运输系统,是将先进的信息技术、数据通信技术、传感器技术等有效地综合运用于交通运输管理体系,建立大范围、全方位、实时、准确、高效的综合运输管理系统.通过行人、车辆、道路的和谐配合提高交通运输效率,缓解交通阻塞,提高路网通过能力,减少交通事故,降低能源消耗并减轻环境污染.智能交通系统中的关键技术是反映特定时段内随时间变化交通需求模式的OD矩阵，对OD矩阵进行学习、探讨及应用,将有利于交通环境改善.

OD调查,即交通起点与终点间交通出行量的调查.特点是将人车货的出行活动视为交通形成细胞,由此研究交通的产生与分布.本文运用车辆OD调查,并将研究区域划分为5个部分.OD调查通常用一个二维表格表示,称为OD表(或OD矩阵).OD矩阵是交通网络中所有起点与终点之间出行交换数量的表格,反映用户对交通网络的基本需求,描述特定时间段内一个交通网络中所有起点到终点的交通出行量[5].

2 计时空分布的电动汽车充放电模型

2.1 电动汽车的特性

以交通使用为基础对电动汽车进行分类,分为私人拥有、公有、退休或是失业者拥有3种[6]，并根据分类确定电动汽车行驶模式.引入OD分析,旨在电动汽车行驶的起点和终点确定电动汽车的流动性和城市的交通出行量.由于私人拥有型电动汽车通常是在家和工作地点间行驶,途径简单,本文选择此类电动汽车进行研究.选择型号：L7e(货物运输车)；M1(轿车)；N1(货物运输车)；N2(货物运输车)这4种电动汽车作为研究对象.研究假定电池60%是锂离子,40%是铅酸.

根据调查得到的电动汽车电池容量数据,设每种类型电动汽车(L7e,M1,N2,N2)的电池容量，按式(1)和式(2)计算，得到各项参数(见表1).

表1 电动汽车电池容量的最适概率密度函数Table 1 Optimal probability density function of battery capacity for electric vehicles

(1)

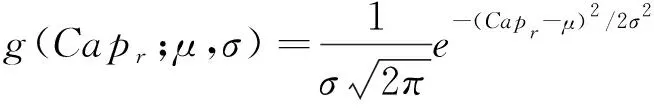
式中,Capr为每辆电动汽车的电池容量，kW·h；α为形状参数；β为尺度参数；μ为位置参数；σ为尺度参数；Γ(α)为伽马分布.

对调查得到的不同类型的电动汽车最大行驶距离通过多项式拟合，确定最大行驶距离和电池容量之间的关系,便于完善时空模型的数据库.

2.2 OD分析

OD分析是一种使用广泛的交通运输规划方法[7].通过OD分析研究时空模型中区域的地理信息、电动汽车的数量和电动汽车移动性等信息.

利用Trans CAD软件模拟研究城市,将城市分为5个区域，并将所研究城市的3种类型的功能区(住宅区、商业区和工业区)合理分配到5个区域内.

在交通规划中,质心代表功能区的几何中心.在时空模型中,两区域间的距离Dij由式(3)的正态分布得到：

Dij=N(μij，σij2) (3)

式中,μij是质心i和j间的直线距离,m；σij是考虑驾驶员喜好的路径选择标准偏差.

用ts和tf分别代表电动汽车1天内第1次行驶的起始时间.根据本文选择的电动汽车类型,假定1天只有2次行驶,ts和tf分别为电动汽车从家到工作地点的往返时间.

在一个特定城区内,OD矩阵是用来模拟1天内电动汽车从初始位置到终点的流动性.

在模型中,为便于OD矩阵分析，设如下变量：

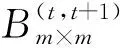
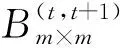
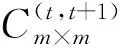
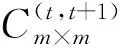
(4)

2.3 电动汽车的充电负荷

根据以下步骤确定电动汽车的充电负荷.

对于每辆电动汽车,蒙特卡洛模拟的作用是生成相应的最适合概密度函数和约束电池容量.如果产生的电池容量不在规定的容量范围内,将重复此步骤,直至满足约束条件.在以上产生每辆电动汽车电池容量的基础上,每辆电动汽车相应的最大行驶距离由Capr与Ran之间的关系决定.

利用OD分析模拟电动汽车1天的活动.电动汽车1天内行驶时间ts和终止时间tf的分布如图1、图2所示.由图1曲线可见,电动汽车的起始时间基本上全部在早晨7～8点左右的早高峰时间段；由图2曲线可见,电动汽车的终止时间基本上全部在下午4～5点左右的晚高峰时间段,在晚上9～11点的时间段也出现了一个小高峰.

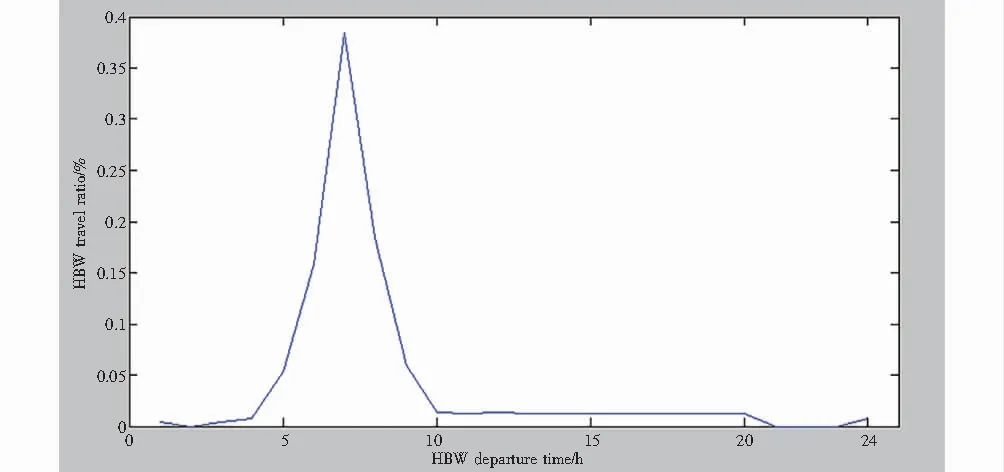
图1 HBW 1天内行驶的起始时间Fig.1 HBW starting time in a day

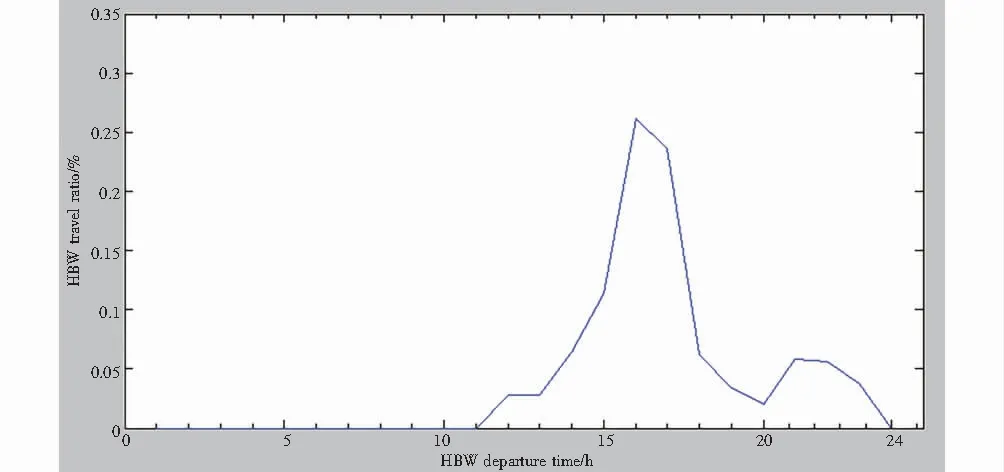
图2 HBW 1天内行驶的终止时间Fig.2 HBW termination time in a day

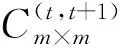
2.3.1 确定慢速充电的开始时间tsc

tsc是确定电动汽车充电负荷时间分布的关键参数.电动汽车的充电时间由人们的日常交通出行和电动汽车的充电策略决定.本文采用两种充电策略确定慢速充电开始时间tsc.

(1) 无序充电策略. 默认电动汽车日常行驶结束回到家以后立刻开始充电，即慢速充电的开始时间tsc等于电动汽车行驶的完成时间tf,如图2所示.

(2) 有序充电策略[8]. 设想有一个基于双递阶控制结构的主动管理系统,一边由聚合商领导,另一边由系统运营商控制.进一步假定电动汽车的充电负荷根据聚合商的市场谈判或根据系统运营商需要控制.公式(5)描述了考虑研究区域实时交通数据和实时电价数据情况下智能充电的随机模拟,其中μ代表凌晨1点,σ代表5小时的时间.由此结果可知,与无序充电策略相比,智能充电策略实现了将电动汽车的充电负荷从系统的峰值时间转到低谷时间.

(5)

2.3.2 确定电动汽车充电时的荷电状态(State of capacity,SOC)

设SOC与行驶距离呈线性下降的关系,t时刻电动汽车的电池容量为SOCt,是通过ts进行每小时追踪SOC得到的,通过式(6)和式(7)计算得出：

SOCt=η·[SOCt-1-D(t-1,t)(i,j)/Ran]t>ts(6)

SOCts=SOC0(7)

其中，SOC0是电动汽车的初始SOC,变化在[0.8,0.9]范围内(80%～90%的SOC维持电池寿命)[9]；引入能源效率系数η,变化在[0.9,1.0],表示现实社会交通中加速和减速过程给电动汽车带来的能量损失.当电动汽车开始充电时,设此时的电池容量为SOCc,即：

SOCc=SOCtsc(8)

利用蒙特卡洛模拟在以上步骤中确定tsc和相应的L(r,tsc),L(r,tsc)的电力需求,利用文献[10]提出的方法计算.

若有n辆电动汽车,则需按照上述步骤重复n次.记录每个电动汽车1天内在L(r,t)的充电负荷.当m(m≤n)辆电动汽车在L(r,t)的充电负荷被记录时,总的电动汽车充电负荷PT为：

(9)

2.4 时空模型中的假设

在时空模型中进行如下假设，当出现符合下列两者中任意一个标准的情况时,终止蒙特卡洛模拟的运行：

(1) 迭代次数达到最大值；

(2) 两个顺序迭代之间电动汽车充电负荷足够小时，如式(10)所示：

(10)

式中,Li为关于每个区域24小时内电动汽车充电负荷的矩阵；NMC表示迭代次数,ε是收敛因子.设定ε为0.001,NMCS为迭代次数的最大值,设定为10.当满足式(11)的标准时进行快速充电.

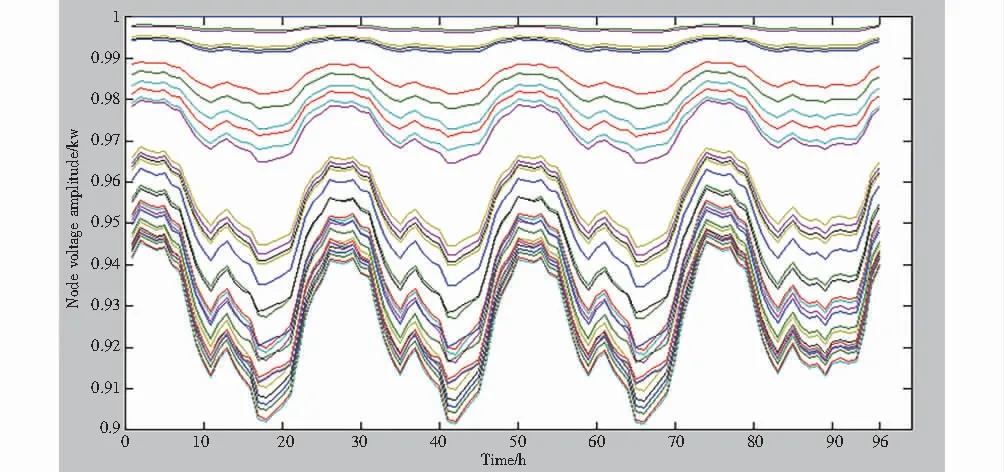
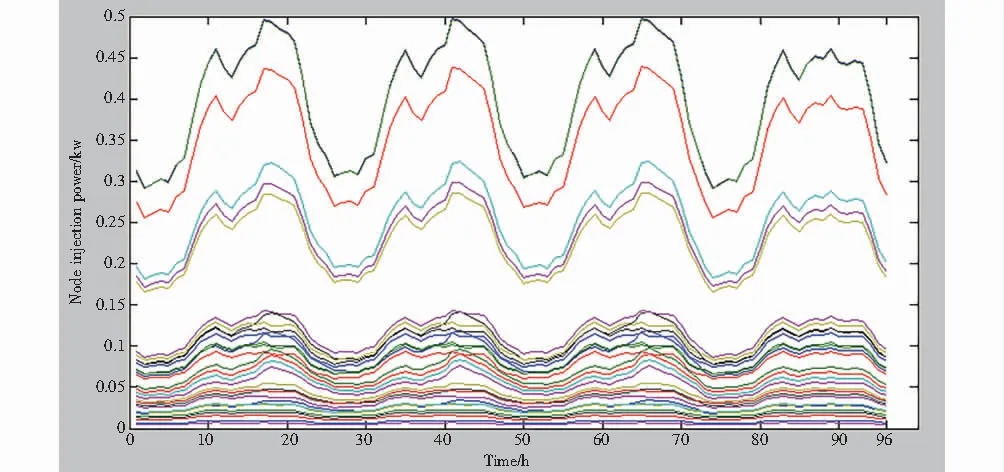
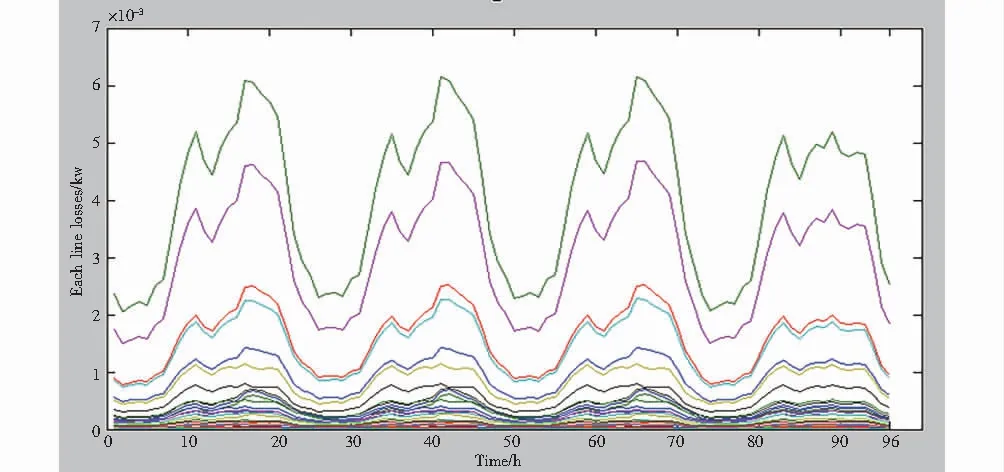
SOCr<0.2orD(SOCr)

式中,SOCr为实时的SOC；Dwh为工作地点和家之间的直线距离，m；D(SOCr)代表使用现有的可用电池容量能够行驶的距离，m；为保持电池寿命,电池容量SOC不应低于0.2[11].

每个区域Lr可能包含多条母线,当区域Lr内所有电动汽车的充电负荷在t(1≤t≤24)时刻被设定好时,获得电动汽车的所在位置对分配其充电负荷到一个特定的网络母线上是极其重要的.例如,如果电动汽车在t时刻停在了一个住宅区内,电动汽车的充电负荷将被分配到这个区域的所有母线上,然后在时间t的时候按比例将电负荷供给普通住宅.该方法同样适用于其他区域的电动汽车.

2.5 时空模型的构建

使用MATLAB软件,模拟某城市的5个区域内不同类型的电动汽车3天的行驶状况,城市的交通流量的模拟在Trans CAD中进行.根据模拟城市规模,设定电动汽车的数量为1 000辆,假设每种电动汽车具有相同的市场占有率；将SOC设定为最小,为保持电池的寿命,SOC不低于0.2；考虑到电池荷电状态具有时序耦合的特性,车辆出行时间分布具有随机性,为提高模拟结果的准确性,将模拟运行时间设定为4天96小时.

3 算例分析

本算例利用Trans CAD中的UTOWN案例模拟HBW电动汽车4天96小时的行驶情况,并算出电动汽车的充电负荷.该模拟城市内有5个区域(包含住宅区,商业区和功能区3个区域)，每个区域可能有一个或者多个功能区.利用无序和有序两种不同的充电策略,充电方式有慢速充电和快速充电.由于模拟的城市区域范围较小,电动汽车的数量不是很多,所以电动汽车几乎全部符合慢速充电的条件.本算例采用慢速充电方式，每小时OD矩阵是从Trans CAD的UTOWN案例中,通过Time of day analysis分析得到的.

采用IEEE 33节点配电网算例.电动汽车负荷接入节点4,11,12,15,26.已知基础日负荷如图3所示.采用前推回代法进行潮流计算,对比分析接入电动汽车前后配电网网损、节点电压等情况.

图4是“dumb”充电策略下各支路节点电压幅值曲线.从图中曲线可以看出,在第18小时、第42小时、第66小时和第90小时左右,都出现了电压幅值急速下降的现象.由于选择的电动汽车类型是HBW,只在家和工作地点间行驶,电压幅值急速下降的时间与正常下班回家的时间相吻合,由此可知,电动汽车的普及更容易导致住宅区产生低电压.

图3 日负荷(标幺值)Fig.3 Daily load (per unit value)

图4 节点电压幅值Fig.4 Node voltage amplitude

图5 各节点注入功率Fig.5 Injection power of each node

图6 各个线路损耗Fig.6 Each line losses

图7 慢速充电的充电负荷Fig.7 Charging load for slow charging

图5和图6分别代表各节点的注入功率和各线路的损耗.图5中的注入功率包括负荷功率和线路损耗两部分.分析图5、图6也能看出,在第18小时、第42小时、第66小时和第90小时左右,功率都出现了峰值,可见，电动汽车的充电负荷对电力系统配电网的影响不容小觑.

图7是电动汽车在慢速充电情况下的充电负荷.图7为三维立体图,x轴表示时间,y轴代表模拟城市中的5个区域；z轴表示电动汽车在慢速充电的充电方式下的充电负荷.从图7中可以看出，区域5在下班时间的时间段充电负荷达到最大值,由于电动汽车的类型是HBW,即可推测出区域5是住宅区；区域2和区域3在下班时间段内的充电负荷也比较高,由此可推测出2个区域包括住宅区和商业区的两种功能区；区域1和区域4的充电负荷相对较低,可推测两区域应为工业区或包含工业区和商业区的两种功能区.

4 结语

本文研究的时空模型评估了大规模电动汽车的部署对城市配电网的影响，利用OD分析减少由电动汽车流动而产生的不确定性；通过对市场电动汽车的调查和分析,了解广义上的电动汽车特性,在时空模型中运用蒙特卡洛模拟得到不同时刻各个线路上电动汽车的充电负荷.时空模型能够提供节点电压和支路负荷的平均值及概率值,由此证实电动汽车连入电网进行充电对配电网有着一定程度的影响.此外,文中提及的时空模型对电力系统的规划和评估有较大帮助.与以往这方面的研究相比较,时空模型能够提供更为真实的模拟结果,因为使用了智能交通研究中的OD分析技术,在时间和空间两个维度上更准确地模拟了电动汽车的移动性.