飘带景观天桥静载试验及分析

陈 世 九

(福建船政交通职业学院,福州 350001)

0 引言

对桥梁进行静载试验,其目的是为了分析桥梁结构的承载能力和稳定性[1].根据桥梁的质量评定数据与结果,可以及时对施工过程中所存在的问题进行调整,可以用于指导桥梁运营的维护与管理.对于一些通行量较大的桥梁,也可以定期进行静载试验,以此为依据进行桥梁改造,及时修复因承载过重而引发的断裂问题[2],进而不断提高桥梁的承载能力.

1 工程概况

某人行景观天桥位处福建省,桥梁在平面布置上呈现飘带状,跨越江滨路.全桥为七跨一联连续梁桥,桥梁全长97.50m,各跨为(5.80+29.30+15.30+15.00+15.00+13.00+4.10)m.桥面宽2.95m,设双向1.5%横坡,横向布置为:0.20m花槽+0.15m栏杆+2.25m人行道+0.15m栏杆+0.20m花槽.

桥梁上部结构采用Q345qC钢箱梁,梁高均采用1.0m.主箱梁顶板厚16mm、底板厚18mm、腹板厚14mm,箱内顶、底板及腹板上布置扁钢加劲肋,加劲肋版厚10mm.箱梁横隔板间距2.0m,靠近横向联系处加密,横隔板厚10mm或14mm.桥墩采用Y形墩和圆柱墩.

根据甲方委托要求,依据《城市桥梁检测与评定规范》(CJJT 233-2015)和结构受力特性,对人行天桥第1联桥跨结构的受力控制截面进行荷载试验,测定试验荷载作用下控制断面的挠度、应变变化情况,评价该桥承载能力是否满足设计荷载5.0kN/m2(人群)等级要求.

2 静载试验

为能准确分析桥梁的整体受力规律及其使用性能,特采用MIDAS-Civil分析软件进行空间受力分析,对各种工况作用进行理论计算,并通过理论值与实测值进行对比分析,对桥梁结构的状态进行评估[3].

2.1 有限元建模

根据桥梁设计施工图纸,对桥梁进行MIDAS-Civil建模,并将人群设计荷载按5.0kN/m2×2.95m=14.75kN/m的均布荷载，按车道线布载进行计算,其弯矩内力图如图1所示.根据内力图所示,横跨江滨路的主桥第一联第二跨钢箱梁结构跨中截面的弯矩为最大,2#墩位处结构负弯矩为最大.

图1 设计荷载内力Fig.1 Internal force diagram of the design load

根据结构的安全性以及受力情况,选择主桥第一联第二跨钢箱梁结构的跨中截面(Ⅰ-Ⅰ截面)和2#墩位处(Ⅱ-Ⅱ截面)为测试截面(受力控制截面)进行静载试验,具体见图2.

图2 测试截面示意图(单位：m)Fig.2 Schematic diagram of the testing section

2.2 试验荷载

常用加载设备主要有3种,分别为车辆荷载、重物与专用加力架[4].根据桥梁设计资料和现场实测资料,利用MIDAS-Civil模型,以人群设计荷载(5.0kN/m2)为试验荷载产生的项目最不利效应值等效换算,确定了所需的试验荷载、加载位置[5].本试验中加载物采用水箱抽水配重进行等效加载.加载水箱采用钢板搭设,内铺防水薄膜,水箱尺寸为8.00m×2.25m,如图3所示.

图3 水箱加载现场照片Fig.3 Scene photo of the water tank loading

按照每级水位一定高度分3个级别进行分级加载,累计加载重量为9.000t，13.500t，18.000t.有限元模型试验荷载加载图如图4所示.

图4 有限元模型试验荷载加载图Fig.4 Test load diagram of finite element model

2.3 试验效率

根据《城市桥梁检测与评定规范》(CJJT 233-2015),桥梁静力试验用荷载效率η来确定试验的最大荷载[6].静力试验荷载效率η的计算公式为:

(1)

式中,Sstar为在静力试验的实际工况荷载作用下,控制截面的最大内力或变位计算值;Sk为控制荷载作用下,控制截面最不利内力或变位计算值;μ为设计冲击系数.

各试验工况下使用公式(1)计算控制截面在设计荷载和试验荷载作用下的弯矩值,计算结果见表1.结果表明,桥梁控制截面的静载试验荷载效率η满足规定的要求[7](对验收性荷载试验,其值应大于或等于0.85,且不得大于1.05).

表1 荷载效率计算Table 1 Calculation table of load efficiency

2.4 试验结果

在I-I截面处桥面位置左右两侧布设5m塔尺,采用精密水准仪测量测定试验荷载作用下该截面的挠度变化情况.在I-I和II-II截面处,在钢箱梁底面及腹板位置安装应变传感器,用静态应变仪采集,确定在此荷载条件下的实际应变[8].

在试验加载工况下,进行各控制截面挠度的实测工作,测试现场照片如图5所示.挠度实测值详见表2.

图5 挠度、应变测试现场照片Fig.5 Scene photos of deflection and strain testing

Test sectionsMeasuringpointMeasuredvalue/mmAveragevalue/mmHeoreticalValue/mmCheckcoefficientηResidualdisplacement/mmRelative residualdisplacement/%Section Ⅰ-ⅠRight side5.485.565.960.930.488.1Left side5.640.538.6

3 试验结果分析

3.1 挠度测试结果分析

挠度实测值及其与理论值的比较如表2所示.各分级荷载作用下,截面实测挠度值与理论值的比较以及挠度随加载重量的变化曲线见图6.

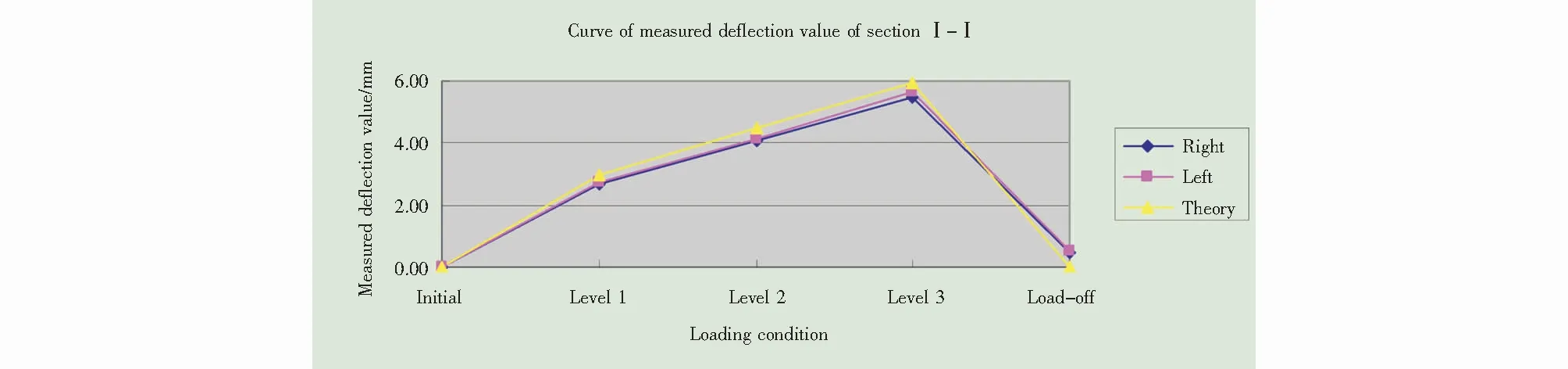
图6 截面Ⅰ-Ⅰ实测挠度曲线图Fig.6 Curve of measured deflection of section Ⅰ-Ⅰ

实测结构挠度校验系数η=实测挠度/理论挠度,是试验挠度的实测值与理论计算值之比,它反映结构实际承载能力的工作状态.相对残余变位Sp′=Sp/St×100%,用以描述结构整体或局部进入塑性工作状态的程度.从表2可以看出,I-I截面(第2跨跨中截面)挠度校验系数为0.93,相对残余挠度最大值为8.6%.测试截面挠度校验系数均小于《城市桥梁检测与评定规范》(CJJT 233-2015)规定的1.00,桥梁结构的承载能力满足要求;相对残余挠度最大值小于《城市桥梁检测与评定规范》(CJJT 233-2015)规定的20%.

由表2和图6可见,实测得到挠度值与理论计算值较接近,且分级加载过程中,实测挠度值随荷载线性增加呈线性变化,荷载作用下梁片处于弹性受力状态[9].

3.2 应变测试结果与分析

各控制截面的应变实测值及其与理论值的比较如表3所示.加载完毕时各分级荷载作用下,截面梁底实测应变值与理论值的比较以及应变随加载重量的变化曲线如图7、图8所示.

表3 各控制截面应变分析Table 3 Strain analysis table for the control sections

由表3可见,各控制截面应变校验系数为0.90～0.93,相对残余应变最大值为6.7%.测试截面应变校验系数均小于规定的1.00,相对残余应变最大值小于规定的20%.

图7 截面Ⅰ-Ⅰ钢箱梁底实测应变曲线图Fig.7 Curve of measured strain value at the beam bottom of section Ⅰ-Ⅰ

图8 截面Ⅱ-Ⅱ钢箱梁底实测应变曲线图Fig.Curve of measured strain value at the beam bottom of section Ⅱ-Ⅱ

由表3和图7、图8可见,实测应变值与理论计算值较接近,且分级加载过程中,实测应变值随荷载线性增加呈线性变化,荷载作用下梁片处于弹性受力状态.

4 结论和建议

综上所述,该人行天桥承载能力能满足设计荷载等级要求.为保证人行天桥的安全和桥梁结构的耐久性,建议如下:

(1) 营运中应注意加强对桥跨结构各受力控制截面、栏杆、支座等重要部件的定期监测和养护管理,并保持桥面铺装平整和路面的整洁,减小桥梁的冲击振动和跳跃振动.

(2) 定期对钢结构进行日常防腐、防锈检查,出现缺陷情况及时修补.

(3) 建立永久性的水准测量点,定期对上跨城市行车道的桥跨变位情况进行测量.