卧式埋地储罐稳定性研究

李玉坤, 林俊丞, 刘 浩, 姜 雪, 路太辉

(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580; 2.中国石化中原石油工程设计有限公司,河南郑州 450000; 3.河南省医药设计院有限公司,河南郑州 450000; 4.中国石油北京天然气管道有限公司,北京 100020)

埋地储罐作为汽油、柴油、液化石油气等燃料的常用储存容器,被广泛应用于油库、加油加气站等相关场所。埋地储罐的失稳破坏往往发生在强度破坏之前,其壁厚一般由外压稳定性计算来确定[1-4]。针对均布外压圆柱壳结构,Papadakis等[5]提出了经典薄壳理论;该理论不考虑径向应力及横向剪切变形。基于薄壳理论,Timoshenko等[6-7]推导出了各向同性薄壁圆柱壳失稳临界载荷计算公式。为考虑剪切变形的影响从而提高临界荷载计算精度,一阶及高阶剪切变形理论相继得到发展及应用[8-15]。结构的屈曲分析通常采用理论与有限元法相结合的方式进行研究。任宪骏等[16]研究了初始缺陷、加劲肋间距及大开孔对薄壁圆柱壳稳定性的影响;龙连春等[17-18]研究了加劲参数对圆柱壳屈曲承载力的影响;Zheng等[19-21]对变厚度圆柱壳进行了屈曲分析;Combescure等[22-25]对存在厚度缺陷的圆柱壳结构进行了稳定性研究;Shen等[26-31]对分层薄壁圆柱壳的静、动态稳定性进行了研究。工程中埋地储罐的设计主要依据压力容器规范,如中国的GB150-2011压力容器[32]及美国规范ASME Boiler and Pressure Vessel Code[33]。基于规范的稳定性设计只将储罐外部土压力简化成均布外压,难以反映储罐的真实外压。针对储罐实际受力情况,笔者提出将储罐覆土外压(包括地面载荷引起的外压)转换成罐壁径向力和切向力方法,并推导出计算公式;基于ANSYS特征值屈曲分析,提出储罐失稳临界埋深的确定方法及任意埋深储罐的失稳判定方法,有助于储罐埋深的合理化设计。

1 基于规范的稳定性设计

埋地储罐在无内压的空罐状态下极易发生失稳破坏,需对覆土外压及地面载荷作用下空罐进行稳定性校核[34-35]。校核公式为

[p]≥pc.

(1)

式中,[p]为许用外压,kPa,根据强度计算得到的有效壁厚和加强圈设置参数,按GB150中外压圆筒的相关公式进行确定;pc为计算外压,kPa。

在文献[35]中,计算外压取圆筒所受最大土压力,其作用点假设在距离圆心1/3R处,计算公式为

(2)

式中,γ为土体重度,kN/m3;R为圆筒半径,m;K0为土体侧压力系数;H0为储罐埋深,m。

2 埋地储罐土压力特点

埋地储罐作为一种大直径薄壁圆柱壳结构,针对其周围土压力分布的研究较少。根据Shmulevich等[36]的埋地圆柱壳实验,薄壁圆柱壳土压力分布如图1(圆柱壳覆土为不同压实程度的砂土)所示。

由图1可知,在圆筒上半部,自M点至N点径向力和切向力数值先增加后减小,二者最大值均发生在弧MN的中间段;径向力均为正值,切向力在M点与N点附近减小到零或负值,可近似认为在M点和N点处切向力为零。圆筒下半部切向力较小,可忽略其影响,认为仅受地基支撑作用。

图1 埋地圆筒周围填土作用力分布Fig.1 Soil pressure distribution around buried cylinder

3 径向力和切向力计算公式推导

将储罐简化为圆筒模型,忽略其附属结构。考虑罐体上半部覆土压力,对该结构进行受力分析,假设罐体顶部至地面的高度为H0,如图2所示。

图2 圆筒受力分析Fig.2 Stress analysis of cylinder

罐体上半部承受的土压力连续作用在罐壁,在罐壁上任取一点,将该点的土压力沿圆筒径向和切向分解。圆筒径向力σn和切向力στ计算公式推导如下:

(3)

σn=σsin(α+θ)=σ(sinαcosθ+cosαsinθ)=

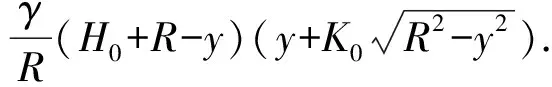
(4)

(5)

在圆筒上半部分选取若干点,根据上述公式求出该点径向力σn和切向力στ;然后将各点σn和στ值进行拟合,得到其近似函数表达式(关于x或y的函数),最后将函数表达式输入ANSYS中,利用SURF154单元将径向力和切向力施加在模型上。

4 储罐失稳临界埋深确定

失稳临界埋深指埋地储罐由于失稳而发生破坏时的埋置深度,即失稳破坏时地面到罐顶的距离。储罐失稳临界埋深可通过有限元软件ANSYS屈曲分析确定。储罐在空罐状态下的载荷包括径向力、切向力和自重。由于径向力和切向力为非均布表面载荷,不能进行非线性屈曲分析,因此通过特征值屈曲分析确定储罐的失稳临界埋深。

在特征值屈曲分析中,特征值表示给定载荷的比例因子。在特征值求解时,所有载荷进行相应缩放。径向力和切向力为非均布表面载荷,可进行一定比例的缩放;而自重为恒载荷,不需要进行缩放处理。因此,为保证储罐在失稳临界状态时所有外力均不被缩放,即储罐在真实外力作用下失稳,则应使特征值计算结果为1(或接近1,即允许一些收敛容差)。

为确定储罐的临界埋深,采用以下步骤:

(1)选取任意埋深,并在储罐上半部选择足够的点;

(2)将各点坐标带入式(4)和式(5),求得各点处的径向力σn和切向力στ;

(3)分别对σn和στ关于x坐标进行拟合,获得其函数表达式;

(4)建立储罐模型,对其施加径向力、切向力及自重载荷;

(5)利用ANSYS有限元软件对储罐进行特征值屈曲分析,获取特征值;

(6)如果特征值等于或接近1,则假设的埋深即为储罐临界埋深;否则,将假设埋深与特征值的乘积作为新的假设埋深并重复步骤(2)～(5)。

若存在地面载荷,则将其换算成均布载荷,并转化成当量土层厚度,按照上述方法求得的储罐失稳临界埋深应扣除当量土层厚度。若考虑工程实际中几何和材料非线性的影响,可引入安全系数,因此储罐的失稳临界埋深可确定为

(6)

其中

h=q/γ.

式中,HS为考虑安全系数后储罐的失稳临界埋深,m;H为不考虑当量土层时特征值屈曲分析得出的失稳临界埋深,m;h为地面载荷对应的当量土层厚度,m;q为地面载荷换算成的均布载荷,kN/m2;S为值大于1的安全系数,根据加油站及油库安全等级合理取值。

5 算 例

5.1 参数设置及模型简化

某埋地储罐,圆筒内径为3 m,长度为10 m,筒体壁厚为8 mm;封头为半球形封头,壁厚为10 mm;加强圈间距为2 m,截面形式选用矩形截面,其宽和高分别为18和80 mm。除加强圈外其余附属结构均忽略;储罐埋深为1.5 m,填土重度为18 kN/m3,土体侧压力系数K0为0.3。

在有限元软件ANSYS中圆筒模型采用SHELL63单元建立,加强圈模型采用BEAM188单元建立,载荷采用SURF154单元施加。材料本构模型采用线弹性模型,材料弹性模量E=2.06 GPa,泊松比μ=0.28。储罐上半部施加等效径向力和切向力,储罐下半部通过SHELL63单元的EFS参数设置模拟地基支撑作用。按照上述方法及设计参数,分别确定出无加强圈和有加强圈储罐的失稳临界埋深。

5.2 径向力及切向力计算

计算埋深1.5 m时储罐罐壁上的径向力。

如图2,在第一象限的1/4圆筒上,y坐标每隔1/15R选取一个计算点,将每个点的y坐标带入式(4),得出其径向力,通过拟合获得径向力关于y坐标的变化曲线,如图3(a)所示,函数表达式为

σn=-20.715y6+81.245y5-119.54y4+81.394y3-39.736y2+33.157y+16.176.

(7)

由式(5)计算可得各点处罐壁所受切向力。由储罐土压力特点分析可知,罐壁切向力在M和N点处均接近0,而由式(5)计算所得结果并不为0。从图1切向力变化曲线可知,在N点附近的一段圆弧上切向力近似关于y坐标线性变化,且该段圆弧在y坐标上的变化范围大致为[0,R/3]。因此,圆弧MN需分成[0,R/3] 和 [R/3,R]两段来分析。

图3 罐壁径向力和切向力关于y的变化曲线Fig.3 Curve of radial force and tangential force on y axis

在[0,R/3]段,切向力近似线性增加。在[R/3,R]段,M点处的切向力理论上为0,其变化曲线可以通过拟合区段[R/3, 14R/15] 数据和点(R, 0) 获得。通过式(8)(R/3≤y≤R)可知,当y=R/3时,切向力为37.943 5 kPa。为确保两段切向力变化曲线在连接点y=R/3处的连续性,区段[0,R/3]上的变化曲线可通过拟合点(0, 0) 和点 (R/3, 37.943 5)获得。在整个区间[0,R]上,罐壁切向力变化曲线如图3(b)所示,其函数表达式为

(8)

从式(7)和(8)可知,罐壁径向力在整个定义域[0,R]上对y的函数形式为高次多项式,其拟合曲线的相关系数R2为0.998 5,表明该曲线对罐壁径向力的拟合程度高,可以准确反映覆土压力在罐壁产生的径向力。罐壁切向力在[0,R/3]上线性变化,而在[R/3,R]上为高次多项式,高阶系数较大;两段曲线的相关系数R2分别为0.997 5和0.993 6,说明采用分段曲线对罐壁切向力进行拟合可靠性较高。将径向力与切向力叠加后的函数在整个定义域上仍为高次多项式,表明覆土压力在罐壁上呈高度非线性分布,且切向力与径向力为同一数量级,不可忽略。因此相关标准将土压当作罐壁上均布径向压力的处理方法不够准确,应采用本文中所述方法对覆土压力进行分解计算。

5.3 失稳临界埋深计算

5.3.1 无加强圈储罐

进行埋深1.5 m储罐的屈曲分析。提取前3阶模态,各阶模态的特征值依次为2.494 5、 2.651 9和 4.048 5。第一、二阶屈曲模态形状如图4所示,图示储罐变形图放大倍数为1.76,且在该工况下储罐变形区域横跨整个筒体,其失稳方式为整体失稳。

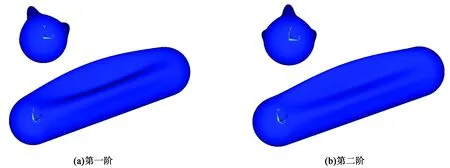
图4 无加强圈储罐第一阶和第二阶屈曲模态形状Fig.4 The first and the second buckling mode shapes of tank without stiffening ring

储罐埋深为1.5 m时,屈曲特征值为2.494 5。为使特征值接近1,将埋深进行相应放大,选取新埋深H0=2.494 5×1.5 m=3.7 m,计算出径向力和切向力并拟合出函数表达式,表示为

σn=-52.302y6+204.761y5-300.951y4+203.172y3-78.995y2+63.433y+28.019.

(9)

(10)

通过加载计算,储罐埋深为3.7 m时,前3阶模态特征值依次为1.082 9、 1.150 8和1.885 0,第一阶模态特征值已接近1。第一阶模态特征值略大于1,可知储罐的失稳临界埋深略大于3.7 m;选取埋深H0为3.8、3.9、4.0和4.1 m,加载计算得出其特征值分别为1.055 7、1.030 5、1.005 7和0.982 29。储罐埋深4.0 m对应的特征值接近1,而储罐埋深4.1 m对应的特征值小于1,因此无加强圈储罐的失稳临界埋深取4.0 m,屈曲形状与图4(a)所示第一阶屈曲模态形状基本相同。

5.3.2 有加强圈储罐

设置加强圈的储罐,失稳临界载荷一般较大,因此选取埋深H0=3.7 m,作用在罐壁上的径向力和切向力的函数表达式分别为式(9)和(10)。计算并提取前4阶模态,特征值依次为4.553 7、4.560 8、4.881 0和4.887 3;通过提取模态形状可知,第一、二阶屈曲模态,第三、四阶屈曲模态分别为同一种形式的失稳,其特征值基本相同。第一、三阶屈曲模态形状如图5所示,图示储罐变形图放大倍数为3.5,该工况下储罐变形区域集中在相邻加强圈之间的罐壁,储罐失稳方式为加强圈之间罐壁的局部失稳。

图5 有加强圈储罐第一阶和第三阶屈曲模态形状Fig.5 The first and the third buckling mode shape of tank with stiffening ring

储罐埋深为3.7 m时,载荷放大系数为4.553 7,重新选取埋深H1=4.553 7×3.7 m=16.8 m进行计算。储罐埋深为16.8 m时,前4阶模态特征值依次为1.018 8、1.019 6、1.093 0和1.093 9,第一阶模态特征值略大于1,可知储罐的失稳临界埋深略大于16.8 m;依次选取埋深16.9、17.0、17.1和17.2 m,加载计算得出其特征值分别为1.012 8、1.006 9、1.001 0和0.995 22。储罐埋深17.1 m对应的特征值接近1,而储罐埋深17.2 m对应的特征值小于1。因此有加强圈储罐失稳临界埋深可取为17.1 m,屈曲形状与图5所示第一阶屈曲模态形状基本相同。

加强圈对埋地储罐稳定性影响十分明显。储罐无加强圈时,其失稳临界埋深为4.0 m;相同条件下,在储罐筒体相距2 m设置一系列加强圈后,储罐失稳临界埋深增加至17.1 m。因此,对储罐埋深设计来说,加强圈可以有效地提高储罐容许埋深,增加储罐稳定性。

对于任一埋深储罐,若存在地面载荷,则可先将其转化为当量土层,将当量土层厚度和实际埋深之和作为储罐的当量埋深,计算当量埋深下罐壁各点径向力和切向力值并拟合出函数表达式,与自重载荷同时施加在ANSYS模型上,通过屈曲分析,获得第一阶模态的特征值(即ANSYS计算得出的频率,记为freq)及屈曲模态形状。对储罐进行失稳判定:若freq<1,储罐发生失稳;若freq>1,储罐不发生失稳;若freq=1,储罐处于临界失稳状态。因此,当freq=1时,储罐处于临界失稳状态,此时储罐埋深可作为储罐稳定性判据。

6 结 论

(1)将储罐简化为大直径薄壁圆柱壳结构,获取罐壁上部任一点在覆土压力下的径向力和切向力,建立的二者关于坐标y的非线性函数关系相较于现行标准储罐土压处理方式,该方法可反映罐壁上部真实受力。

(2)提出的储罐临界埋深完整的ANSYS计算方法可用于对储罐模型进行屈曲分析,多次迭代后屈曲特征值接近1,此时对应的埋深即储罐失稳临界埋深。

(3)加强圈对储罐失稳临界埋深影响显著。在本算例中,储罐无加强圈时,其失稳临界载荷为4.0 m;在储罐上沿长度方向相距2 m设置数个加强圈后,该储罐失稳临界埋深增加至17.1 m。在储罐结构上设置加强圈可大幅提升埋地储罐的稳定性,为储罐埋深设计提供充足的安全裕量。