考虑应力干扰的多簇压裂水平井产能分布规律

曾青冬, 佟 颖, 姚 军

(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.中国石化石油工程技术研究院,北京 100101)

水平井分段压裂多簇射孔是低渗透油气藏和非常规油气藏开采的关键技术[1]。裂缝扩展模型求解方法包括有限元方法[2]、扩展有限元方法[3-5]、位移不连续法[6-8]、离散元方法[9]等,较之于有限元类方法,位移不连续法求解速度更快。压裂水平井产能计算主要采用解析/半解析方法以及数值模拟方法[10-15]。上述产能计算方法中裂缝为平行直线裂缝,然而多簇裂缝同步扩展时为非平行弯曲裂缝,因此有必要考虑缝间应力干扰对多簇压裂水平井产能分布的影响。笔者首先基于位移不连续法建立水平井多簇裂缝同步扩展数值模型,基于此由位势理论和叠加原理构建多簇压裂水平井产量计算方法,并分析产量影响因素。

1 裂缝扩展模型

1.1 模型建立

建立如图1所示的水平井多簇裂缝同步扩展物理模型。假设岩体变形为线弹性,裂缝延伸符合线弹性断裂准则,考虑压裂液井筒摩阻和射孔摩阻,各个裂缝分流量动态变化。

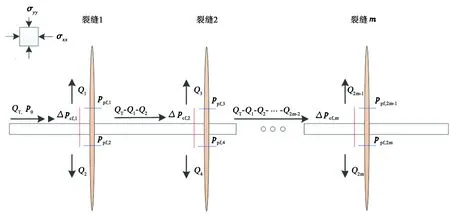
图1 水平井多簇裂缝同步扩展物理模型Fig.1 Physical model of multi-cluster fractures propagation in horizontal well

1.1.1 压裂液流动

压裂液包括在井筒和裂缝中流动,考虑井筒中流动须满足流量和压力关系。其中注入量须满足

(1)

式中,QT为总注入速率,m3/s;Qi为裂缝半翼i的注入速率,m3/s;m为裂缝条数。

考虑井筒摩阻和射孔摩阻,流体压力须满足

p0=pw,i+Δppf,i+Δpcf,i.

(2)

式中,p0为井筒跟部流压,Pa;pw,i为裂缝半翼i入口处流压,Pa;Δppf,i为裂缝半翼i射孔摩阻压降,Pa;Δpcf,i为裂缝半翼i井筒摩阻压降,Pa。

假设裂缝等高,忽略流体在纵向上的流动,裂缝宽度与裂缝长度相比较小,因此流体在每条裂缝上可以假设为一维流动,其运动方程为

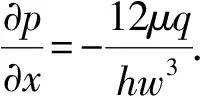
(3)

式中,q为截面流量,m3/s;w为裂缝宽度,m;μ为压裂液黏度,Pa·s;t为注入时间,s;x为沿裂缝扩展方向的位移,m;h为裂缝高度,m。

压裂液流动满足连续性方程:

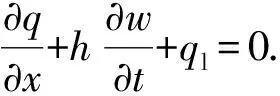
(4)

式中,ql为流体滤失速度,m/s。

方程(4)是局部守恒方程,建立全局守恒方程为

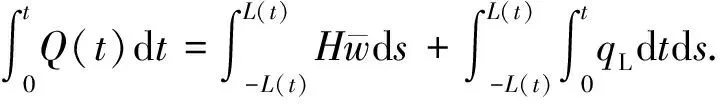
(5)

1.1.2 裂缝延伸

基于Olson[16]提出的三维修正系数,考虑有限高度对二维不连续方程的影响,其表达式为

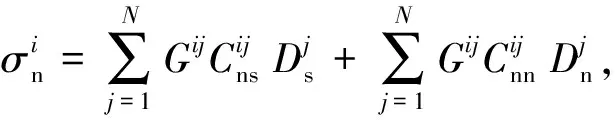
(6)

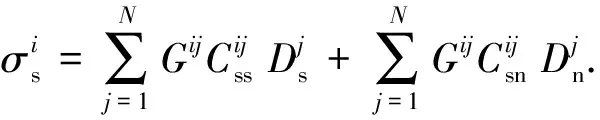
(7)

式中,σn为法向应力,Pa;σs为切向应力,Pa;Dn为法向位移不连续量,m;Ds为切向位移不连续量,m;C为弹性系数矩阵;G为三维修正系数。

裂缝扩展采用最大周向应力准则,当裂缝尖端综合应力强度因子超过岩石韧度时裂缝发生扩展,且裂缝扩展方向为

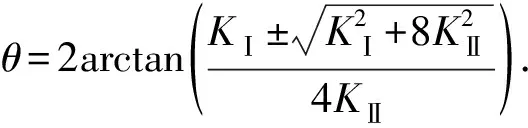
(8)

式中,θ为裂缝尖端偏转角;KⅠ为第一类应力强度因子,Pa·m1/2;KⅡ为第二类应力强度因子,Pa·m1/2。应力强度因子可采用尖端单元位移不连续量进行求解[16]。

1.2 数值求解

对压裂液连续性方程(4)在单元i上关于t在[t,dt]上积分,得到流体离散形式为

(9)

对流体运动方程(3)采用有限差分方法进行离散,得到裂缝单元间流量的表达式为

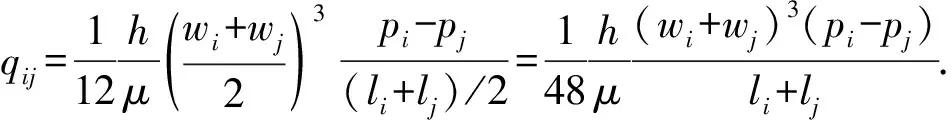
(10)

由于流动方程的非线性,须采用迭代方法进行求解。选择流体压力pi(i=1, 2, 3,…,N),裂缝分流量Qk(k=1, 2, 3,…, 2m),井筒跟部压力p0,时间步长dt为未知量。迭代求解思路为:假设未知量迭代初值,基于流体压力值pi利用位移不连续方程求解位移不连续量,即可得到裂缝宽度,由方程(9)可得N个方程,由方程(1)和(2)可得2m+1个方程,加上全局守恒方程(5)构成待求量的方程组,未知量个数与方程个数相等,采用牛顿迭代法即可求解上述方程组。

2 产能计算方法

当水平井多簇裂缝同步扩展时,裂缝不再相互平行,裂缝呈现弯曲延伸形态。基于裂缝扩展模型结果,裂缝由有限个直线段单元组成,通过叠加所有直线段单元上的位势得到势函数,分为裂缝无限导流能力和有限导流能力两种情形,构建了产能计算方法。

当裂缝与x轴平行时,根据位势理论,该裂缝所产生的势分布[17]为

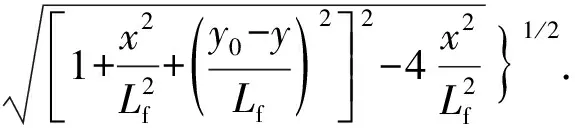
(11)

式中,Φ为裂缝产生的势,m2/s;C为常数;qf为裂缝产量,m3/s;Lf为裂缝半长,m;h为裂缝高度,m;B为体积系数;y0为裂缝中点纵坐标,m。

当裂缝倾斜时,如图2(a)所示,根据坐标变换公式,整体坐标系下势分布为

(12)

其中坐标变换公式为

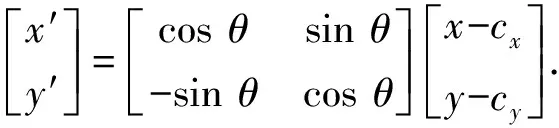
(13)

式中,(x′,y′)为局部坐标,m;(cx,cy)为裂缝中点坐标,m;θ为裂缝倾斜角,(°)。

对于任意形态的裂缝,如图2(b)所示,图2中裂缝仅为示意图,将其划分成N个单元,基于坐标变换公式和叠加原理可得储层势函数为

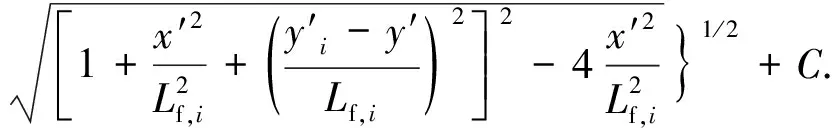
(14)

式中,qf,i为裂缝单元i产量,m3/s;Lf,i为裂缝单元i半长,m。

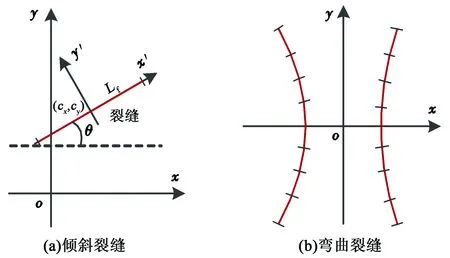
图2 裂缝示意图Fig.2 Schematic diagram of fractures

在供给边界(xe,ye),所有裂缝单元产生的势函数可表示为

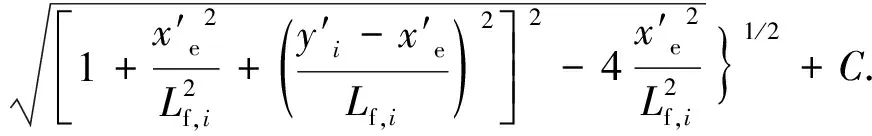
(15)

对于每一裂缝单元,其中点势函数可表示为

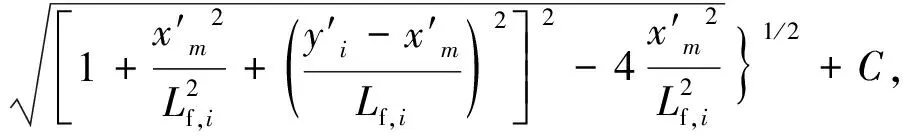
m=1,2,…,N.

(16)

势与压力的关系式为

Φ=kp/μ.

(17)

2.1 裂缝无限导流能力

考虑裂缝无限导流能力时,所有裂缝单元压力都为井底流压,方程(14)与(15)相减消除常数C,并将方程(17)代入左端,可得到N个方程:

(18)

当井底流压和供给边界压力已知时,求解线性方程组,可求得各裂缝单元产量,将所有单元产量求和即为井产量。

2.2 裂缝有限导流能力

如图3所示,对于任一裂缝单元j,裂缝单元节点坐标分别为(xj1,yj1)和(xj2,yj2),流体由(xj1,yj1)流向(xj2,yj2)。考虑裂缝有限导流能力时,采用达西公式表征裂缝单元节点压力和流量之间的关系[18],可表示为

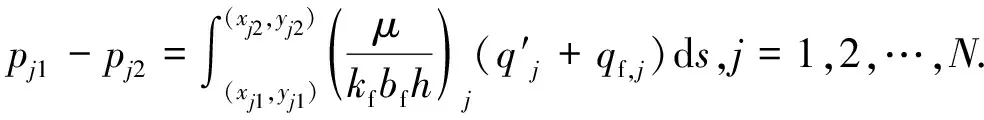
(19)

式中,kf为裂缝单元的渗透率,m2;bf为裂缝单元的宽度,m。

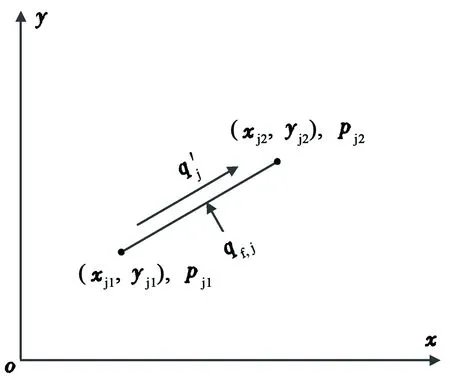
图3 裂缝单元流体流动示意图Fig.3 Schematic diagram of fluid flow in fracture element

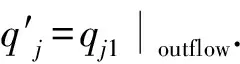
(20)

至于裂缝节点的流入流出量,必须满足流量守恒,因此可以简记为节点流量:

qm=qm|inflow=qm|outflow,m=1,2,…,Nv.

(21)

式中,Nv为裂缝单元节点总数。

以一条裂缝为例说明产量计算方法。如图4所示,水平井沿着x轴方向,裂缝与x轴交点为裂缝单元的节点。假设裂缝单元个数为N,则单元节点数Nv等于N+1。已知井底压力和供给压力,则未知量包括:单元产量qf,j(N个)、单元节点流量qm(N+1个)以及单元节点压力pj(N+1个)。

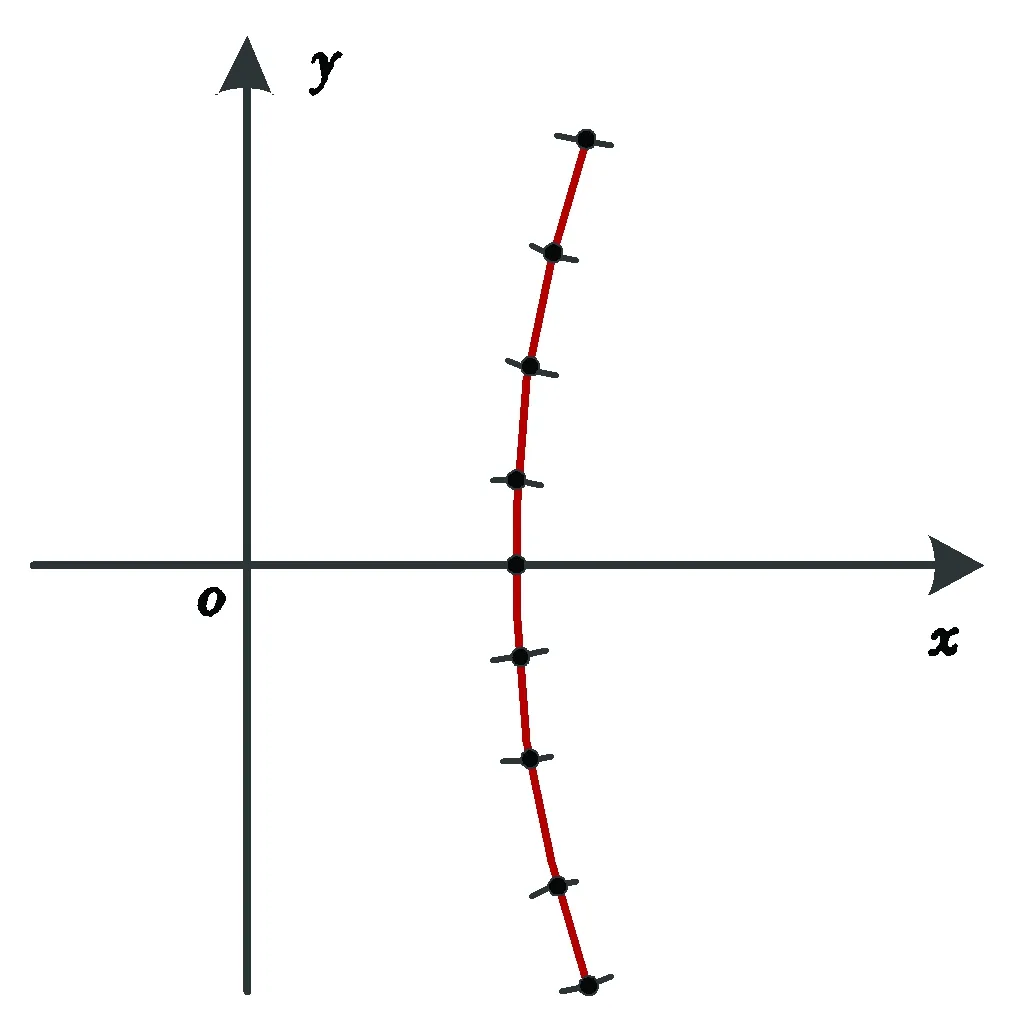
图4 一条裂缝产量计算示意图Fig.4 Schematic diagram of production calculation for one fracture

根据方程(19)可求出裂缝单元流入节点和中点的压降方程为

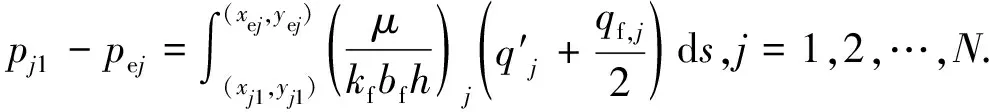
(22)

方程(14)与(15)相减消除常数C,并将方程(17)代入左端,可得到N个方程为

(23)

将方程(22)和(23)裂缝单元中点压力消除,可得到N个方程。根据裂缝单元压降式(19)可得到N个方程。

此外,针对裂缝单元节点流量,如图5所示裂缝单元i1和i2,裂缝节点为j1、j2和j3,节点j2的流量计算方程为

qj2=qj1+qf,i1.

(24)

裂缝尖端节点流量为0,因此基于式(24)可得到Nv(N+1)个方程。

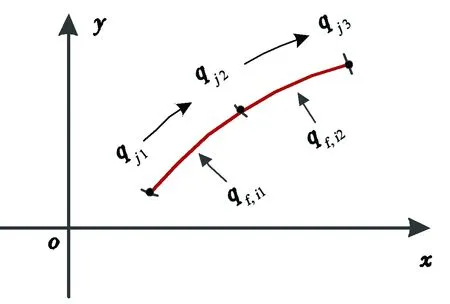
图5 裂缝单元节点流量计算示意图Fig.5 Schematic diagram of flux calculation for fracture node

当井底流压和供给压力已知时,与水平井相交的裂缝单元节点压力即为井底流压,因此综合上述3N+2个方程,与未知量个数相等,且为线性方程组,求解该方程组,即可求解裂缝单元产量,累加得到单条裂缝产量。采用相同方法可用于求解多簇裂缝产量,且根据井筒摩阻方程建立各裂缝入口节点压力之间的关系,可求解得到各簇裂缝产量。

3 算例结果分析

3.1 模型验证

为了验证裂缝扩展模型和算法的正确性,将滤失系数设为0,裂缝条数为1,比较数值解与KGD模型解析解。模型其他参数取值:弹性模量E为20 GPa,泊松比ν为0.25,注入速度Q0为0.027 m3/s,裂缝高度hf为15 m,压裂液黏度μ为0.1 Pa·s。KGD模型解析解详见参考文献[19]和[20],裂缝半长对比结果如图6所示。由图6可知,数值解与解析解相差很小,验证了裂缝扩展模型的正确性。

为验证产能计算方法的收敛性,计算对比了单一裂缝产量的解析解和数值解。模型参数取值:裂缝半长Lf为100 m,裂缝高度hf为15 m,基岩渗透率k为0.02 μm2,流体黏度μ为6 mPa·s,体积系数B为1.2,供给半径re为800 m,供给压力pe为30 MPa,井底流压pw为23 MPa。

单一裂缝产量数值解与解析解对比结果如图7所示。由图7可知,随着裂缝单元数目增加,数值解快速收敛于解析解,且当单元数大于10时,数值解与解析解之间的相对误差为0.04%,说明本文中计算方法正确有效。本文中数值解可用于求解多簇弯曲裂缝产量,此种情形下并无解析解,因此本文中的数值方法使裂缝产能计算更加完善,有必要进行研究。

图6 裂缝半长数值解与解析解对比Fig.6 Contrast of numerical and analytical solution for fracture half length

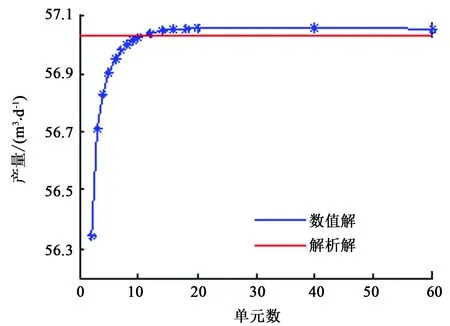
图7 单一裂缝产量数值解与解析解对比Fig.7 Comparison of numerical and analytical solution for single fracture production

3.2 产能影响因素

多簇裂缝同步扩展时,由于应力干扰的作用,裂缝沿非平面扩展,为此模拟不同间距时裂缝扩展结果并计算对比了应力干扰作用对产能的影响。通过裂缝扩展模型计算得到两簇射孔时裂缝扩展形态，结果如图8所示。模型参数取值:压裂液黏度μ为0.1 Pa·s,其他参数同前文。由图8可知,在应力干扰作用下,两簇裂缝相背离地扩展,且裂缝间距越小,扩展路径越弯曲。不考虑应力干扰作用是指裂缝扩展之间不存在任何互相影响,即裂缝扩展之间也不存在竞争,扩展的结果是所有裂缝都具有相同的几何参数(裂缝长度和宽度),且裂缝之间互相平行,不发生弯曲扩展,实际条件下是不可能发生这种情况的。

基于本文中的产能计算方法,仅计算一段内两簇裂缝产量,假设裂缝为无限导流能力,应力干扰作用对该段裂缝产量的影响结果如图9所示。模型参数取值:裂缝高度hf为15 m,基岩渗透率k为0.02 μm2,流体黏度μ为6 mPa·s,体积系数B为1.2,供给半径re为800 m,供给压力pe为30 MPa,井底流压pw为23 MPa。由图9可知,考虑应力干扰时产量高于不考虑应力干扰时产量,这主要是因为考虑应力干扰时裂缝之间相距更远,流体流动面积更大,说明裂缝扩展过程中的应力干扰作用有利于井产量的提高。

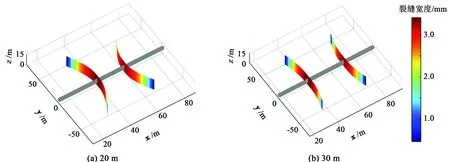
图8 不同间距时两簇射孔裂缝扩展结果Fig.8 Results of two-cluster fractures propagation for different spacing

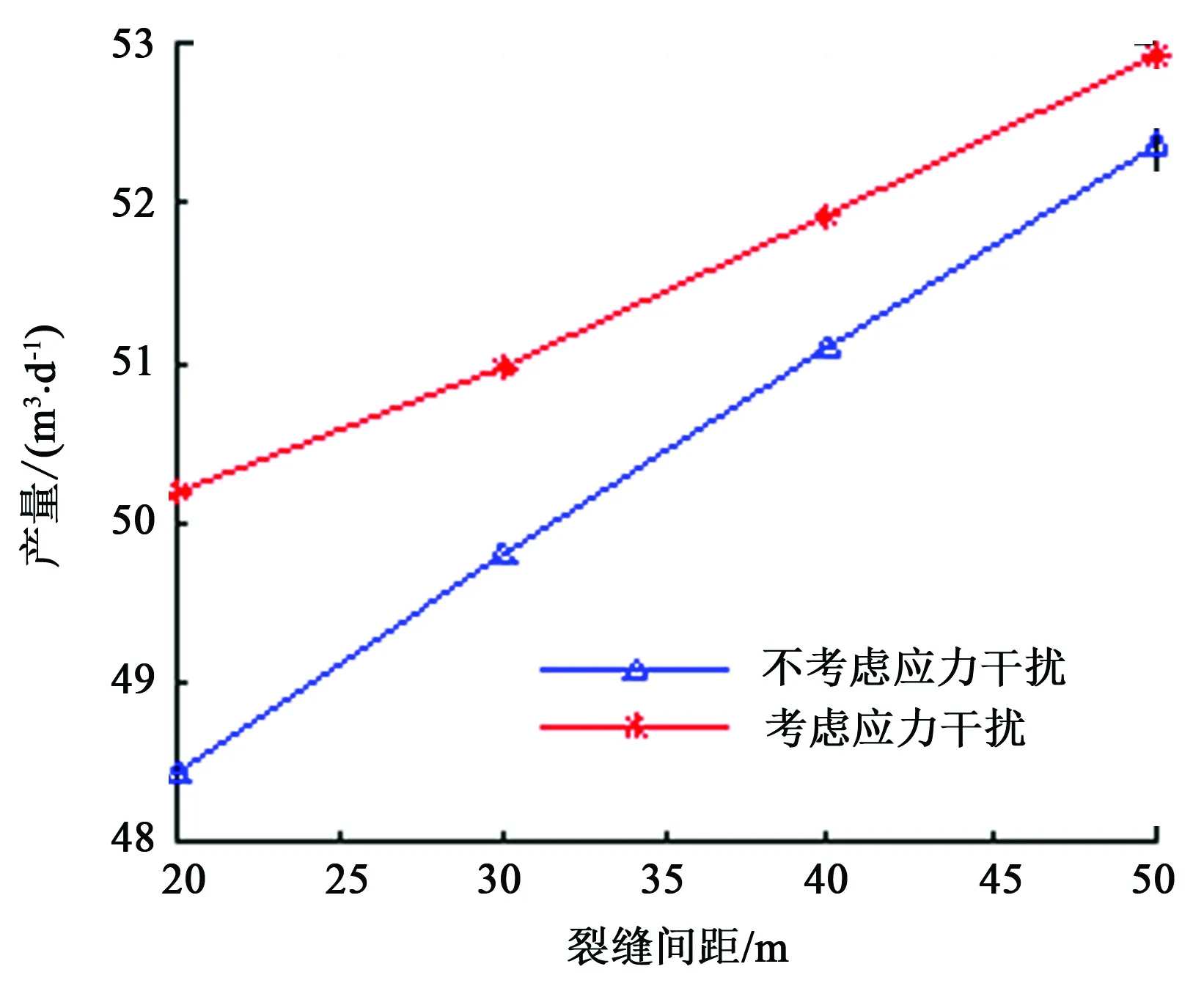
图9 两簇射孔应力干扰对产量的影响Fig.9 Effect of stress shadow on production of two-cluster perforation

同理,分析3簇射孔时裂缝扩展结果以及应力干扰作用对产量的影响,裂缝扩展模型与产能计算模型参数取值与前文相同,结果分别如图10和11所示。由图10可知,当间距较小时,中间裂缝长度和宽度将小于两端裂缝长度和宽度,说明应力干扰作用不仅影响裂缝扩展路径,同时影响裂缝几何长度。图11得到结果与图9相同,与此同时绘制了间距为20 m时3条裂缝贡献产量,如图12所示。考虑应力干扰对产量的影响主要作用在中间裂缝,这是因为考虑应力干扰时两端裂缝往外扩展,中间裂缝作用的流体流动面积增大,从而产量增加。

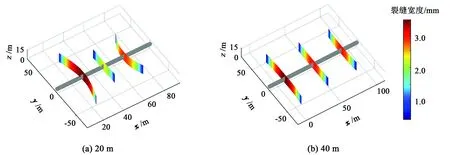
图10 不同间距时3簇射孔裂缝扩展结果Fig.10 Results of three-cluster fractures propagation for different spacing

计算分析裂缝间距和裂缝半长对产量的影响,结果如图13所示。由图13可知:裂缝间距越大,产量越大;裂缝半长越大,产量越大。此外,当增大裂缝间距时,3簇射孔时产量增加幅度大于两簇射孔产量增加幅度。而对于裂缝半长,3簇射孔时产量增加幅度与两簇射孔产量增加幅度相差较小。裂缝间距对产量的影响程度高于裂缝半长的影响程度。

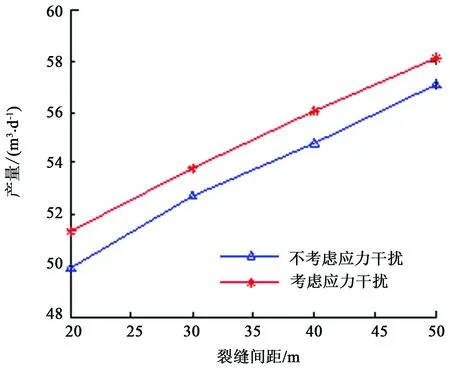
图11 3簇射孔应力干扰对产量的影响Fig.11 Effect of stress shadow on production of three-cluster perforation

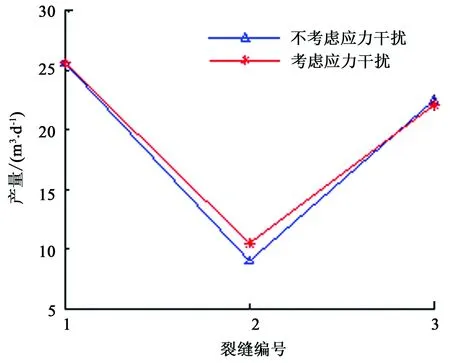
图12 各条裂缝产量结果Fig.12 Result of production for each fracture

根据裂缝扩展模型,还可以得到裂缝宽度分布,从而得到裂缝导流能力。基于此计算对比了3簇射孔时裂缝无限导流能力和有限导流能力情况下产量结果,如图14所示。由图14可知,考虑裂缝有限导流能力时产量略低于考虑裂缝无限导流能力时产量。

在实际生产过程中,裂缝闭合应力增大,导致裂缝导流能力降低,有学者对此开展了实验并拟合了曲线[21],得出表达式为

FC=10-2.758(σh-p)+0.219 1FCi.

(25)

式中,FC为当前裂缝导流能力,μm2·m;FCi为初始裂缝导流能力,μm2·m;σh为水平最小主应力,Pa;p为流体压力,Pa。

基于裂缝扩展模型求解得到的裂缝宽度,裂缝单元的导流能力可由立方定律计算得到,其渗透率计算公式为

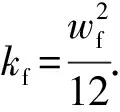
(26)

式中,kf为裂缝渗透率,m2;wf为裂缝宽度,m。

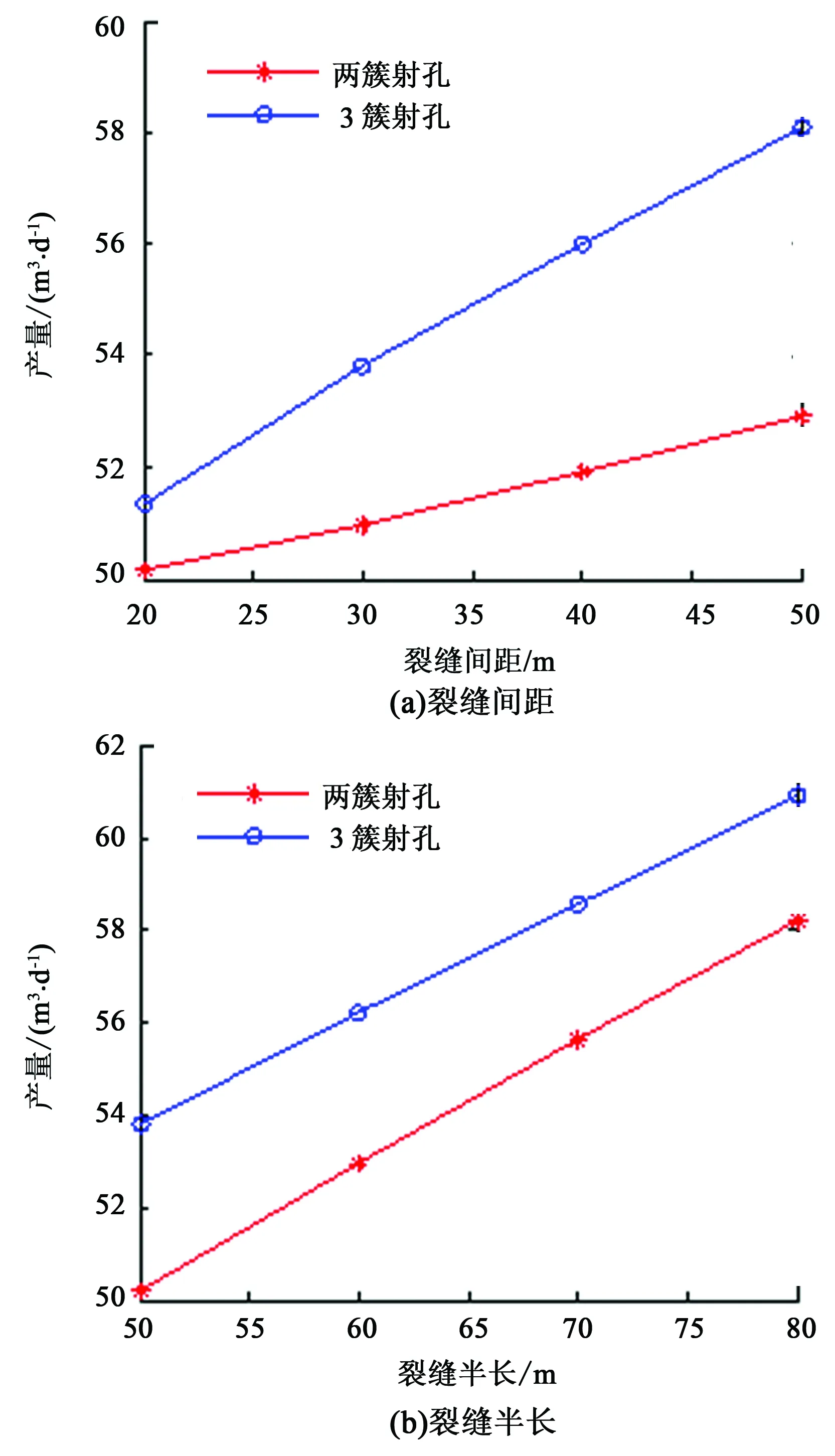
图13 裂缝间距和裂缝半长对产量的影响Fig.13 Effects of fracture spacing and fracture half-length on production

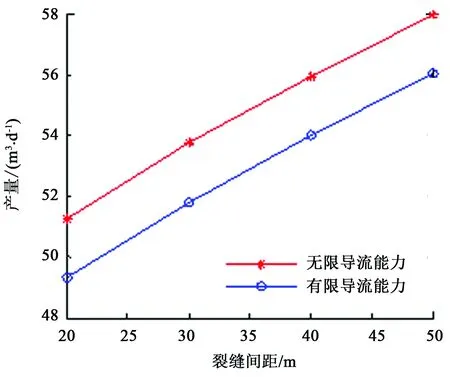
图14 裂缝导流能力对产量的影响Fig.14 Effect of fracture conductivity on production

储层水平最小主应力为38.6 MPa,计算对比了裂缝恒定导流能力和变导流能力情形下产量变化,如图15所示。由图15可知,考虑裂缝变导流能力时产量降低,而且随着生产压差增大,产量降低幅度增大,这是因为生产压差增大时,裂缝导流能力快速下降,但总体上产量相差不太明显,主要是由于基岩渗透率与裂缝渗透率相比很小,基岩往裂缝窜流量小,产量很大程度也取决于基岩渗透性。

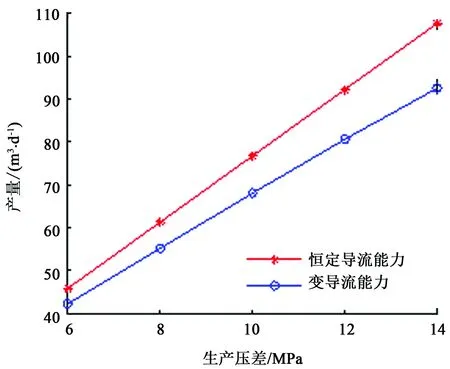
图15 裂缝变导流能力对产量的影响Fig.15 Effect of variable fracture conductivity on production

4 结 论

(1)多簇裂缝同步扩展时,应力干扰作用不仅影响裂缝扩展路径,而且还影响裂缝几何参数,导致裂缝扩展之间存在竞争性。

(2)裂缝扩展过程中的应力干扰作用有利于提高产量,主要原因在于应力干扰作用可使裂缝间距更大,获得更大的流动面积。

(3)随着裂缝间距和裂缝半长增大,产量增大,且裂缝间距对产量的影响程度高于裂缝半长的影响程度。

(4)考虑裂缝有限导流能力时产量低于考虑裂缝无限导流能力时产量,且考虑裂缝变导流能力时产量低于考虑裂缝恒定导流能力时产量。