考虑温度影响的摩阻扭矩计算模型及应用

张 辉, 谭天一, 李 军, 王 昊, 曾义金, 丁士东, 陶 谦

(1.中国石油大学(北京)石油工程学院,北京102249; 2.中国石油化工股份有限公司石油工程技术研究院,北京 100101)

钻柱与井壁之间的摩阻扭矩问题一直是钻井工程力学的核心研究课题[1-9]。随着常规油气藏的开采殆尽,长水平段水平井和大位移井的发展,对摩阻扭矩计算分析的精确性要求不断提高。对任何一种计算模型,摩阻系数的合理取值都是精确预测钻杆摩阻扭矩的必要条件。由于地温梯度的存在,地层温度随着深度的增加而增加,井眼温度亦随之变化。随着钻探领域的扩大,井眼深度不断加深,钻井循环温度对钻井过程的影响越来越不可忽视[10]。目前在钻井工程领域,通常将实测数据代入摩阻扭矩计算模型中迭代反算[11-13],采用单摩阻系数或分段摩阻系数,没有考虑温度对摩阻系数的影响,这导致预测值与施工中取得的实测值有较大偏差。笔者从涪陵页岩气焦石坝区块现场取回钻井液样本,考虑钻井循环温度为影响因素,通过室内实验得出钻井液润滑系数和泥饼黏滞系数随温度变化的规律[14-15]。管柱在井下受热产生热应力,在管柱上产生附加轴向力,建立考虑温度影响的摩阻扭矩计算模型,并应用该模型对焦石坝页岩气X井进行摩阻扭矩计算。

1 不同温度下钻井液润滑系数实验

1.1 实验样品和仪器

实验采用的样品为KCl聚合物润滑钻井液(水基钻井液)和柴油油基钻井液(图1),两种钻井液都从重庆涪陵焦石坝页岩气田钻井现场取回。根据现场资料,KCl聚合物润滑钻井液的配方为:水+3%膨润土+0.1%纯碱+1%防塌剂FT-388+1%水解聚丙烯腈钾盐K-HPAN+3%KCl+0.2%絮凝剂PAM+3%聚合醇+0.6%降滤失剂LV-CMC+2%超细碳酸钙;油基钻井液的配方为:柴油+1%有机土+2.5%主乳化剂HIEMUL+1.5%辅乳化剂HICOAT+3.5%降滤失剂HIFLO+3%油基封堵剂HISEAL+1%超细凝胶封堵剂+5%生石灰粉+重晶石。KCl聚合物润滑钻井液和油基钻井液各取10 L备用。实验使用的主要仪器为极压润滑仪,辅助设备为电热恒温油浴锅,如图2所示。

图1 KCl聚合物润滑钻井液样品和柴油油基钻井液样品Fig.1 Sample of KCl polymer drilling fluid and diesel-based drilling fluid

图2 极压润滑仪实验Fig.2 EP lubricity experiment

1.2 实验原理

如图3,极压润滑仪用一个钢摩擦环模拟钻杆,用带凹弧面的钢摩擦块模拟井壁,摩擦块通过夹持器固定,并使用扭矩扳手使摩擦块弧面紧贴摩擦环,施加正向压力,模拟钻井过程中钻杆和井壁之间的侧向力。将整个接触部分浸泡在待测液体中。电机带动摩擦环旋转,摩擦力在转轴上施加一个扭矩。测出该扭矩反算出钻井液的润滑系数,

T=FfR,

Ff=KN.

式中,T为扭矩值,N·m;Ff为接触面间的摩擦力,N;R为摩擦环旋转半径,m;K为钻井液润滑系数;N为正压力,N。

图3 极压润滑仪结构图Fig.3 Extreme pressure lubricity tester structure

1.3 实验设计

由于需要将钻井液加热到不同的温度进行测量,根据笔者实验时的室温条件,选取10 ℃为最低实验温度,每20 ℃为温度间隔,最高温度为90 ℃。其他实验操作与常规极压润滑仪实验相同,通过清水测定校正系数,再进行特定温度钻井液实验,最后计算出该温度下的润滑系数,

式中,α1为校正因子;Rw为清水值;Rm为钻井液值。

1.4 实验结果

根据结果可以得出,油基钻井液的润滑系数整体低于KCl聚合物润滑钻井液,但两种钻井液的润滑系数都随着温度的升高而增加。实验结果如表1、2所示。

表1 不同温度下KCl聚合物润滑钻井液润滑系数Table 1 Lubrication coefficient of KCl polymer lubricated drilling fluid at different temperatures

表2 不同温度下柴油油基钻井液润滑系数Table 2 Lubrication coefficient of diesel oil-based drilling fluids at different temperatures

润滑系数随温度变化的趋势线,如图4所示。

图4 两种钻井液润滑系数随温度变化的关系Fig.4 Relationship between lubricity coefficient and temperature

通过回归拟合,可得出两种钻井液润滑系数随温度变化的经验公式。其中KCl聚合物润滑钻井液润滑系数随温度变化的关系为

K=0.161 2+0.001T,

R2=0.961 7.

油基钻井液润滑系数随温度变化关系为

K=0.037 4+0.000 7T,

R2=0.985 8.

式中,T为温度, ℃;R为相关性系数。

对于回归方式的选择,分析认为本实验结果线性回归具有较高的相关性,且由于数据源不多,采取二次回归、三次回归等更高次的回归方式容易出现过拟合现象,故选择线性回归拟合。

2 不同温度下泥饼黏滞系数实验

2.1 实验样品和仪器

钻井液样品与极压润滑仪实验相同。实验仪器为泥饼黏滞系数仪和高温高压滤失仪。

2.2 实验原理

如图5,置于倾斜平面上的滑块所受重力可以沿着斜面的法向和切向分解,随着斜面转动增大切向分力克服摩擦力时,滑块开始滑动,此时正切值即为泥饼黏滞系数,即

Kf=tanα.

式中,Kf为泥饼黏滞系数;α为滑块滑动时斜面与水平面夹角,rad。

图5 泥饼黏滞系数仪滑块受力Fig.5 Forces on sliding block in cake frictional coefficient experiment

2.3 实验设计

图6 泥饼黏滞系数仪实验Fig.6 Cake frictional coefficient experiment

常规的泥饼黏滞系数仪实验(图6),要求使用API失水仪在中压(0.69 MPa)下滤失30 min制得泥饼,为了研究不同温度下泥饼的黏滞系数,实验中使用高温高压滤失仪分别在10、30、50、70、90 ℃中压条件滤失30 min制得泥饼,其他实验步骤与常规泥饼黏滞系数仪实验相同。

2.4 实验结果

根据结果可以得出,油基钻井液的泥饼黏滞系数低于KCl聚合物润滑钻井液系数,两种钻井液的泥饼黏滞系数都随着滤失温度的升高而增加。实验结果如表3、4所示。

表3 不同温度下KCl聚合物润滑钻井液泥饼黏滞系数实验结果Table 3 Result of KCl polymer drilling fluid cake frictional coefficient experiment at different temperatures

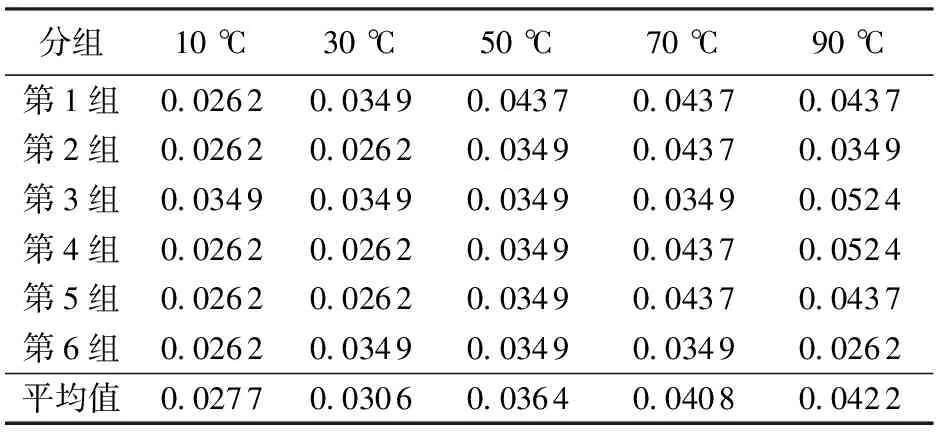
表4 不同温度下油基钻井液泥饼黏滞系数实验结果Table 4 Result of oil-based drilling fluid cake frictional coefficient experiment at different temperatures

绘制泥饼黏滞系数随温度变化的趋势线,如图7所示。

图7 两种钻井液泥饼黏滞系数随温度变化的关系Fig.7 Relationship between cake frictional coefficient and temperature

同样通过线性回归拟合出两种钻井液泥饼黏滞系数Kf随着温度变化的经验公式。KCl聚合物润滑钻井液的公式为

Kf=0.036 6+0.000 3T,

R2=0.986 1.

油基钻井液为

Kf=0.025 7+0.000 2T,

R2=0.969 4.

3 考虑温度影响的摩阻扭矩计算模型

对于摩阻扭矩的研究,目前国内外使用较多的有软杆模型、刚杆模型、有限元模型等[16-21]。考虑附加刚性力的修正的软杆模型误差相对较小,且便于计算,本文在其基础上进行研究。其每个单元段的轴向力计算公式为

扭矩计算公式为

M=μ(FE+Fn)LsR.

3.1 热应力产生的附加轴向力

温度改变时,物体由于外在约束以及内部各部分之间的相互约束,使其不能完全自由膨胀或者收缩而产生的应力称为热应力。管柱在井下受热作用,可将管柱单元段视作两端约束的空心管,故由于热应力产生的附加轴向力为

Ft=-βEΔTA.

式中,Ft为热应力产生的附加轴向力,N;β为材料的热膨胀系数, ℃-1;E为弹性模量,Pa;ΔT为管柱的温升, ℃;A为管柱横截面积,m2。

考虑热应力的单元段轴向力计算式为

3.2 受温度影响的摩阻系数

摩阻系数受到钻井液和泥饼润滑性的影响,通过实验可知钻井液润滑系数和泥饼黏滞系数随着温度升高而增大。由于地温梯度的存在,钻井过程中井筒内的温度随着垂深增加,故摩阻系数在不同深度也不相同。摩阻系数由两部分组成,即与温度相关部分和与温度无关的部分。旋转钻进时钻杆与井壁的摩擦形式与极压润滑仪相似,钻井液形成的润滑膜作用突出,其摩阻系数温度相关部分为润滑系数。滑动钻井钻进时钻杆和井壁的相对运动速度较小,泥饼对摩擦的影响明显,其摩阻系数温度相关部分为泥饼黏滞系数。由此可得

μr=μr1+K0+aT,

μs=μs1+Kf0+bT.

式中,μr和μs分别为旋转钻进和滑动钻进的摩阻系数;μr1和μs1为摩阻系数与温度无关的部分;K0和Kf0分别为0 ℃时的润滑系数和泥饼黏滞系数;a和b为公式系数。

将μr和μs替换原方程中的μ,并结合上文中热应力附加轴向力,得到考虑温度影响的摩阻扭矩计算模型。

4 钻井过程中井筒温度计算

要计算考虑温度影响的摩阻扭矩,需要先求得钻井循环时不同井深的温度:

Tp=C1eλ1z+C2eλ2z+Gz+Tmf-GB,

Ta=C1eλ1z(Bλ1+1)+C2eλ2z(Bλ2+1)+Gz+Tmf-BTfp.

式中,Tp和Ta分别为钻柱和环空中钻井液温度,℃;z为垂深,m;G为地温梯度,℃/m;Tmf为与压耗有关的参数,℃;C1、C2、λ1、λ2、B为方程系数,详细求解过程见参考文献[22]。

5 实例计算

根据建立的考虑温度影响的摩阻扭矩计算模型,对重庆涪陵焦石坝页岩气区块水平井X井进行摩阻扭矩计算分析。该井是一口水平生产井,钻进方式为复合钻进,井深4 518 m。三开水平段施工井眼直径为21.59 cm,使用实验中的油基钻井液钻进,钻具组合为:311.2 mmMD537+Φ216 mm×1.25°单弯螺杆+Φ285 mm扶正器+浮阀+Φ127 mm无磁承压钻杆+MWD组件+Φ127 mm加重钻杆×9根+Φ127 mm钻杆×171根+Φ127 mm加重钻杆×18根+Φ127 mm钻杆。按传统方法反演取套管段摩阻系数为0.15,裸眼段为0.25和0.3,地温梯度为3.1 ℃/100 m。

图8为不同井眼长度时钻杆内和环空中的循环温度剖面。

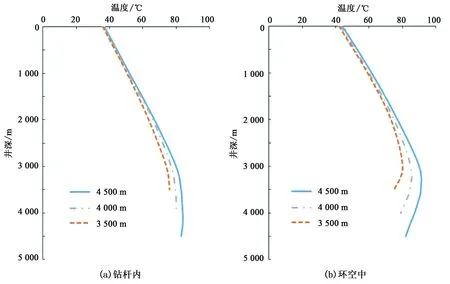
图8 不同井眼长度时钻杆内和环空中循环温度剖面Fig.8 Circulating temperature profile in drilling pipe and annulus at different well depth

按受温度影响的摩阻扭矩计算模型反演,计算出摩阻系数与温度无关的部分,得到旋转钻进摩阻系数公式为

μr[0]=0.12+0.000 7T,

μr[1]=0.198+0.000 7T.

滑动钻进摩阻系数公式为

μs[0]=0.12+0.000 2T,

μs[1]=0.198+0.000 2T.

其中，中括号内0和1分别指代套管段和裸眼段。

计算旋转钻进中的顶驱扭矩和滑动钻进中的大钩载荷,计算结果如图9、10所示,图中FF0和FF1分别指不考虑温度影响的模型中套管段和裸眼段摩阻系数。

将计算结果同现场实测值对比,用平均绝对误差分析计算精度。采用建立的受温度影响的摩阻扭矩计算模型,顶驱扭矩计算结果误差为3.7%。大钩载荷计算结果误差为4.4%,都具有较高的精度。

图9 旋转钻进顶驱扭矩计算结果Fig.9 Calculation results of top drive torque in rotary drilling

图10 滑动钻进大钩载荷计算结果Fig.10 Hook load calculation results of sliding drilling

6 结 论

(1)油基钻井液的润滑系数和泥饼黏滞系数都低于KCl聚合物润滑钻井液,在10～90 ℃,二者的润滑系数和泥饼黏滞系数都随温度增加而线性增加。

(2)从温度对钻井液润滑性和管柱热应力两方面考虑,建立受温度影响的摩阻扭矩计算模型。对涪陵页岩气焦石坝X井进行实例计算,考虑温度影响的计算模型所得顶驱扭矩随深度变化的趋势与现场实测值最为符合,其平均绝对误差为3.7%,大钩载荷的平均绝对误差为4.4%,皆优于未考虑温度影响的计算模型。

(3)考虑钻井循环温度影响的摩阻扭矩计算模型对钻井工程设计、水平井延伸极限预测等具有重要意义。