基于欧拉-拉格朗日方法的水下气体泄漏扩散行为研究

李新宏, 陈国明, 朱红卫, 畅元江

(中国石油大学(华东)海洋油气装备与安全技术研究中心,山东青岛 266580)

1 欧拉-拉格朗日数值建模方法

欧拉-欧拉和欧拉-拉格朗日方法可用于求解多相流动过程。欧拉-欧拉方法认为不同相是相互贯穿的介质,一相占有的体积不能被另一相占有,通过体积率来对计算域内不同相的分布情况进行描述。体积率是关于时间和空间的连续函数,不同相的体积率之和为1。VOF模型是一种在固定欧拉网格下的表面追踪方法,可以实现对多种不相容流体之间交界面的追踪。采用VOF模型对水和空气两相自由表面进行追踪,其连续性方程、动量方程和能量方程[13]分别为

(1)

ρg+F.

(2)

(3)

式中,aq为第q相体积分数;ρq为第q相密度,kg/m3;ρ为混合相密度,kg/m3;vq为第q相速度,m/s;Sh为源项;μ为湍流黏度和分子混合黏度总和,N·s/m2;g为自由落体加速度,m/s2;F为外部作用力,N;keff为热导率系数;T为温度,K。

将泄漏气体作为离散相处理,认为其是分布在连续流场中离散的气泡粒子。DPM是一种基于欧拉-拉格朗日方法的数值模型,采用DPM模型对海水中气泡粒子的运动轨道进行追踪,假设作为离散相的气泡粒子体积比率很低,分散粒子之间的相互作用以及粒子体积比率对连续相的影响均可忽略,在实际应用中要求离散相体积比率要小于10%～12%。

The old woman put the gingerbread man in the oven.Then she went to sleep in the chair.

DPM模型通过积分拉氏坐标系下的气泡粒子作用力的微分方程来求解离散相气泡粒子的运移轨迹,为每一个气泡粒子施加一个平衡力,使得离散相气泡粒子在扩散过程中,其运动惯性与所受其他外力达到平衡,气泡粒子受力平衡方程[2,13]为

(4)

(5)

Re=ρdp|up-u|/μ.

(6)

式中,u为流体相对速度,m/s;up为气泡粒子速度,m/s;FD为拖曳力,N;μ为流体动力黏度,Pa·s;ρ为连续相密度,kg/m3;ρp为气泡粒子密度,kg/m3;dp为气泡粒子直径,m;Re为相对雷诺数;CD为拖曳力系数,气泡受到拖曳力的大小取决于气泡的形状。计算拖曳力系数[14]为

(7)

式中,E0为表征气泡特征形状的无量纲Eotvos数。

E0表示为

(8)

式中,ρl和ρg分别为水和气体密度,kg/m3;σl为水的黏度,N·s/m2。

此外,泄漏气体的扩散过程属于复杂的非稳态湍流运动,气体从泄漏口喷射而出具有较高的雷诺数,选用Realizableκ-ε模型对气体扩散过程中的湍流特性进行描述,并使质量守恒、动量守恒和能量守恒的基本控制方程封闭[12]。

2 水下气体扩散仿真模型

2.1 网格模型

水下气体泄漏以后,气体从孔口喷射进入水中,在初始动能和浮力的作用下向水面方向扩散,整个泄漏扩散过程如图1所示。假定泄漏口所处水深为80 m,水面上部空气域高度为20 m,参考国际油气生产者协会(IOGP)发布的风险评估数据导则[12],取60 mm的泄漏孔径,建立三维几何模型,采用分块映射网格划分方法,对泄漏口以上中心区域的网格进行加密处理,以适应流场变化和保证求解精度。整个计算空间采用六面体网格,通过上述方法得到整个计算域的结构体网格模型如图2所示,网格总数为642 468个。

图2 网格模型Fig.2 Mesh model

2.2 边界条件

计算域顶部即空气域上部边界流体变量梯度为零,采用对称边界。计算域侧面和底部采用无滑移边界。泄漏口的初值条件在DPM模型中完成。气泡粒子从面射流源释放进入海流场中,气体密度变化服从理想状态方程,据Deepspill大尺度水下油气泄漏实验[15],气体在水下扩散过程中气泡尺寸分布如图3所示。通过UDF函数实现对气泡粒子密度与尺寸变化的控制。

选用非稳态压力基求解器,VOF模型启用隐式体力公式,部分平衡压力梯度和动量方程中的体积力,提高重力场中泄漏扩散模型的稳定性。PISO算法主要适用于非稳态问题求解,压力速度耦合采用PISO算法[12]。耦合求解过程中,采用随机轨道模型计入气泡粒子在湍流流场中扩散的附加拖曳力。

图3 气泡尺寸分布Fig.3 Bubbles size distribution

3 水下气体扩散模拟结果

3.1 数值模型验证

Engebretsen等[16]在挪威Statoil研究中心进行了小尺度的水下气体泄漏扩散实验,所用水池长9 m,宽6 m,高7 m。实验过程中使用空气作为介质,采用压力调节器维持恒定的气体泄漏速率,分别对泄漏速率为0.083、0.17和0.75 m3/s三种条件下的气体扩散行为进行实验研究。建立与实验同尺度的仿真模型,采用实验介质和泄漏速率,重复实验条件下的气体扩散过程,从而实现对数值模型的验证。图4为数值模拟与实验结果对比。从图4可以看出,3种泄漏速率条件下的气体上浮时间模拟值略高于实验值,但其差值较小。中心线速度的模拟值大于实验值,且随着距离泄漏源的高度增加,模拟值与实验值的差值减小,但模拟值与实验值的总体变化基本一致。因此,采用VOF和DPM耦合方法开展水下气体扩散行为研究是可行的。数值模型采用雷诺时均湍流模拟方法,其假设流场是完全发展的湍流,忽略分子间的黏性作用力,导致射流和羽流阶段的中心线速度的预测值高于实验值。此外,由于数值仿真是理想化的环境条件,难以和实验做到完全相符,模拟环境中海水对气体的阻力小于实验环境,从而导致模拟值与实验值存在一定偏差。

图4 仿真与实验结果对比Fig.4 Comparison of simulation results with experiment

图5为0.170 m3/s泄漏速率条件下气体水下运动轨迹和速度分布。据图5可知,水下气体泄漏后,气体向水面运动过程中,由于环境压力降低,其体积逐渐膨胀,扩散至海面形成一个倒立锥形的羽流结构。气体扩散过程中引起周围海水运动,计算域内速度分布形状与气体扩散轨迹较为一致,速度随着距离泄漏源高度的增加而减小,由羽流内层到外层逐渐减小。气体运动至水面时,带动表层水体运动,从中心迅速向周围扩展,在水面形成一个远大于水下羽流直径的水体波动区域。

图5 0.170 m3/s泄漏速率条件下气体扩散模拟结果Fig.5 Simulation result of underwater gas dispersion under release rate of 0.170 m3/s

3.2 水下气体羽流

泄漏口距离水面的距离为80 m,气体泄漏速率为50 kg/s,以此作为初值条件研究实例场景条件下的水下气体扩散行为。与大气环境相比,水中的压力和温度均随水深变化。因此,气体在水中运移扩散是一个复杂的过程。气体在水环境运移过程中,其密度变化服从理想气体状态方程,上升过程中密度逐渐减小。图6为水下气体羽流的发展过程。

图6 水下气体羽流发展过程Fig.6 Development of underwater gas plume

由图6可知,泄漏发生时,由于管道内的高压作用,泄漏气体以喷射状涌入水中,快速向上部空间发展。羽流上升过程中,环境压力逐渐降低,体积逐渐膨胀增大。当气体运动至水面时,气体与表层水相互作用,以溢出点为中心向四周拓展,形成倒立的锥形羽流结构。

图7为水下气体羽流垂向运动速度分布。由图7可知,泄漏初期,由于受到水的阻力速度急剧降低。泄漏后期,气体在水的浮力作用下,以近似恒定的速度,继续向水面扩散。图8为水下气体羽流几何尺寸变化过程。由图8可知,气体羽流垂向尺寸基本呈线性增长,泄漏时间为32 s时,气体扩散至水面。由于自由膨胀作用,气体向水面扩散的同时,逐渐向水平方向运动。据图8可知,由于受到相同的自由膨胀作用,气体羽流横向尺寸变化过程基本一致。

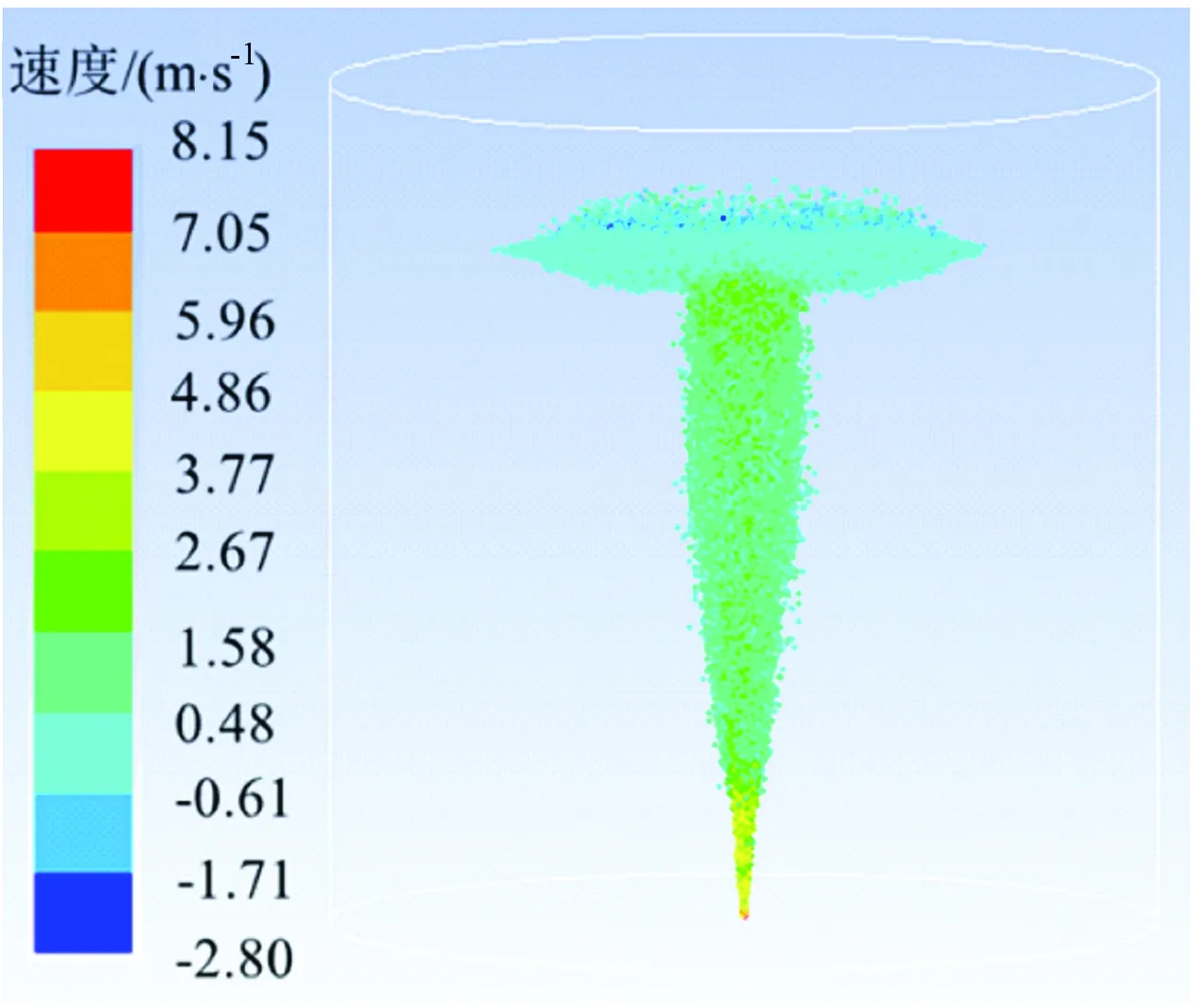
图7 气体运移速度分布Fig.7 Movement velocity distribution of underwater bubbles

图8 水下气体羽流几何尺寸Fig.8 Geometric sizes of underwater gas plume

3.3 水面涌流效应

气体运动至水面时,仍具有一定的速度,能够带动表层水运动,在水面溢出点附近形成沸腾效应,导致溢出点附近区域海水向上凸起,形成喷射水柱或涌流。溢出水面的气体如被引燃甚至可能造成严重的火灾或爆炸事故,该类事件已被工程实际所证实。2011年12月中海油珠海横琴天然气处理终端附近的海底输气管道发生泄漏[17],在该海域作业的渔民发现泄漏气体在海面形成的喷射水柱,后期运营方将泄漏天然气在海面做燃烧处理,形成10 m高的火焰高度,如图9所示。

图10为气体扩散至水面时空气-水相界面变化与相界面区域速度矢量分布。由图10可知,气体扩散至水面时引起溢出点处相界面凸起,即图9(a)中的涌流现象。气体运动至海面时,在溢出点区域形成沸腾效应,引起表层水回流,在溢出点区域两侧形成漩涡流动,并向溢出点两侧传递,该区域的速度矢量分布如图10(b)所示。

图9 珠海海底输气管线泄漏事故Fig.9 Leakage accident of subsea gas pipeline in Zhuhai

图11为水面气池中心涌流高度随时间的变化过程。气体扩散至水面时,沸腾效应引起的喷射水柱高度逐渐呈非线性和波动状增加。由图11可知,32～ 39 s之间喷射水柱高度迅速增加至3 m,由于表层水回流波动等因素,喷射水柱呈小幅度减小后,又逐渐增大。55 s时喷射水柱高度达到最大值4.4 m,55 s以后喷射水柱高度呈波动状发展。由图6可知,气体扩散至水面时,引起表层水运动,形成一个以气体溢出点为中心的圆形气池。图12为水面气池尺寸随时间的变化过程。由图12可知,随着气体的持续泄漏,气池半径逐渐增大,75 s时气池半径增大至42 m,75 s以后气池半径趋于稳定。

图11 气池中心涌流高度变化Fig.11 Variation of fountain height

图12 气体溢出区域尺寸变化Fig.12 Variation of radius of surface gas pool

4 结 论

(1)建立的三维水下气体扩散数值模型,实现了对水下气体扩散行为和水面涌流效应的预测和定量评估,仿真结果与小尺度实验数据对比论证了数值模型的可行性。

(2) 水下泄漏发生时,气体以喷射状涌入水中,在初始动能和浮力作用下向水面运动。由于环境压力降低,气体密度逐渐减小,体积膨胀增大,形成倒立锥形的羽流结构。气体扩散至海面时,带动表层水运动,引起羽流顶部两侧水回流,产生漩涡流动,在水面形成涌流效应。气体从水面溢出,引起表层水波动,以气体溢出点为中心向四周发展,在水面形成一个圆形的气池。水面涌流高度随时间呈非线性增长,达到峰值后呈小幅波动状变化,水面气池半径随时间逐渐增大后稳定。

(3)离散相与连续相耦合的方法能够有效用于水下气体泄漏扩散精细分析,确定水下气体运移轨迹、上浮时间、水面涌流高度和气池尺寸等重要参数,对水下气体泄漏事件风险评估和应急决策具有较好的参考价值,从而提高风险防控与事故处置的科学性与合理性。