半潜式海洋平台输出反馈终端滑模动力定位系统
赵东亚, 高守礼, 梁 浩, 赵 通
(中国石油大学(华东)化学工程学院,山东青岛 266580)
动力定位(dynamic positioning,DP)技术是利用主动推进器来克服环境因素如风、浪、流等干扰,保持海洋平台的位置和航向,最终实现平台以固定的位姿状态保持在海面某一位置或精确地跟踪某一给定轨迹。在海上钻井平台、机器人研究、科学考察等领域有广泛应用[1-2]。由于在大多数情况下海上钻井平台的速度很难测量,根据噪声污染的位置和航向信号设计状态观测器估计速度信号具有实际意义。基于状态观测器的输出反馈控制器设计是海洋平台动力定位控制的关键问题。最初的动力定位系统采用传统的PID控制器,通过低通或陷波滤波器级联抑制误差产生。从20世纪70年代中期,基于最优控制和卡尔曼滤波器理论,Balchenetal等[3]提出了先进控制的概念。Fossen等[4-5]使用反步法进行非线性观测器设计,并应用于船舶动力定位的输出反馈控制。Balchen等[6]提出改进的LQG控制算法,后被扩展到基于模型的控制器设计,能够实现定点和轨迹追踪控制[7]。Tannuri等[8-9]将滑模控制理论应用于欠驱动船舶动力定位系统轨迹跟踪控制,并通过实验进行验证。Ashrafiuon等[10]进行实验分析,验证了动力定位系统滑模控制的有效性和优越性。Kim等[11]针对船舶动力定位控制,提出了鲁棒非线性观测器。杜佳璐等[12-14]应用串级理论设计了一种高增益观测器-控制器设计方案,能够实现船舶动力定位的输出反馈控制。然而这些方法均为渐近稳定,需要高增益以增加控制系统收敛速度和系统鲁棒性,高增益控制往往会引起控制器输出饱和。滑模观测器自身具备很强的鲁棒特性,对系统不确定性和外部环境干扰具有较强的抑制能力,对低频信号进行估计,对高频信号进行滤波,可实现对半潜式海洋平台状态的有限时间估计[15-16]。笔者提出一种基于滑模观测器的输出反馈终端滑模控制的设计方法,可实现海洋平台的有限时间的观测与稳定控制,获得较快的收敛速度和较强的鲁棒性,同时避免控制器饱和。
1 问题描述
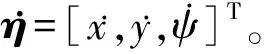
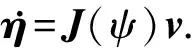
(1)
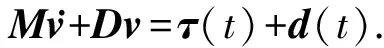
(2)
其中
τ∈R3×1.
式中,J(ψ)为雅可比矩阵;M,D∈R3×3分别代表惯性矩阵和线性阻尼矩阵;τ和R分别为纵荡、横荡方向的控制力及艏摇方向的控制力矩;d∈R3×1为风、浪、流干扰及未建模动力学特性。
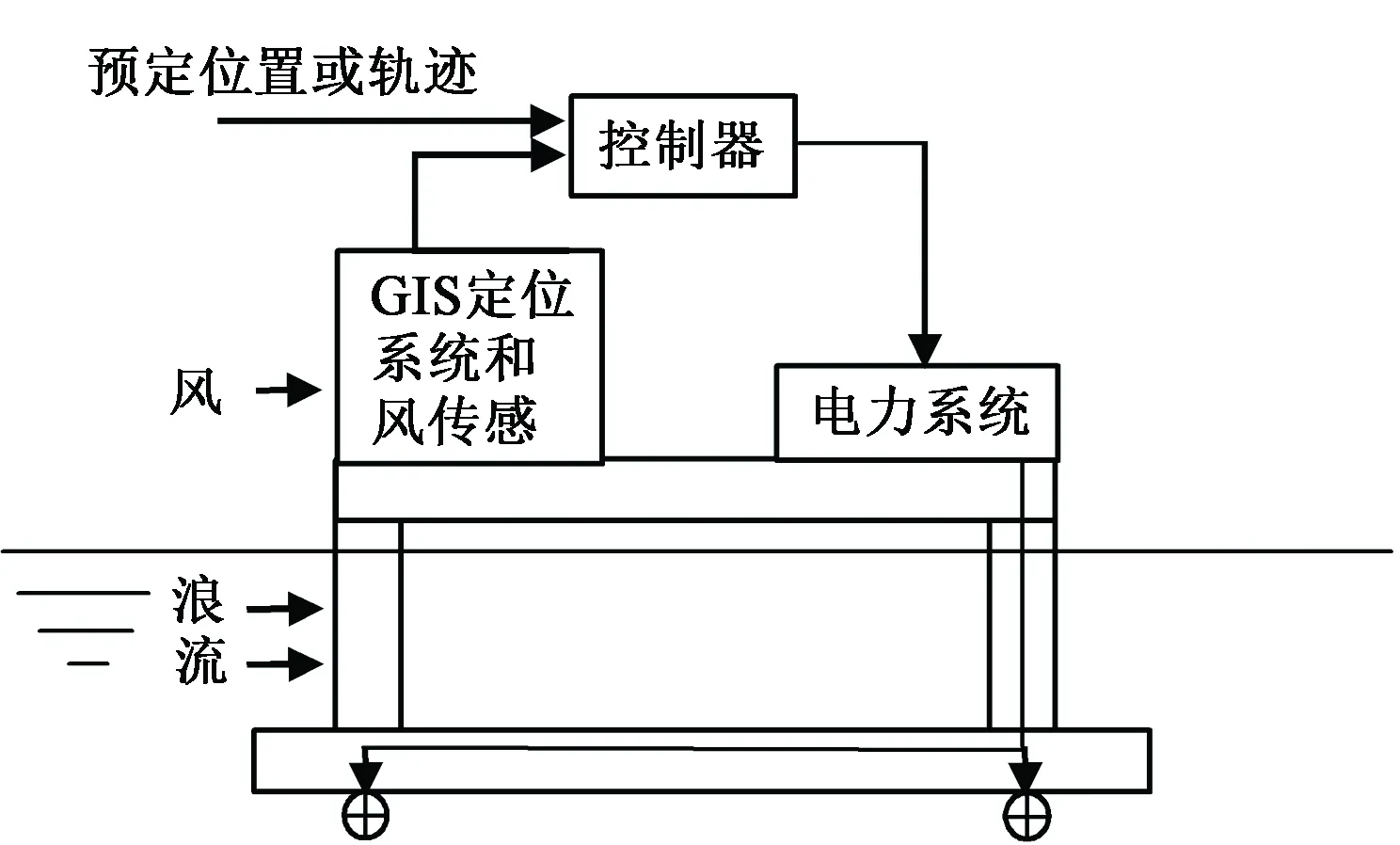
图1 半潜式海洋钻井平台动力定位系统Fig.1 Dynamic positioning system of semi-submersible offshore drilling platform
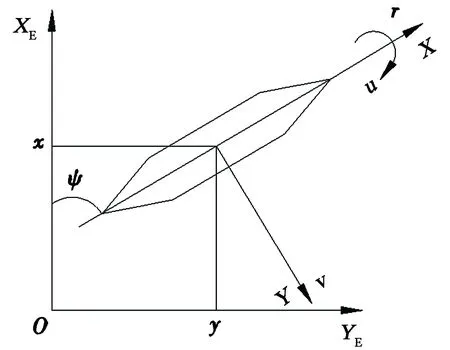
图2 平台地球坐标系和平台坐标系Fig.2 Earth coordinate system and platform coordinate system
假设d有界,满足
‖d(t)‖
(3)
式中,d0为干扰和不确定性的上界。
平台的横摇与纵摇运动均是零均值且振幅有限。通常的平台都是稳心稳定的,这意味着在摇晃和倾斜中存在恢复力矩。假设平台足够稳心稳定,雅可比矩阵可用于描述运动方程,即

(4)
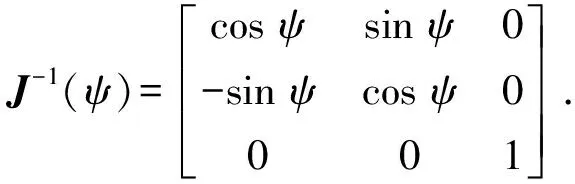
(5)
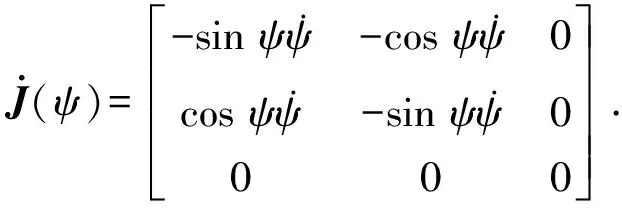
(6)
J(ψ)对于所有ψ均是非奇异的。
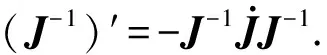
(7)
由式(1)可知,v可以表示为
(8)
对式(8)进行求导,可得
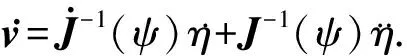
(9)
联立式(2)和(9),整理得到
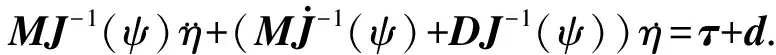
(10)
为了对式(10)进行简化,令
P(η)=MJ-1(ψ),
式(10)可以简化为
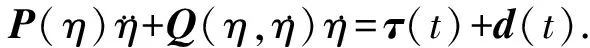
(11)
2 滑模观测器设计及稳定性证明
由式(11)可得
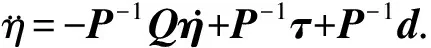
(12)
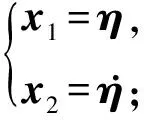
则x1=η,
其中
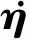
假设1:d代表外部干扰,且有‖d‖≤d0,d0>0为正常数,即d有界。
假设2:因为M可逆、J可逆,那么P=MJ-1可逆。
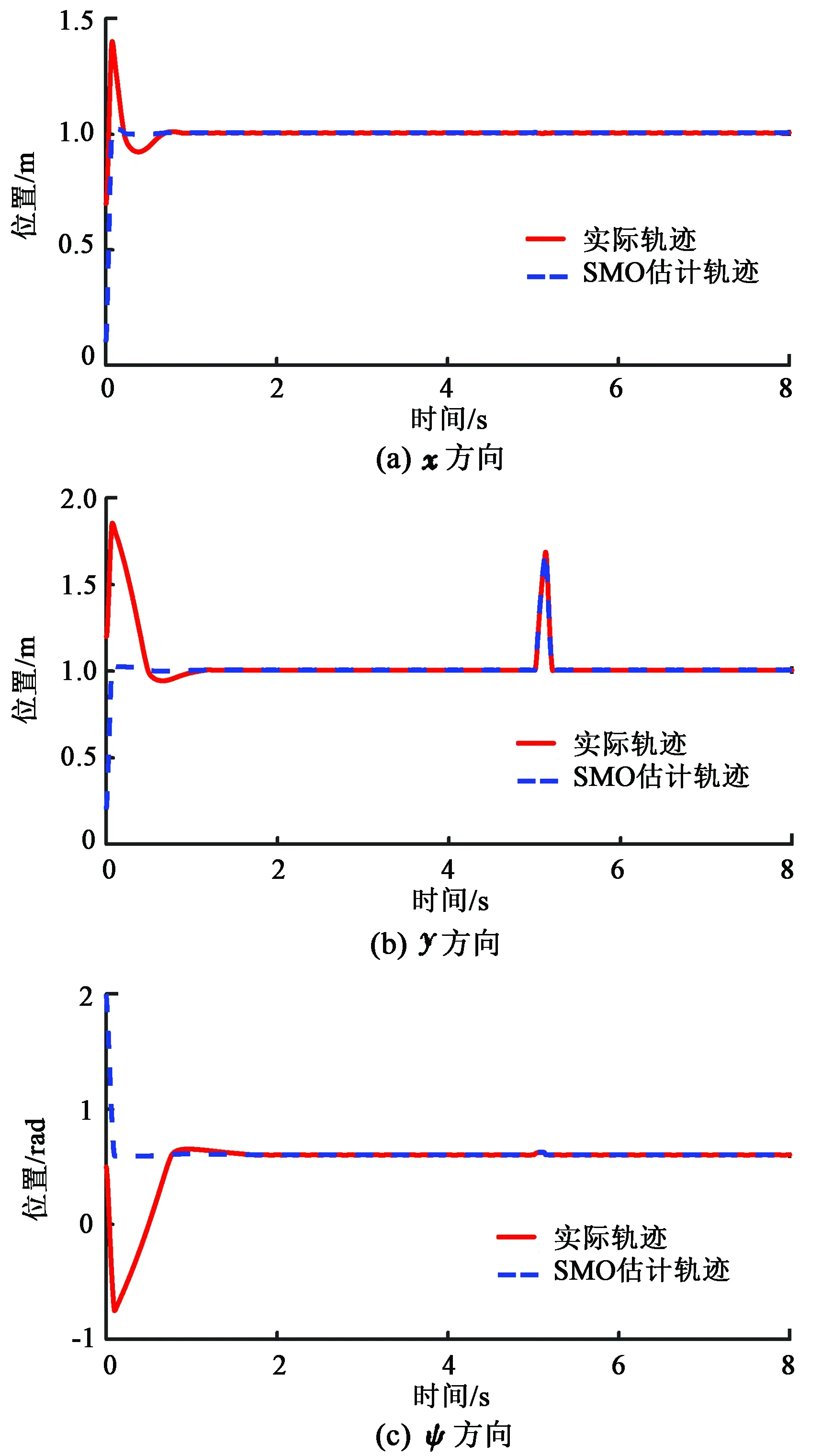
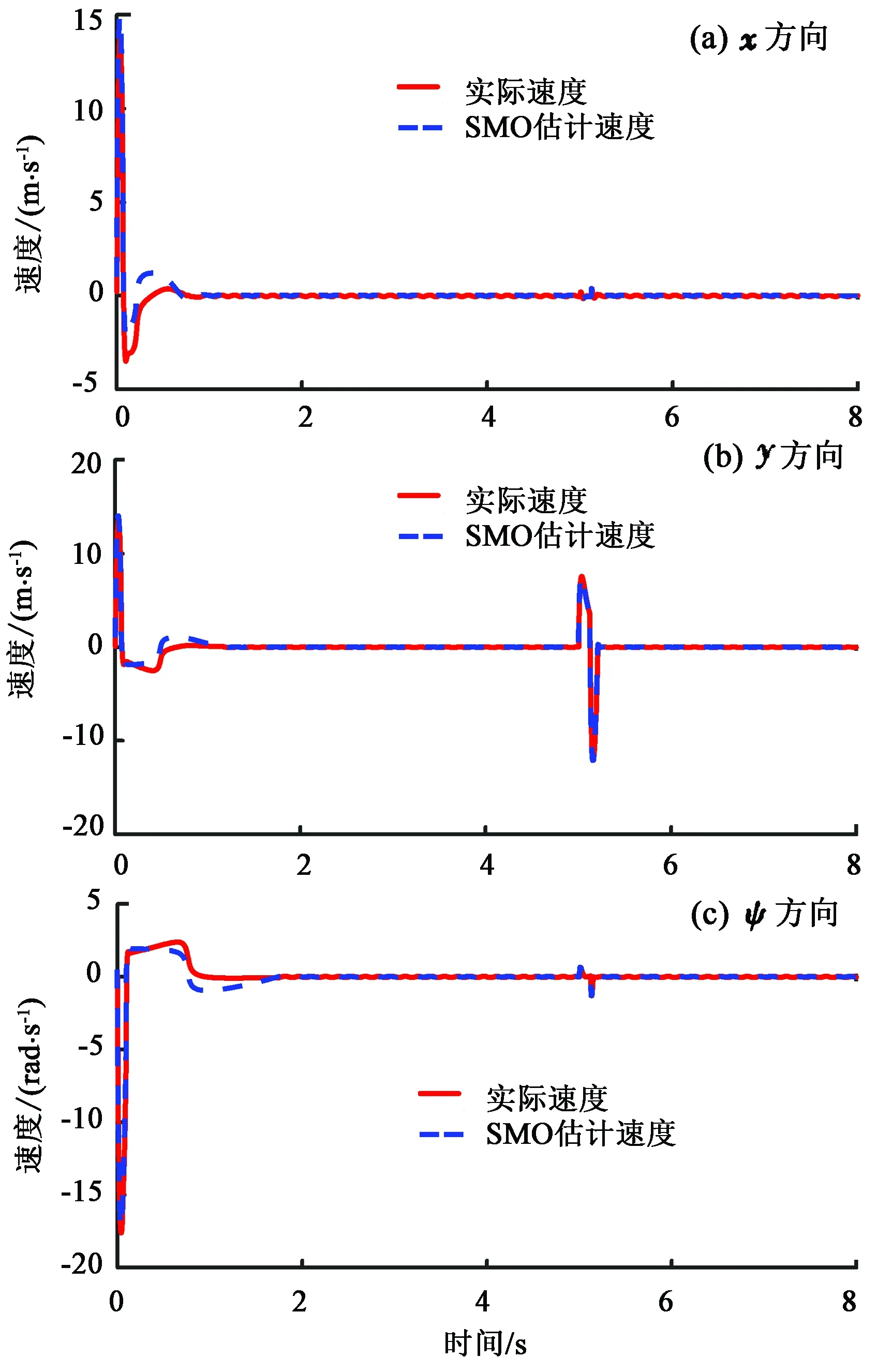
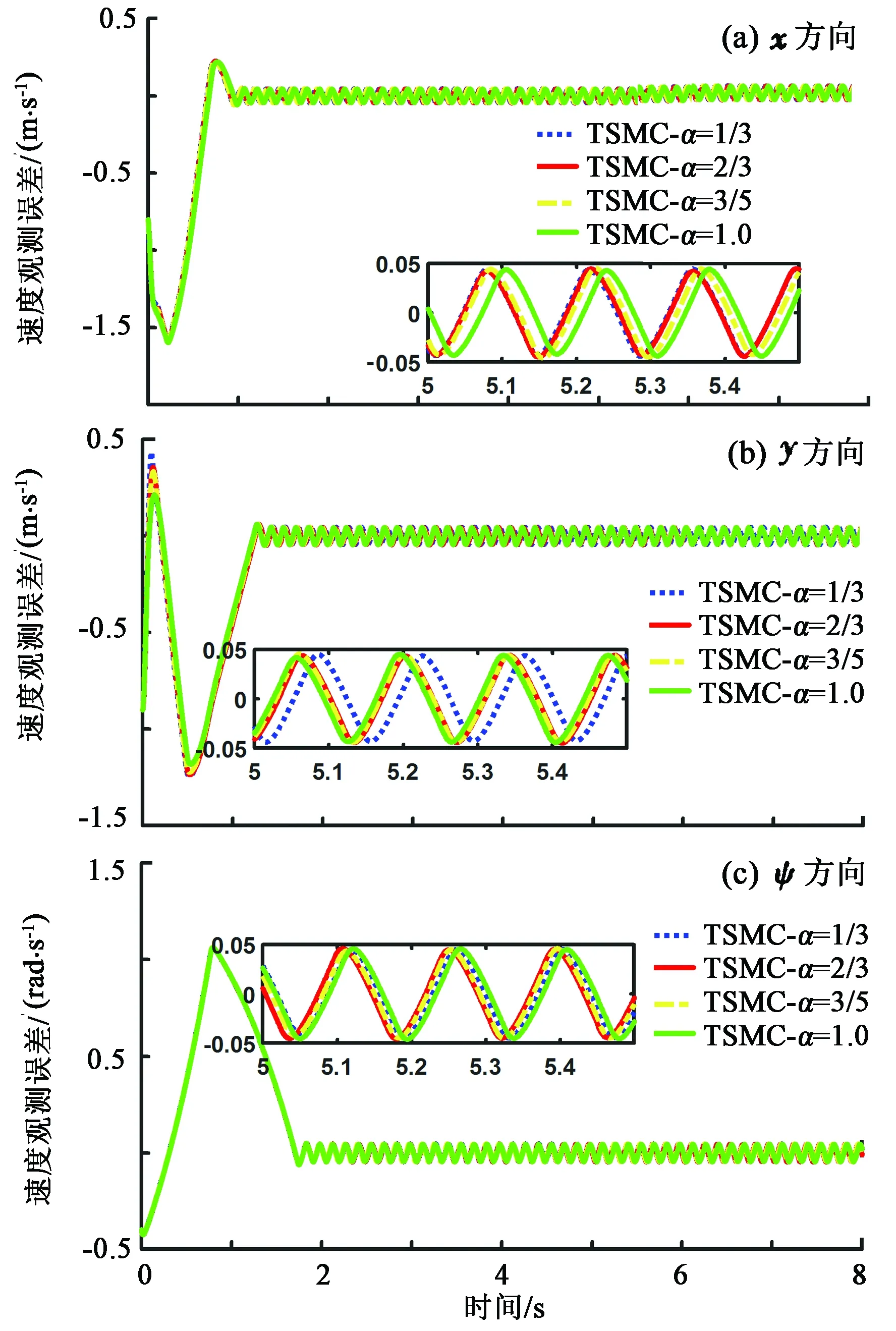
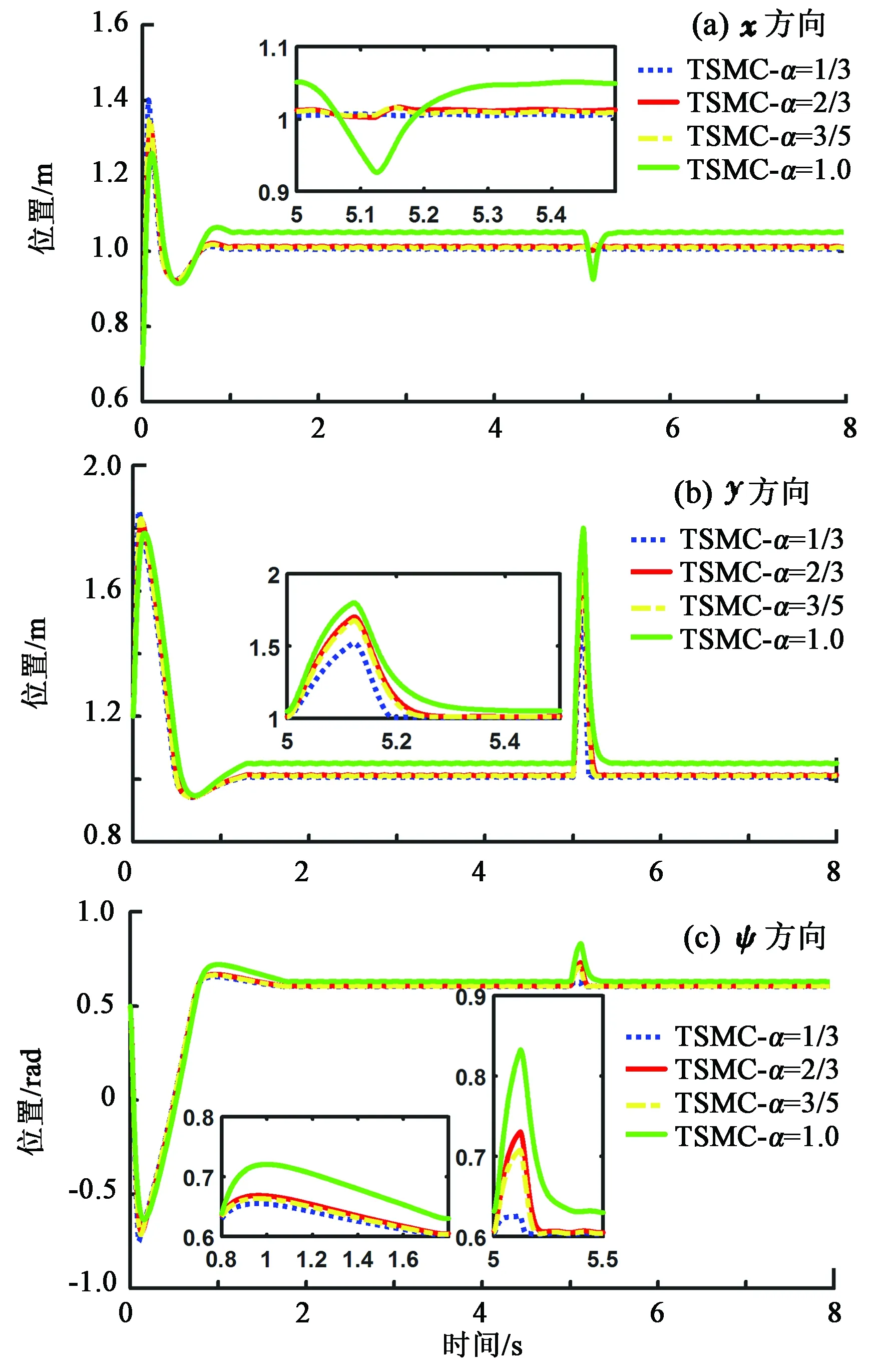
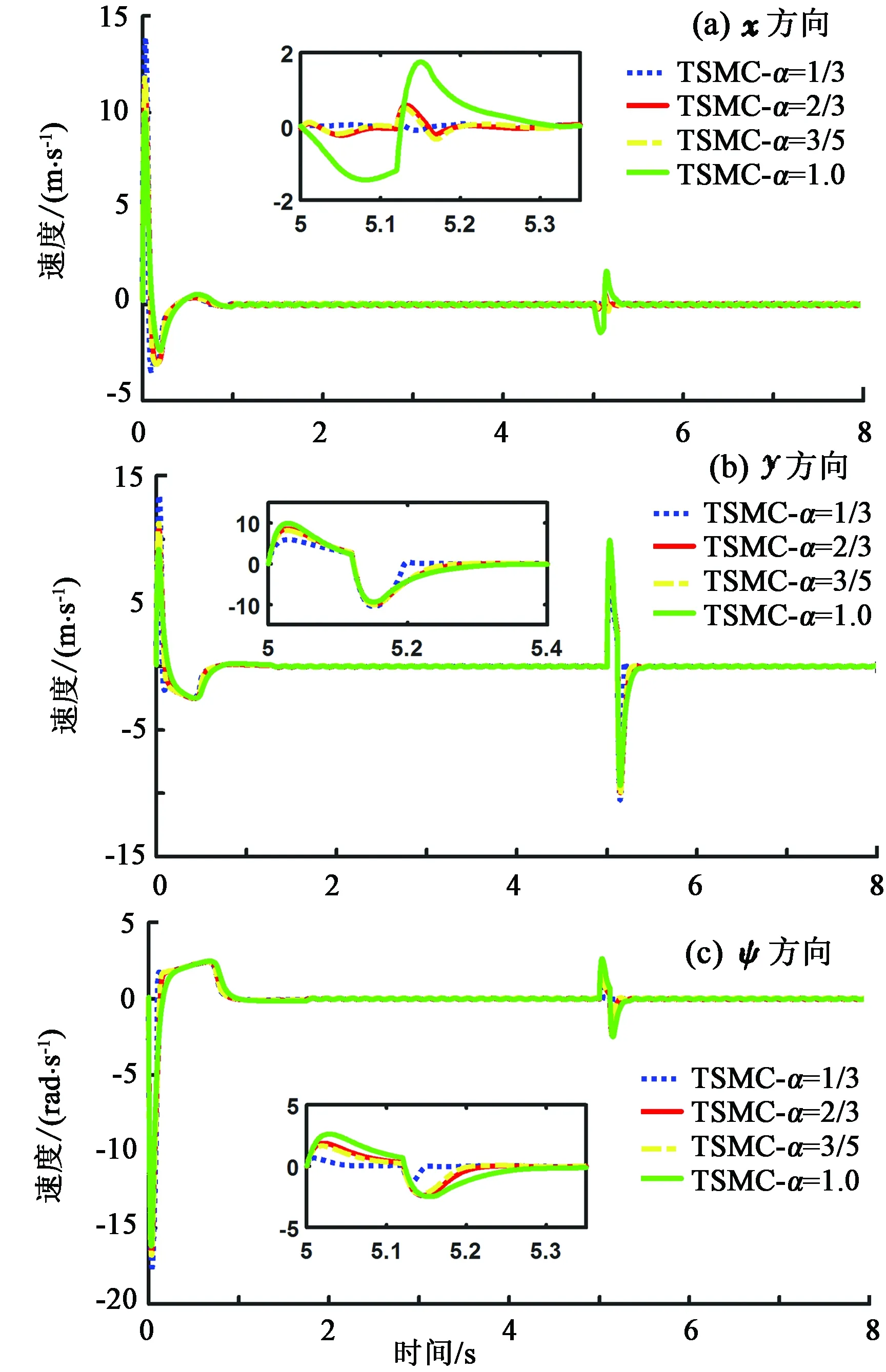
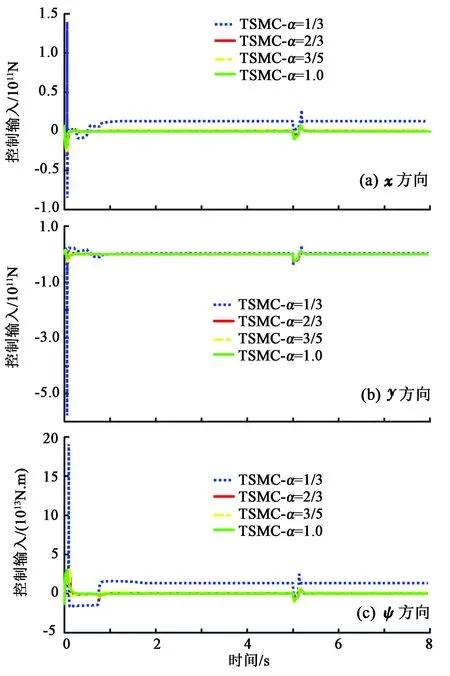
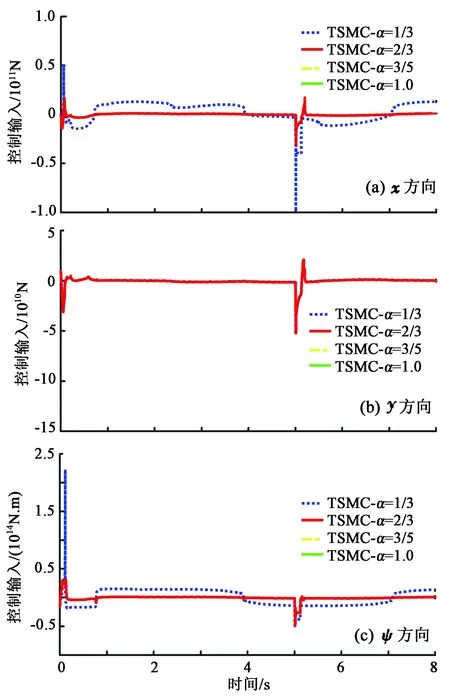
假设3:系统状态x2有界,即‖x2‖≤r,0 式(12)系统的状态方程和输出方程为 (13) 设计滑模观测器为 (14) 其中 令 则由式(13)和(14)做差可得观测误差为 (15) 其中 证明:(1)选取第一个Lyapunov函数。 (16) 对时间求导数可得 (17) (18) 选取第二个Lyapunov函数: (19) (20) (21) (22) (23) (24) 定义系统的误差信号e及其微分为 (25) 其中 式中,xd、yd、ψd分别为纵荡、横荡、艏摇方向的期望值。 跟踪误差及其微分的估计值为 (26) 设计估计滑模函数为 (27) 其中 一般情况下,p2是正奇数且满足条件: (28) 终端滑模控制律τ(t)设计为 τ(t)=τ0+τ1. (29) 其中 式中,μ和ξ均为控制器参数。 为了实现有限时间稳定,设计了不连续的控制律τ1,然而,不连续的控制可能会产生较大的抖振。为了避免抖振,采用边界层方法代替不连续控制,新的控制律τ1可以重新设计为 (30) 式中,δ为所取边界层。 证明:选取Lyapunov函数为 (31) (32) 代入τ0可得 (33) 代入τ1可得 (34) (35) 其中 为验证所设计输出反馈终端滑模控制器的有效性,以某半潜式海洋平台为研究对象,对定位过程进行仿真研究。该控制对象参数来源于文献[20]和[21],其质量矩阵和阻尼矩阵分别为 (36) (37) 海洋钻井平台的动力定位系统工作时,来自海上复杂环境风、浪、流的干扰集中在一起发生作用,仿真研究中包括与真实工况一致的高频(high frequency)干扰和低频(low frequency)干扰。研究两种情况:一种是基于滑模观测器的设定点跟踪控制,另一种是基于滑模观测器的期望轨迹跟踪控制。在这两种情况下,基于干扰和未建模特性的假设下将分别测试TSMC和SMC控制算法。 外界环境干扰和集中不确定性d为 (38) (39) 图3、4给出了α=1/3时滑模观测器对3个方向上位置和速度状态估计追踪曲线。由图可知,在较短时间内观测器状态估计信号能追踪并保持在实际信号上。当脉冲干扰f发生时,观测器也能迅速跟踪到系统的实际状态。 图3 滑模观测器(x,y,ψ) 方向上位置估计Fig.3 Position estimation curves of sliding mode observer in (x,y,ψ) direction 图4 滑模观测器(x,y,ψ) 方向上速度估计Fig.4 Velocity estimation curves of sliding mode observer in (x,y,ψ) direction 图5为滑模观测器位置信号观测误差曲线。由图5可知,观测系统迅速响应,在t≈1 s,位置状态估计信号能追踪并保持到实际位置上,各方向观测误差均被限定在[-10-3,10-3]内,对位置信号状态估计效果很好。图6为滑模观测器速度信号观测误差曲线。由图6可知,观测系统迅速响应,在t≈1.7 s,速度状态估计信号能到达并保持到实际速度上,各方向观测误差均被限定在[-0.05,0.05]内,对速度信号状态估计效果很好。 图5 滑模观测器位置信号观测误差Fig.5 Observation error curve of sliding mode observer position signal 图6 滑模观测器速度信号观测误差Fig.6 Observation error curve of sliding mode observer velocity signal 图7 滑模控制器定点位置追踪Fig.7 Position tracking of sliding mode controller for fixed point 图8 滑模控制器定点速度追踪Fig.8 Velocity tracking of sliding mode controller for fixed point 图9分别为纵荡、横荡方向的控制力和艏摇方向的控制力矩曲线。采用边界层方法使得各控制力矩均光滑且有界。当α=1时初始有严重超调现象。 图9 滑模控制器定点控制输入Fig.9 Input curve of sliding mode controller for fixed point tracking 为了简化问题,仅给出滑模控制器的性能曲线。仿真结果如图10~13所示。 图10 x方向轨迹位置追踪Fig.10 Position tracking for trajectory tracking in x direction 图12 滑模控制器轨迹速度追踪Fig.12 Velocity tracking of sliding mode controller for trajectory tracking 图13 滑模控制器轨迹控制输入Fig.13 Input curve of sliding mode controller for trajectory tracking (1)提出的新输出反馈终端滑模控制器设计方法中充分考虑了外部环境因素如风、浪、流等干扰及未建模特性的影响,所设计滑模观测器能够提供船舶速度估计,并提供高频波频运动的滤波。 (2)利用非线性观测器对非线性干扰进行处理是必要的,与高增益观测器相比,可以避免输出饱和情况。 (3)基于滑模理论设计的输出反馈终端滑模控制器能够保证系统闭环稳定,收敛到期望值附近。 (4)随着终端滑模指数项α增大,控制系统性能呈现逐渐变差的趋势,而且系统鲁棒性有所下降,控制力矩也随之增大。MATLAB仿真验证了所设计的输出反馈终端滑模控制器,能够实现半潜式海洋平台精准的动力定位和轨迹追踪控制,具备较强的抵抗外界干扰的能力。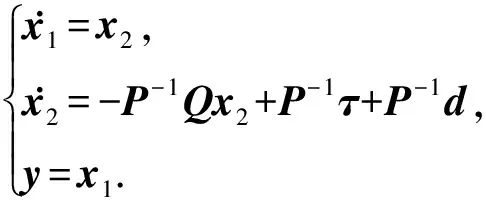
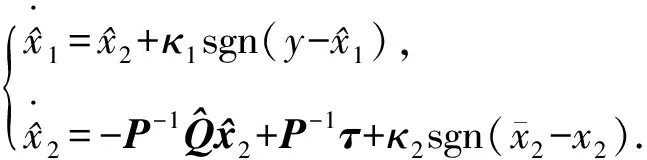
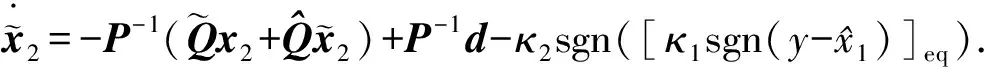
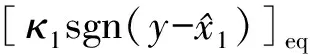
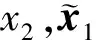
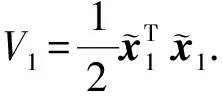
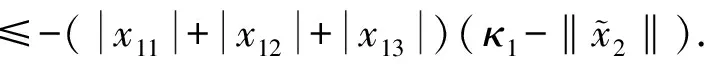
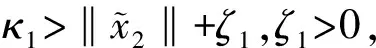
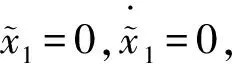
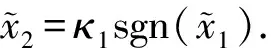




3 输出反馈终端滑模控制器设计
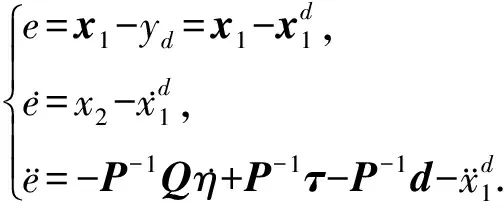
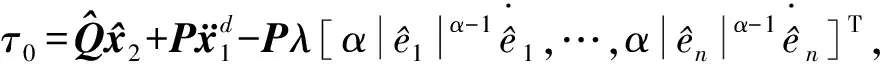
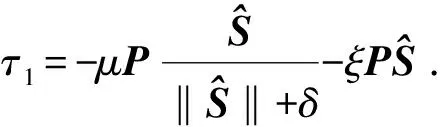
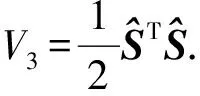


4 仿真验证及分析
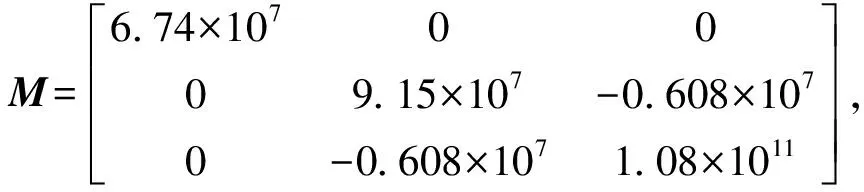

4.1 定位控制
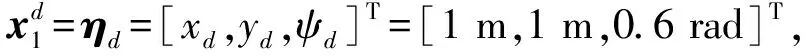

4.2 轨迹跟踪控制
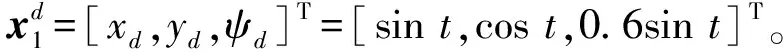


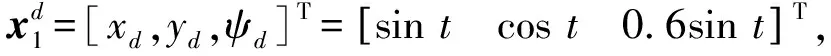
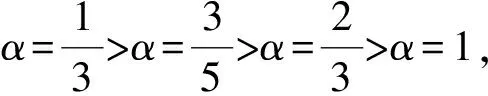
5 结 论

