基于能量理论的体积压裂工程改造效果评价模型及应用

冯福平, 黄 芮, 雷 扬, GUO Boyun, 胡超洋, 王胡振

(1.东北石油大学提高油气采收率教育部重点实验室,黑龙江大庆 163318; 2.中国石油天然气集团有限公司油气藏改造试井与评价重点研究室,黑龙江大庆 163318; 3.University of Louisiana at Lafayette, Lafayette 70506, USA)

体积压裂技术能够形成复杂的裂缝网络[1-3],极大地提高储层的整体渗透率[4-5]。体积压裂工程改造效果通常采用微地震监测数据得到的储层改造体积(stimulated reservoir volume,SRV)评价[6-8],Fisher、Maxwell等[9-11]指出在Barnett页岩气井中SRV与产能具有良好的相关性,但是在致密油中这一关系并不明显[12-13];Guang Zhao[14]、Guang Yu[15]、翁定为[16]、Nassir[17]等建立了储层改造体积计算模型,Cipolla[6]提出采用裂缝复杂性指数(fracture complexity index,FCI)表征体积压裂的效果,但这些方法均不能反映改造范围内裂缝的密度以及导流能力。笔者根据能量守恒和物质平衡原理,通过变分法建立改造体积内平均裂缝长度和等效裂缝条数计算模型,综合考虑影响体积压裂工程改造效果的改造体积、裂缝密度以及导流能力这3大因素,提出有微地震监测井和无微地震监测井的体积压裂工程改造效果评价模型,实现体积压裂工程改造效果的准确评价,为压裂设计优化、油气井产能预测和井间产能差异分析提供基本的依据。

1 体积压裂工程改造效果影响因素

常规压裂一般形成双翼对称裂缝,用来表征其压裂工程改造效果的评价参数通常为裂缝半长和导流能力。体积压裂会形成复杂的立体裂缝网络,裂缝半长及导流能力已不能合理地反映其压裂工程改造效果。体积压裂油气井的产能主要取决于改造体积及其等效渗透率,因此其工程压裂效果主要受储层改造体积以及反映其等效渗透率的缝网内裂缝密度和导流能力的影响。通常情况下,较大的储层改造体积以及内部较高的裂缝密度和导流能力能够取得相对较好的产能,这种情况下体积压裂的工程改造效果最好。

1.1 储层改造体积的影响

储层改造体积通常由微地震事件所包含的体积SRV表示。一般情况下SRV与油气井产能之间存在正相关关系[18],SRV越大说明压裂效果越好。但是SRV与压裂工程改造效果和油气井产能之间的关系并不是绝对的,在某些情况下SRV可能与油气井产能之间存在负相关性,无法准确合理地进行压裂工程改造效果评价以及解释和区分油气井间产能差异的原因,容易造成误判现象。其原因在于:① 微地震监测得到的SRV包含了压裂过程中产生的所有微地震事件区域,但是并不是所有的微地震事件都代表着裂缝的启裂或扩展。有些微地震事件是由于发生在裂缝网络外部的剪切滑移事件造成的,这种情况下产生的裂缝并未与主裂缝沟通,部分裂缝虽然与主裂缝沟通但由于应力条件的限制压裂液和支撑剂并未进入其中,在没有支撑剂的条件下,这部分改造体积对油气井产能的贡献较小,因此微地震事件反映的SRV与对油气井产能起主要贡献的真实储层改造体积并不一致,通常情况下微地震事件得到的SRV都要大于真实储层改造体积[19-23],但是由于微地震监测技术自身的缺陷以及地质条件的复杂性,微地震事件得到的SRV与真实储层改造体积之间的关系目前还无法得知;②油气井产能并不仅仅依赖于SRV的大小,SRV内裂缝的密度以及导流能力对油气井产能同样具有重要的作用。虽然微地震数据能够反映储层改造区域的大体形状和位置,但其不能提供改造体积内部裂缝的详细结构以及支撑剂的分布[18,24]。由于SRV内裂缝的密度以及导流能力不能通过微地震数据反映,因此体积压裂工程改造效果不能仅依靠SRV评价。

1.2 缝网内裂缝密度的影响

体积压裂改造体积内裂缝密度越大(条数越多,间距越小)说明裂缝网络越复杂,基质中的流体向裂缝的渗流距离越短,油气井产能和最终采收率就越高,压裂工程改造效果就越好[25-26]。Mayerhofer 等[27]研究表明,在考虑缝间干扰的条件下,缝间距一般应选择小于30 m。

1.3 裂缝网络导流能力的影响

体积压裂的主要目的就是在储层中形成缝网状的具有高导流能力的渗流通道,从而降低油气从地层中流向井眼的阻力。压裂过程中需要将大量的支撑剂泵入地层,使裂缝在储层闭合应力的作用下仍能保持部分张开状态并提供较高的导流能力,支撑剂的长期导流能力直接决定着压裂工程改造效果以及油气井的长期产能。在支撑剂的种类、粒径、嵌入铺置方式、地层闭合应力等不变的情况下,缝网的导流能力主要受支撑剂浓度的影响,单位裂缝面内较多的支撑剂将会显著提高缝网的导流能力,在同等条件下注入地层中的支撑剂越多压裂改造后油气井的产能就越高[28],体积压裂的工程改造效果就越好。因此可以用支撑剂的浓度表征裂缝的导流能力,Fredd等[29]进行了详细的不同支撑剂浓度条件下的裂缝导流能力测试实验,可以作为体积压裂缝网导流能力确定的基本依据。

2 改造体积内平均裂缝长度和等效裂缝条数计算模型

体积压裂工程改造效果受到SRV及其内部裂缝密度和导流能力的共同影响,其中SRV可以通过微地震监测数据获得;改造体积内裂缝的密度可以用裂缝的条数表示;裂缝网络导流能力可以由裂缝内支撑剂的浓度分布表征,压裂过程中注入地层中的支撑剂体积已知,其关键是获取SRV内裂缝的总支撑长度。因此要想能够准确地进行体积压裂工程改造效果评价,须知道改造体积内的裂缝总长度以及裂缝的条数,用来表征改造体积内的裂缝密度和导流能力。

体积压裂过程中人工裂缝首先沿着原地最大水平地应力方向扩展,在其扩展过程中由于天然裂缝、诱导应力、岩石力学性质的影响会产生各级分支裂缝甚至是主裂缝偏转,因此体积压裂形成的裂缝网络不可能是形状规则的缝网。由于地质条件和应力分布的复杂性,无法得出这些裂缝的条数、各自的位置以及长度。众多研究者分别建立了多种2维和3维体积压裂裂缝网络模型[30-39],但这些模型的应用具有一定的限制:一部分模型需要人为设定裂缝的条数或间距,各条裂缝之间相互平行或正交,不符合实际压裂过程中受应力和地质条件共同控制的裂缝网络的复杂性和不规则特征;另一部分模型虽然能够模拟出不规则的缝网形状,但是需要对天然裂缝的分布有准确的认识,而这些模拟所用的天然裂缝网络(包括位置、倾向、尺寸等)都是研究者自己假定的,与实际天然裂缝的分布有较大的差别,因此要准确模拟体积压裂改造体积内裂缝的条数及分布非常困难。由于水力压裂过程是依靠高压流体在地层岩石中创造裂缝的过程,这一过程将会遵守能量守恒和物质平衡原理,可以根据水力压裂过程中遵循的这些原理分析裂缝网络内多条裂缝的平均长度和等效裂缝条数,将缝网内大小、位置分布及形状复杂的各级裂缝进行等效,实现体积压裂改造体积内缝网密度和长度的等效描述。

在分析之前,为了将问题进行简化,假设:储层岩石横观各向同性;岩石变形属于弹性变形(不考虑塑性变形);各条裂缝的形状在截面上为矩形(各点缝宽相同);裂缝网络内各条裂缝具有相同的缝高;每一条裂缝的长度为裂缝网络内多条裂缝的平均长度,平均裂缝长度与等效裂缝条数的乘积为改造体积内裂缝的总长度。

2.1 体积压裂过程中的能量守恒原理

水力压裂裂缝的形成是一个能量转换的过程,这一过程要遵循能量守恒原理。

体积压裂过程中注入地层中的能量[2]为

Einj=pinjqinjt.

(1)

式中,Einj为注入地层中的能量,J;pinj为缝口注入压力,Pa;qinj为注入排量,m3/s;t为注入时间,s。

体积压裂过程中注入地层中的总能量转化为以下几项:裂缝内流体的压力能;裂缝内流体的动能;裂缝张开形成的岩石弹性变形能;岩石张开形成的表面能;裂缝内流体流动消耗的摩擦能;裂缝内流体滤失消耗的压力能。其中裂缝内流体具有的压力能为

Ep=pV=pnwhx.

(2)

式中,Ep为裂缝流体具有的压力能,J;p为裂缝内的平均压力,Pa;V为裂缝的总体积,m3;n为等效裂缝条数;w为缝宽,m;h为缝高,m;x为裂缝的平均长度,m。

裂缝内流体具有的动能为

(3)

式中,Ek为裂缝内流体具有的动能,J;m为裂缝内流体的质量,kg;v为裂缝内流体的速度,m/s;ρ为流体的密度,kg/m3。

裂缝张开形成的岩石弹性变形能为

(4)

式中,Ee为弹性变形能,J;σ为应力,Pa;ε为应变;Vr为岩石变形的体积, m3;σn为裂缝流体的净压力,Pa;σh为最小水平地应力,Pa。

岩石张开形成的表面能为

Es=2esnhx.

(5)

式中,Es为表面能,J;es为比表面能,J/m2。

裂缝内流体流动消耗的摩擦能为

(6)

式中,Ef为流体流动消耗的摩擦能,J;f为范宁摩阻系数;A为裂缝的横截面积,m2。

裂缝内流体滤失消耗的压力能为

El=pVl.

(7)

其中压裂液的滤失体积表达式为

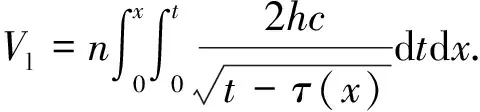
(8)

则压裂过程中的能量守恒方程可以表示为

Einj=Ep+Ek+Ee+Es+Ef+El.

(9)

2.2 最小能量路径的变分法原理

根据哈密顿原理,体积压裂过程中的拉格朗日函数可以表示为

L=(Ep+Ek)-(Ee+Es+Ef+El).

(10)

裂缝内的压力能和流体动能向岩石的弹性变形能、表面能以及流体流动摩擦能的转化遵循最小能量路径,由变分法原理可知拉格朗日函数L应满足的平衡方程为

(11)

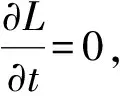
(12)

式中,C为积分常数,可由边界条件求得。

2.3 平均裂缝长度及等效裂缝条数计算模型

将式(2)～(7)及(10)代入式(12)中,整理后可得到:

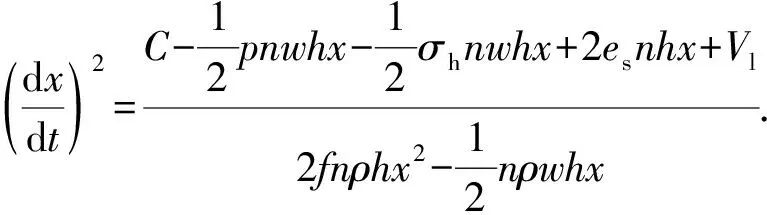
(13)

压裂过程中的物质平衡方程为

(14)

将式(13)和(14)代入式(9)中,可以得出任意时刻平均裂缝长度的表达式为

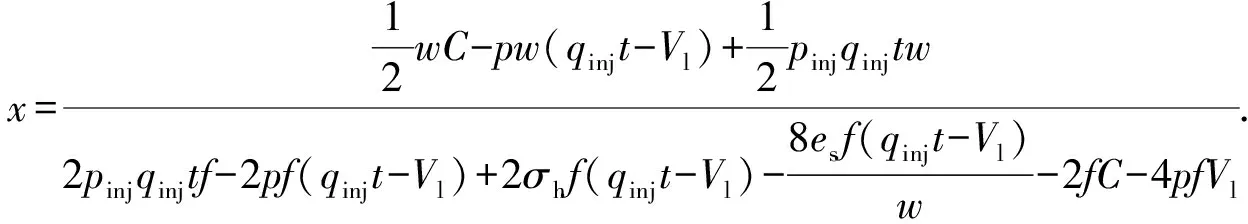
(15)

其中裂缝的平均宽度计算式为

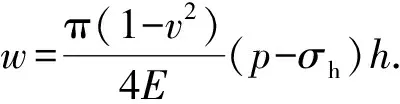
(16)

式中,v为泊松比;E为弹性模量,Pa。

压裂过程中裂缝的扩展速度为此时裂缝内流体的流动速度,在压裂的初始时刻(t=0时),裂缝的扩展速度等于此时孔眼内流体的流动速度,由此边界条件即可求出常数C的取值。由式(15)可以得出初始时刻裂缝的扩展速度为

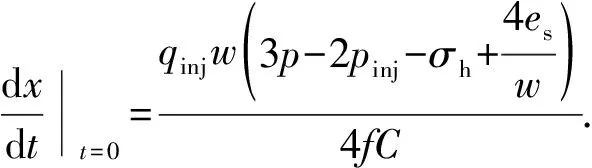
(17)

此时孔眼内的流体流动速度为

(18)

式中,N为射孔孔眼个数;r为孔眼半径,m。

根据初始时刻裂缝的扩展速度等于此时孔眼内液体的流动速度这一边界条件,由式(17)和(18)可以得出常数C的表达式为

(19)

将式(15)代入式(14),可以得出改造体积内等效裂缝条数的表达式为

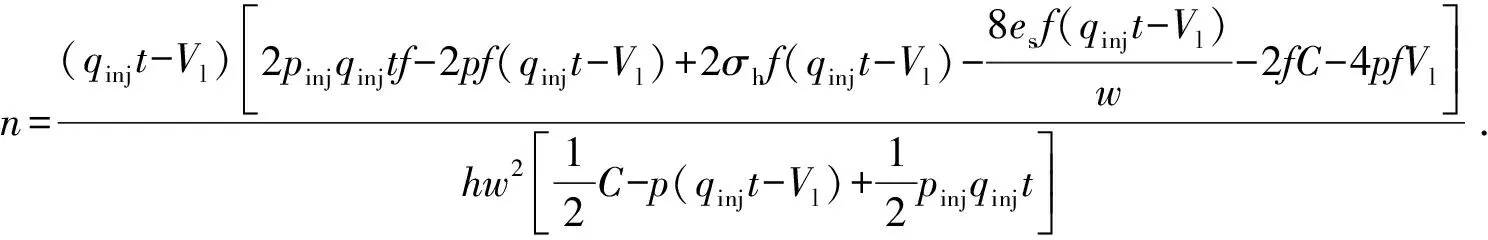
(20)

在压裂过程的任一时刻,改造体积内的平均裂缝长度和等效裂缝条数可以通过式(15)、(20)联立式(16)、(19)求得。

2.4 改造体积内平均裂缝长度和等效裂缝条数求解方法及流程

由式(15)和(20)可以看出,改造体积内平均裂缝长度和等效裂缝条数是滤失量Vl的函数,而滤失量Vl反过来又会影响平均裂缝长度和等效裂缝条数的计算结果,因此须采用迭代求解的方法。

(1)首先选定比较小的初始时间t,假设在该时间段内滤失量Vl=0。

(2)根据滤失量Vl计算该时刻的平均裂缝长度x和等效裂缝条数n。

(3)将计算得到的平均裂缝长度x和等效裂缝条数n代入压裂液滤失模型,计算在该时间段内的滤失量Vl′。

(4)若|Vl′-Vl|<ε,则计算终止,Vl=Vl′;若不满足,Vl=Vl′,重复(2)、(3)。

(5)增加时间步长Δt,根据滤失量Vl计算t+Δt时刻的平均裂缝长度x和等效裂缝条数n。

(6)重复(3)～(5),得出压裂施工结束时改造体积内的平均裂缝长度x和等效裂缝条数n。

改造体积内平均裂缝长度和等效裂缝条数计算流程如图1所示。

有了平均裂缝长度和等效裂缝条数这两个关键参数,就可以用来表征改造体积内裂缝网络的导流能力和裂缝密度。

图1 改造体积内平均裂缝长度和等效裂缝条数计算流程Fig.1 Flow chart for calculating average crack length and number of equivalent cracks in reconstructed volume

3 体积压裂工程改造效果评价模型

3.1 有微地震数据的体积压裂工程改造效果评价模型

体积压裂工程改造效果受到改造体积、裂缝网络导流能力和裂缝密度的综合影响,可以定义体积压裂工程改造效果评价参数为这3个参数的乘积,其值越大代表改造效果越好,有微地震监测数据的体积压裂工程改造效果评价模型可以表示为

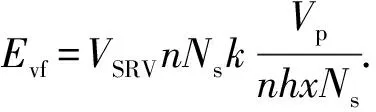
(21)

3.2 无微地震数据的体积压裂工程改造效果评价模型

由于微地震监测改造体积的方法受到观测井位置和生产成本等条件的限制,并不是每口井都能够进行微地震裂缝监测。对于无微地震监测数据的体积压裂作业,无法获取其SRV,但可以用其他能够表征SRV的参数代替。早在2002年Fisher、Maxwell等[9-10]就指出在Barnett页岩压裂改造过程中,压裂规模即注入地层的液体体积与裂缝网络改造体积之间存在良好的正相关性,在同等条件下注入地层的液体体积越大,微地震监测到的SRV就越大,因此对于无微地震监测数据的油气井,可以利用注入地层的液体体积来表征改造体积的大小。则无微地震监测数据的体积压裂工程改造效果评价模型可以表示为

(22)

式中,Vf为全井压裂过程中注入的滑溜水、前置液、携砂液和顶替液的总体积,m3。

4 体积压裂工程改造效果评价模型应用分析

油气井产能主要受储层含油丰度等地质条件和压裂工程改造效果的影响,为了更为准确地反映体积压裂工程改造效果与油气井产能之间的关系,需要选取储层地质条件一致的油气井作为分析对象,从而剔除其对产能的影响,防止产能差异影响因素误判现象的发生,从而更为真实地反映体积压裂工程改造效果与产能之间的关系。为此选取某致密储层地质条件一致的相邻4口水平井作为分析对象,其中Well 1和Well 2位于平台1上,Well 3和Well 4位于平台2上(图2),各井水平间距为300 m,水平延伸方向均为最小水平主应力方向。表1为4口井的完井基本参数,从表1可以看出,4口井具有基本相同的井身结构,井底压力、温度、岩性、含油性、流体黏度、孔隙度、渗透率等储层地质条件一致,微地震监测及初期试采情况均说明各井之间没有产生连通,生产初期不考虑各井之间的相互干扰。由此可知这4口水平井产能的差异不是由地质条件引起的,而是由压裂工程改造效果不同造成的。

表2为该4口水平井的压裂施工参数,4口井在压裂级数、裂缝净压、注液体积、支撑剂体积以及平均注入排量上均有一定的差异,仅仅从压裂施工参数上无法对这4口井的压裂工程改造效果进行评价。

根据本文中建立的模型对这4口水平井体积压裂改造体积内的平均裂缝长度和等效裂缝条数进行计算,然后以此为依据计算体积压裂工程改造效果的评价参数,表3为相应的计算结果及微地震监测数据和压裂后第1年的累积产量。

表1 完井基本参数

表2 压裂施工参数

表3 压裂效果评价参数计算结果及压后第1年累积产量Table 3 Calculation results of evaluation parameters of fracturing effect and cumulative production after the first year of fracturing

图3给出了压裂工程改造效果评价参数与累积产量之间的关系。从图3可以看出,用来表征体积压裂工程改造效果的SRV和注液体积与累积产量之间的相关性均较差,SRV甚至与累积产量之间存在负相关关系,说明单独依靠SRV或注液体积均无法准确地反映体积压裂的工程效果。通过本文中建立的模型得到改造体积内的平均裂缝长度和等效裂缝条数这两个关键参数,能够对改造体积内的裂缝密度和裂缝导流能力进行表征,综合考虑SRV及其内部裂缝密度和导流能力的体积压裂工程改造效果评价参数与累积产量之间存在较好的相关性(图3 (c)),其相关性系数达到了0.89,因此该参数能够更为真实地反映体积压裂的工程效果。同时,考虑没有微地震监测数据的油气井,用注液体积表征改造体积的压裂工程改造效果评价参数与累积产量之间的相关性系数也达到了0.88(图3(d))。有微地震数据的拟合结果和无微地震数据的拟合结果相差极小,从而也验证了本文中提出的综合考虑改造体积、裂缝密度和导流能力评价压裂效果方法的准确性和一致性,但还无法从当前的样本数据来评价出哪种模型更为适用。在实际的应用过程中,对于有微地震监测的油气井,可以采用微地震监测得到的SRV和实际注液体积分别评价,二者相互验证,并从中找出更适用于本区块的评价模型,从而提高评价结果的准确性。

无论有无微地震监测数据,本文中提出的体积压裂工程改造效果评价参数与油气井产能之间的相关性相比SRV和注液体积均有了明显的提高,能够更为准确的对体积压裂的工程效果进行评价。该评价参数可以为体积压裂设计优化提供指导;其评价结果可以作为油气井产能预测的依据;能够更为真实准确地解释各井之间产能差异的原因,区分压裂效果和地质因素对产能控制的不确定性;同时还可以根据油气井产能和压裂工程改造效果对储层地质特征进行重新评价,提高储层空间分布特征和甜点体预测的准确性。在实际应用过程中,对于同一地区的油气井,首先统计体积压裂工程改造效果的评价结果与产能的关系,然后对比分析体积压裂后油气井产能是受工程改造效果的影响还是受储层孔隙度、渗透率、含油丰度等地质条件的影响,最后判断出导致各井间产能差异的因素,实现油气井产能影响因素的有效区分,并以此对储层的空间分布特征和甜点体位置进行更为准确的评价。

图3 体积压裂效果评价参数与累积产量的关系Fig.3 Relationship between evaluation parameters of volume fracturing effect and cumulative production

5 结 论

(1)体积压裂工程改造效果主要受改造体积及其内部裂缝密度和导流能力的影响,由于微地震得出的SRV不能反映改造体积内裂缝的密度和导流能力,因此仅依靠SRV不能真实准确地评价体积压裂的工程改造效果。

(2)根据能量守恒和物质平衡原理,通过变分法建立了改造体积内平均裂缝长度和等效裂缝条数计算模型,得到了用于描述改造体积内裂缝密度和导流能力的关键参数。

(3)综合考虑影响体积压裂工程改造效果的改造体积、裂缝密度以及导流能力,提出了体积压裂工程改造效果评价参数计算模型,该评价参数在有微地震监测井和无微地震监测井中与产能之间均具有较好的相关性,实现了更为准确的体积压裂工程改造效果评价和油气井产能影响因素的有效区分。